c++常用技巧——离散化 （南昌理工ACM集训队）

应用概述

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。
——————百度

你是否因为开数组过大而MLE
你是否因为不知道如何保存数值而WA到底
你是否从入门到放弃
不要担心不要害怕
离散化可以通过映射 将其简化。

• 如果有些数据本身很大，无法在数组中以本身作为自己的下标
• 当数据只与他们的相对大小有关，而与具体是几无关

那么就可以采用离散化来处理数据了
比如：
原数据： 999999, 1 , 24 , 3
离散化处理后： 4 , 1 , 3 , 2

离散化的方法

常用方法

1. 排序
2. 去重
3. 离散化索引

在STL中有三个函数可以帮助我们进行以上操作

• sort函数用来排序，它的使用方法是sort(数组名,数组名+数组长度) ，很常用的函数
• unique函数用来去重， 它的使用方法是 unique(数组名,数组名+数组长度) 它的去重并不是把重复元素删去，而是将重复元素放在数组的末尾。
• lower_bound函数用来离散化索引，它用来找数组中第一个大于或等于目标值的数据的位置，它的使用方法是lower_bound(数组名,数组名+数组长度,目标值)

知道了这几个函数，离散化数据的操作就十分简单了。
我们需要另开一个数组来同时存放所需值，用来排序去重找到索引，再将索引赋值给原数组。

代码模板

	int a[MAXN],n;   //原数组  数组长度
	int b[MAXN],m;   //索引数组 去重后的数组长度
	/*数组赋值操作
	....
	....将两数组同时赋值
	....
	*/
	sort(b,b+n);
	m=unique(b,b+n)-b;
	for(int i=0;i<m;i++)
		a[i]=lower_bound(b,b+m,a[i])-b;
	//离散化完成 进一步根据题意操作

另一种方法

从别人博客学到的: 离散化：两种离散化方式详解.

1. 结构体存放数据和数据下标
2. 对结构体数据进行排序
3. 枚举着放回原数组 下标就是输入的位置，放入的数据是排序后的索引

代码模板

#include 
const int MAXN=10;
using namespace std;
struct node{
    int data,id;
}b[MAXN];
int a[MAXN],n;
bool rule(node x,node y)
{
    return x.data<y.data;
}
int main()
{
    for(int i=0;i<n;i++)
    {
        scanf("%d",&b[i].data);
        b[i].id=i;
    }
    sort(b,b+n,rule);
    for(int i=0;i<n;i++)
        a[b[i].id]=i;
    return 0;
}

例题分析

链接: P1955 [NOI2015]程序自动分析.

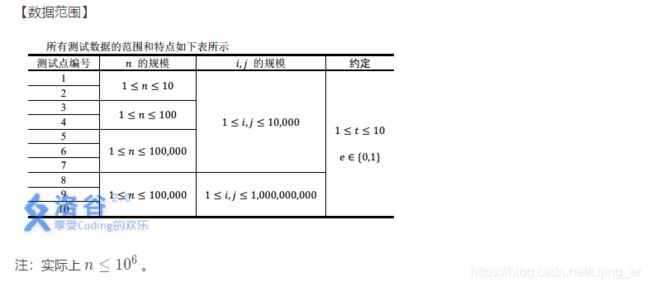
题目分析

• 数据范围很大，但是n在可接受范围内
• 操作与相对大小有关，与具体是几无关

这数据妥妥的要离散化了，不过还需要一些并查集的知识。

AC代码

#include 
using namespace std;
int t,n,ans,k,f[1000005],a[3*1000005],cnt,m;
struct node
{
    int x,y,e;
}r[1000005];

bool rule(node a,node b)
{
    return a.e>b.e;     //合并的操作排在前
}
int find(int x)
{
    if(f[x]==x) return x;
    return f[x]=find(f[x]);
}

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        memset(a,0,sizeof(a));
        memset(r,0,sizeof(r));
        memset(f,0,sizeof(f));
        cnt=-1,ans=1;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d%d",&r[i].x,&r[i].y,&r[i].e); 
            a[++cnt]=r[i].x;
            a[++cnt]=r[i].y;
        }
        sort(a,a+cnt);
        m=unique(a,a+cnt)-a;
        for(int i=0;i<=m;i++)
            f[i]=i;
        for(int i=1;i<=n;i++)
        {
            r[i].x=lower_bound(a,a+m,r[i].x)-a;
            r[i].y=lower_bound(a,a+m,r[i].y)-a;
        }
        sort(r+1,r+1+n,rule);
        for(int i=1;i<=n;i++)
        {
            int x=find(r[i].x);
            int y=find(r[i].y);
            if(r[i].e==1)
                f[x]=y;
            else{
                if(x==y)
                {
                    printf("NO\n");
                    ans=0;
                    break;
                }
            }
        }
        if(ans) printf("YES\n");
    }
    return 0;
}