Python实现蒙特卡罗方法仿真模拟求解圆周率Pi值

       最近遇上了需要仿真模拟采样相关的工作，之前接触过比较牛的方法之一就是蒙特卡罗方法，对于这个随机采样方法的了解过，但是详细的概念什么的早已记不住了，这里给出来百度百科的定义：

蒙特·卡罗方法简介
蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在金融工程学，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域应用广泛。


提出
蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法，为它蒙上了一层神秘色彩。在这之前，蒙特卡罗方法就已经存在。1777年，法国数学家布丰（Georges Louis Leclere de Buffon，1707—1788）提出用投针实验的方法求圆周率π。这被认为是蒙特卡罗方法的起源。

      想了解更多内容的可以参考这里。

     今天通过一个实际的应用来更加清晰地了解一下这个采样方法，就是求解圆周率Pi，这个网上也有很多的相关的实现，实现本身很简单没有什么难度，主要就是想通过实践熟悉方法，具体实现如下：

#!usr/bin/env python
# encoding:utf-8
from __future__ import division


"""
__Author__:沂水寒城
功能： Python基于蒙特卡洛方法实现求解圆周率

计算思想：
在边长为n的正方形里面绘制一个内切圆，此时正方形面积为：n*n,圆形面积为：pi*(n/2)*(n/2)=pi*n*n/4
理论计算来说：内切圆与正方形的面积比为：4/pi:1
用概率论的思想来解释的话：
随机往正方形区域里面点点的话，如果次数足够多，那么点落在圆形区域里面的概率与落在正方形区域里面的概率比为：4/pi:1
"""



import math
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle


def MTKL(num=100000,n=100,pic_path='1000.png'):
    '''
    蒙特卡洛方法
    num:点的数量
    n:正方形边长
    '''
    r=n/2
    #从正方形左下角定点开始顺时针得到四个顶点的坐标
    x1,y1=0,0
    x2,y2=0,n
    x3,y3,=n,n
    x4,y4=n,0
    #圆心坐标
    xr,xy=int((x1+x4)/2),int((y1+y2)/2)
    print 'xr: ',xr
    #绘制正方形区域
    fig=plt.figure()
    ax=fig.add_subplot(111)
    plt.plot([x1,y1],[x2,y2],color='g')
    plt.plot([x2,y2],[x3,y3],color='g')
    plt.plot([x3,y3],[x4,y4],color='g')
    plt.plot([x4,y4],[x1,y1],color='g')
    #随机丢点
    posX=np.random.uniform(0,n,num)
    posY=np.random.uniform(0,n,num)
    #计算点到圆心的距离
    dis=np.sqrt((posX-xr)**2 + (posY-xy)**2)
    #统计落在圆内点的数目
    res=sum(np.where(dis<=r,1,0))
    #计算pi的近似值（Monte Carlo:用统计值去近似真实值）
    pi=4*res/num
    plt.plot(posX,posY,'bo',markersize=0.4)
    plt.axis('equal') #防止图像变形
    circle=Circle(xy=(xr,xy),radius=r,alpha=0.5)
    ax.add_patch(circle)
    plt.title('PI: '+str(pi))
    plt.savefig(pic_path)
    plt.show()


if __name__=='__main__':
    MTKL(num=10,n=100,pic_path='10.png')
    MTKL(num=100,n=100,pic_path='100.png')
    MTKL(num=1000,n=100,pic_path='1000.png')
    MTKL(num=10000,n=100,pic_path='10000.png')
    MTKL(num=100000,n=100,pic_path='100000.png')
    MTKL(num=1000000,n=100,pic_path='1000000.png')
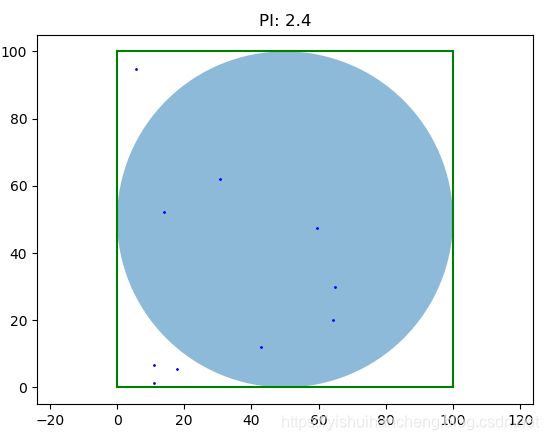
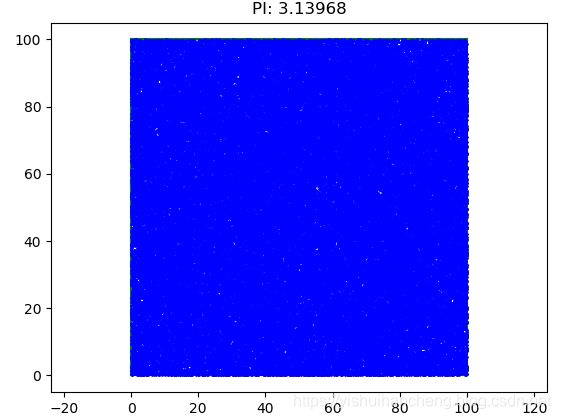
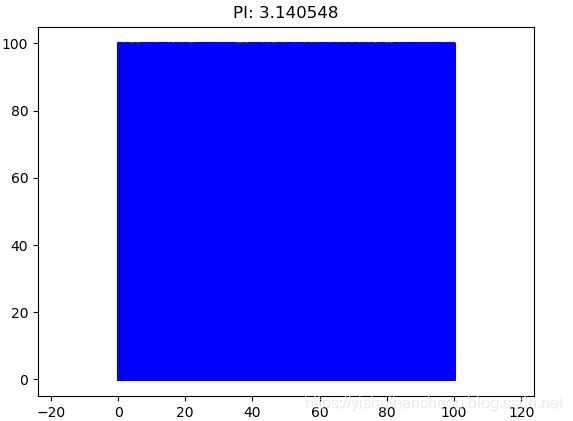
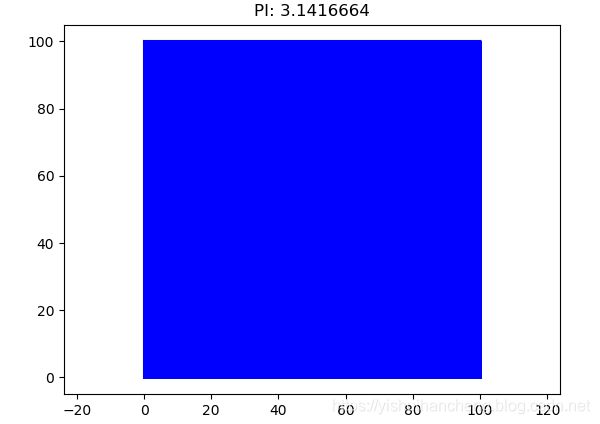
    MTKL(num=10000000,n=100,pic_path='10000000.png')

      整体的代码很简单，详细的注释也都添加了，我们实验了不同的次数来观察圆周率求解的精度，理论上来说：随着实验次数的增加，精度会越来越准确，下面简单看一下结果：

num=10

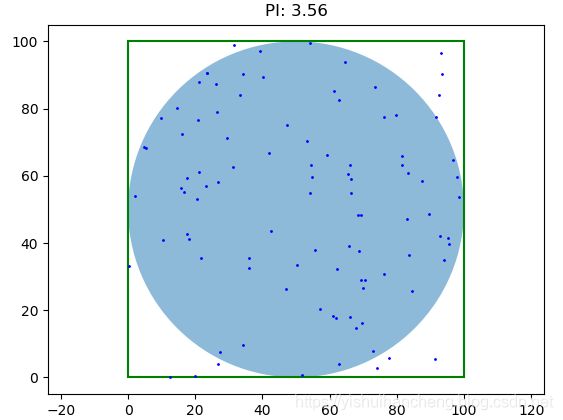
num=100

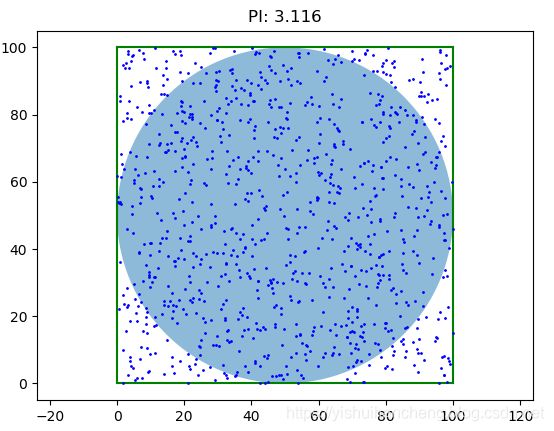
num=1000

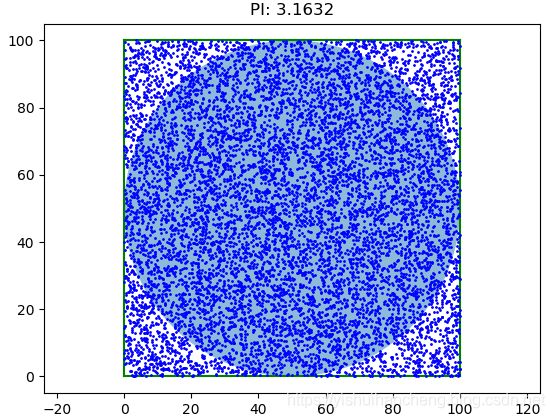
num=10000

num=100000

num=1000000

num=10000000

    我们设置的实验从10个点到1千万个点，可以直观地看到：随着点数量的增加，圆周率Pi的计算精度也随之升高。