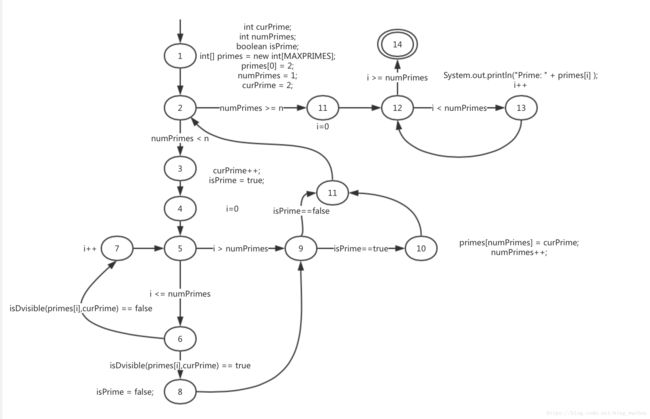
点覆盖、边覆盖、主路径覆盖的一个实例

题目：

private static void printPrimes(int n) {
    int curPrime; //Value currently considered for primeness
    int numPrimes; // Number of primes found so far;
    boolean isPrime; //Is curPrime prime?
    int[] primes = new int[MAXPRIMES];// The list of primes.

    // Initialize 2 into the list of primes.
    primes[0] = 2;
    numPrimes = 1;
    curPrime = 2;
    while(numPrimes < n) {
        curPrime++; // next number to consider...
        isPrime = true;
        for(int i = 0; i <= numPrimes; i++ ) {//for each previous prime.
            if(isDvisible(primes[i],curPrime)) {//Found a divisor, curPrime is not prime.
                isPrime = false;
                break;
            }
        }
        if(isPrime) {// save it!
            primes[numPrimes] = curPrime;
            numPrimes++;
        }
    }// End while
    for(int i = 0; i < numPrimes; i++) {// print all the primes out
        System.out.println("Prime: " + primes[i] );
    }
}

1. Draw the control flow graph for the printPrime() method
   

2. Consider test cases ti = (n = 3) and t2 = ( n = 5). Although these tour the same prime paths in printPrime(), they don’t necessarily find the same faults. Design a simple fault that t2 would be more likely to discover than t1 would.
   while(numPrimes < n) -> while(numPrimes < 4)

3. For printPrime(), find a test case such that the corresponding test path visits the edge that connects the beginning of the while statement to the for statement without going through the body of the while loop.
   printPrimes(1)

4. Enumerate the test requirements (Tr) for node coverage, edge coverage, and prime path coverage for the path for printPrimes().
   点覆盖：
   [1,2,3,4,5,6,7,8,9,10,11,12,13,14] [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 ]
   边覆盖：
   

   [(1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,5),(6,8),(8,9),(5,9),(9,10),(9,2),(10,2),(2,11),(11,12),(12,13),(12,14),(13,12)] [ ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 5 , 6 ) , ( 6 , 7 ) , ( 7 , 5 ) , ( 6 , 8 ) , ( 8 , 9 ) , ( 5 , 9 ) , ( 9 , 10 ) , ( 9 , 2 ) , ( 10 , 2 ) , ( 2 , 11 ) , ( 11 , 12 ) , ( 12 , 13 ) , ( 12 , 14 ) , ( 13 , 12 ) ]
   
   主路径覆盖：
   [1,2,3,4,5,6,7] [ 1 , 2 , 3 , 4 , 5 , 6 , 7 ]
   [1,2,3,4,5,9,10] [ 1 , 2 , 3 , 4 , 5 , 9 , 10 ]
   [1,2,3,4,5,6,8,9,10] [ 1 , 2 , 3 , 4 , 5 , 6 , 8 , 9 , 10 ]
   [1,2,11,12,13] [ 1 , 2 , 11 , 12 , 13 ]
   [1,2,11,12,14] [ 1 , 2 , 11 , 12 , 14 ]

   [2,3,4,5,6,8,9,2] [ 2 , 3 , 4 , 5 , 6 , 8 , 9 , 2 ]
   [2,3,4,5,6,8,9,10,2] [ 2 , 3 , 4 , 5 , 6 , 8 , 9 , 10 , 2 ]
   [2,3,4,5,9,2] [ 2 , 3 , 4 , 5 , 9 , 2 ]
   [2,3,4,5,9,10,2] [ 2 , 3 , 4 , 5 , 9 , 10 , 2 ]

   [3,4,5,6,8,9,2,11,12,13] [ 3 , 4 , 5 , 6 , 8 , 9 , 2 , 11 , 12 , 13 ]
   [3,4,5,6,8,9,2,11,12,14] [ 3 , 4 , 5 , 6 , 8 , 9 , 2 , 11 , 12 , 14 ]
   [3,4,5,6,8,9,10,2,11,12,13] [ 3 , 4 , 5 , 6 , 8 , 9 , 10 , 2 , 11 , 12 , 13 ]
   [3,4,5,6,8,9,10,2,11,12,14] [ 3 , 4 , 5 , 6 , 8 , 9 , 10 , 2 , 11 , 12 , 14 ]
   [3,4,5,9,2,11,12,13] [ 3 , 4 , 5 , 9 , 2 , 11 , 12 , 13 ]
   [3,4,5,9,2,11,12,14] [ 3 , 4 , 5 , 9 , 2 , 11 , 12 , 14 ]
   [3,4,5,9,10,2,11,12,13] [ 3 , 4 , 5 , 9 , 10 , 2 , 11 , 12 , 13 ]
   [3,4,5,9,10,2,11,12,14] [ 3 , 4 , 5 , 9 , 10 , 2 , 11 , 12 , 14 ]

   [4,5,6,8,9,2,3,4] [ 4 , 5 , 6 , 8 , 9 , 2 , 3 , 4 ]
   [4,5,6,8,9,10,2,3,4] [ 4 , 5 , 6 , 8 , 9 , 10 , 2 , 3 , 4 ]

   [5,6,7,5] [ 5 , 6 , 7 , 5 ]
   [5,6,8,9,2,3,4,5] [ 5 , 6 , 8 , 9 , 2 , 3 , 4 , 5 ]
   [5,6,8,9,10,2,3,4,5] [ 5 , 6 , 8 , 9 , 10 , 2 , 3 , 4 , 5 ]

   [6,7,5,6] [ 6 , 7 , 5 , 6 ]
   [6,7,5,9,2,3,4] [ 6 , 7 , 5 , 9 , 2 , 3 , 4 ]
   [6,7,5,9,10,2,3,4] [ 6 , 7 , 5 , 9 , 10 , 2 , 3 , 4 ]
   [6,8,9,2,3,4,5,6] [ 6 , 8 , 9 , 2 , 3 , 4 , 5 , 6 ]
   [6,8,9,10,2,3,4,5,6] [ 6 , 8 , 9 , 10 , 2 , 3 , 4 , 5 , 6 ]

   [7,5,6,7] [ 7 , 5 , 6 , 7 ]
   [7,5,9,2,11,12,13] [ 7 , 5 , 9 , 2 , 11 , 12 , 13 ]
   [7,5,9,2,11,12,14] [ 7 , 5 , 9 , 2 , 11 , 12 , 14 ]
   [7,5,9,10,2,11,12,13] [ 7 , 5 , 9 , 10 , 2 , 11 , 12 , 13 ]
   [7,5,9,10,2,11,12,14] [ 7 , 5 , 9 , 10 , 2 , 11 , 12 , 14 ]
   [7,5,6,8,9,2,3,4,] [ 7 , 5 , 6 , 8 , 9 , 2 , 3 , 4 , ]
   [7,5,6,8,9,10,2,3,4] [ 7 , 5 , 6 , 8 , 9 , 10 , 2 , 3 , 4 ]
   [7,5,6,8,9,2,11,12,13] [ 7 , 5 , 6 , 8 , 9 , 2 , 11 , 12 , 13 ]
   [7,5,6,8,9,2,11,12,14] [ 7 , 5 , 6 , 8 , 9 , 2 , 11 , 12 , 14 ]
   [7,5,6,8,9,10,11,12,13] [ 7 , 5 , 6 , 8 , 9 , 10 , 11 , 12 , 13 ]
   [7,5,6,8,9,10,11,12,14] [ 7 , 5 , 6 , 8 , 9 , 10 , 11 , 12 , 14 ]

   [8,9,2,3,4,5,6,8] [ 8 , 9 , 2 , 3 , 4 , 5 , 6 , 8 ]
   [8,9,10,2,3,4,5,6,8] [ 8 , 9 , 10 , 2 , 3 , 4 , 5 , 6 , 8 ]
   [8,9,2,3,4,5,6,7] [ 8 , 9 , 2 , 3 , 4 , 5 , 6 , 7 ]
   [8,9,10,2,3,4,5,6,7] [ 8 , 9 , 10 , 2 , 3 , 4 , 5 , 6 , 7 ]

   [9,2,3,4,5,9] [ 9 , 2 , 3 , 4 , 5 , 9 ]
   [9,10,2,3,4,5,9] [ 9 , 10 , 2 , 3 , 4 , 5 , 9 ]
   [9,2,3,4,5,6,8,9] [ 9 , 2 , 3 , 4 , 5 , 6 , 8 , 9 ]
   [9,10,2,3,4,5,6,8,9] [ 9 , 10 , 2 , 3 , 4 , 5 , 6 , 8 , 9 ]

   [10,2,3,4,5,6,8,9,10] [ 10 , 2 , 3 , 4 , 5 , 6 , 8 , 9 , 10 ]

   [12,13,12] [ 12 , 13 , 12 ]

   [13,12,14] [ 13 , 12 , 14 ]

累死我了，，应该是这些吧。。。

2018.3.26

突然被告诉说我的图里出现了两个11号。。。好吧，画图的时候失误了一下。。
9和10是直接连到2的
把我的草稿上传一下好了。。