LeetCode中二叉树相关题

Leetcode中二叉树相关题

二叉树相关的题相对来说还是比较简单的，都是套路

第一题：求二叉树中最大路径和

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

       1
      / \
     2   3

输出: 6

示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

这就是个后序遍历嘛

int ans = INT_MIN;
int oneSideMax(TreeNode* root) {
	if (root == nullptr) return 0;
	int left = max(0, oneSideMax(root->left));
	int right = max(0, oneSideMax(root->right));
	ans = max(ans, left + right + root->val);
	return max(left, right) + root->val;
}

C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int sum = INT_MIN;

    int maxPathSumchild(TreeNode* root)
    {
        //递归出口
        if(root == nullptr)
        {
            return 0;
        }

        //递归求 某个节点 的 左子树 和 右子树 的权值
        int left = max(0,maxPathSumchild(root->left));
        int right = max(0,maxPathSumchild(root->right));

        //检查是否需要更新创建新的路径，新路径的权值是left + right + root->val，最后更新sum
        sum = max(sum,(left + right + root->val));
        
        //递归返回 到当前节点的一条最大路径
        return max(left,right) + root->val;
    }
    int maxPathSum(TreeNode* root)
    {
        maxPathSumchild(root);
        return sum;
    }
};

第二题：根据前序遍历和中序遍历的结果还原⼀棵⼆叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7
 

限制：

• 0 <= 节点个数 <= 5000

直接看代码：

TreeNode buildTree(int[] preorder, int preStart, int preEnd,int[] inorder, int inStart, int inEnd, Map<Integer, Integer> inMap) {
	if(preStart > preEnd || inStart > inEnd) 
		return null;
		
	TreeNode root = new TreeNode(preorder[preStart]);
	
	int inRoot = inMap.get(root.val);
	int numsLeft = inRoot - inStart;
	
	root.left = buildTree(preorder, preStart + 1, preStart + numsLeft,
						inorder, inStart, inRoot - 1, inMap);
	root.right = buildTree(preorder, preStart + numsLeft + 1, preEnd,
						inorder, inRoot + 1, inEnd, inMap);
	return root;
}

这道题不难，看上一个例子就知道基本思想，重点是边界控制问题

根据下面9张图看一下例子当中二叉树的构建过程

2.

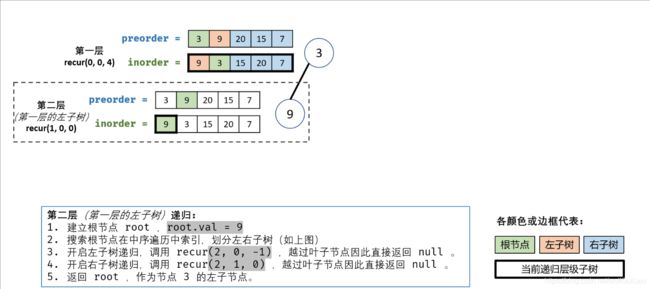
3.

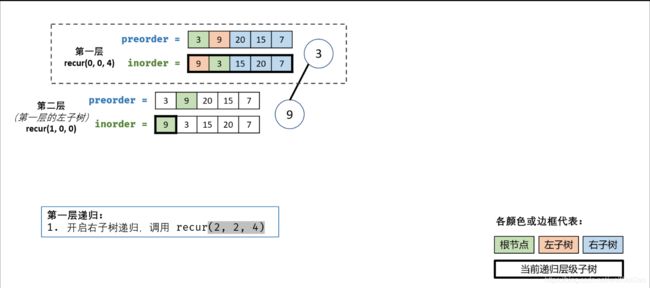
4.

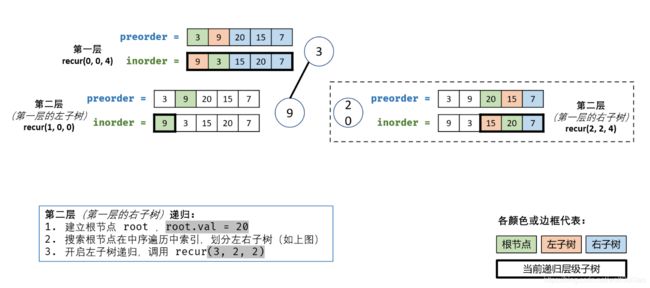
5.

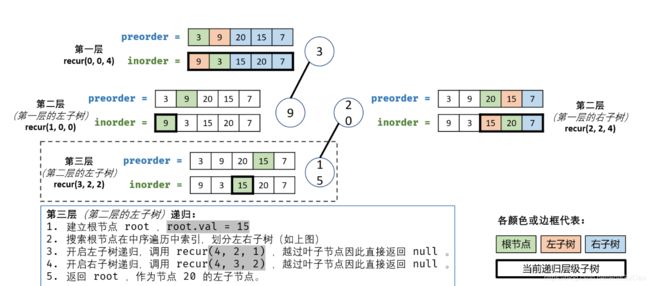
6.

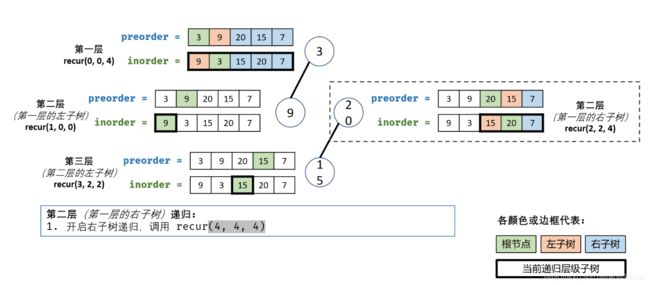
7.

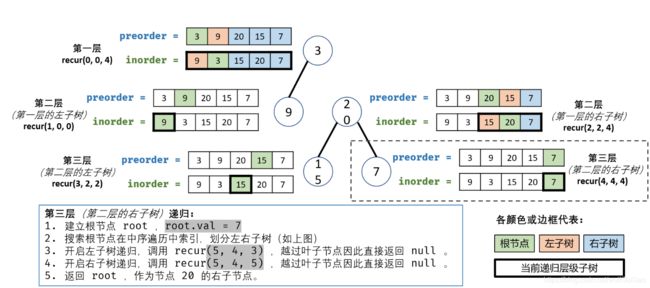
8.

9.

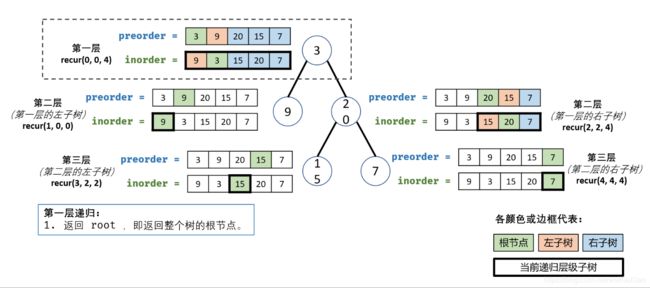
C++代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        //递归分治
        //控制好边界，剩下的交给递归
        return recursionBuild(preorder.begin(),preorder.end(),
                                inorder.begin(),inorder.end());
    }

    //递归分治
    TreeNode* recursionBuild(vector<int>::iterator preBegin, vector<int>::iterator preEnd,                              vector<int>::iterator inBegin, vector<int>::iterator inEnd )
    {
        if(inEnd==inBegin) 
            return NULL;

        TreeNode* cur = new TreeNode(*preBegin);

        //在中序遍历数组中找前序遍历的第一个节点，最为中序数组的左右子树分界点
        auto root = find(inBegin,inEnd,*preBegin);

        //递归构造左右子树
        cur->left = recursionBuild(preBegin + 1,preBegin + (root - inBegin) + 1,
                                                inBegin,root);
        cur->right = recursionBuild(preBegin + 1 + (root - inBegin),preEnd,
                                                root + 1,inEnd);

        return cur;
    }
};

第三题：恢复⼀棵 BST

二叉搜索树中的两个节点被错误地交换。

请在不改变其结构的情况下，恢复这棵树。

示例 1:

输入: [1,3,null,null,2]

   1
  /
 3
  \
   2

输出: [3,1,null,null,2]

   3
  /
 1
  \
   2

示例 2:

输入: [3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

输出: [2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

这道题难点,是找到那两个交换节点,把它交换过来就行了.

这里我们二叉树搜索树的中序遍历(中序遍历遍历元素是递增的)

如下图所示, 中序遍历顺序是 4,2,3,1,我们只要找到节点4和节点1交换顺序即可!

这里我们有个规律发现这两个节点:

第一个节点,是第一个按照中序遍历时候前一个节点大于后一个节点,我们选取前一个节点,这里指节点4;

第二个节点,是在第一个节点找到之后, 后面出现前一个节点大于后一个节点,我们选择后一个节点,这里指节点1;

void traverse(TreeNode* node) {
	if (!node) return;
	
	traverse(node->left);
	
	if (node->val < prev->val) {
		s = (s == NULL) ? prev : s;
		t = node;
	}
	prev = node;
	
	traverse(node->right);
}

first记录第一个被错误交换的节点指针，second记录第二个被错误交换的节点指针，prev记录在中序遍历中上一个被遍历到的节点指针；

通过比较当前节点的值和上一个节点的值来判断其是否是first或者second；注意：若被错误交换的两个节点在中序遍历中是相邻的两个节点（相邻是指以相邻的顺序被遍历到），与不相邻的区别；

完整代码：

class Solution {
private:
    TreeNode* first = nullptr;//指向第一个错误的节点
    TreeNode* second = nullptr;//指向第二个错误的节点
    TreeNode* pre = new TreeNode(INT_MIN);//相对于当前节点在中序遍历下的上一个节点

    void helper(TreeNode* root)
    {
        if(root == nullptr)
        {
            return;
        }

        //中序遍历
        helper(root->left);

        //注意全程只有两个错误节点，所以下面的代码才可以那样写
        //找到第一个节点才可以继续找第二个错误节点，但是注意这两个节点并不一定是相邻的
        if(first == nullptr && pre->val > root->val)
        {
            first = pre;
        }

        if(first != nullptr && pre->val > root->val)
        {
            second = root;
        }
        
        pre = root;

        helper(root->right);
    }
public:
    void recoverTree(TreeNode* root) 
    {
        helper(root);

        swap(first->val,second->val);
    }
    
};

最后发现这不就是个中序遍历嘛，

你看， Hard 难度的题⽬不过如此， ⽽且还这么有规律可循， 只要把框架写出来， 然后往相应的位置加东⻄就⾏了， 这不就是思路吗