数据结构与算法 & 二叉树工具
二叉树
- 一、二叉树
- 1.定义(百度):
- 2.二叉树的特点
- 二、二叉树的生成
- 1.二叉树数据结构实现
- 2.二叉树数据的表示
- 3.二叉树生成
- 三、二叉树遍历与获得树高
- 1.二叉树遍历
- 2.二叉树获得树高
- 四、总结
一、二叉树
1.定义(百度):
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
2.二叉树的特点
二叉的分类很多,特性也不少。这里不准备细说。
1)二叉树只有一个根节点
2)二叉树的每个节点会有两个孩子。分为左孩子、右孩子。两个还是不一定必须拥有。
二、二叉树的生成
1.二叉树数据结构实现
二叉树可以看成每个节点的组成,那么这个节点要有存储数据的地方,要有指向左右孩子的指针。
所以可以这样生成:
typedef struct B_TREE {
USER_TYPE data;//用户自定义数据类型
struct B_TREE *left;//指向左孩子
struct B_TREE *right;//指向右孩子
}B_TREE;
2.二叉树数据的表示
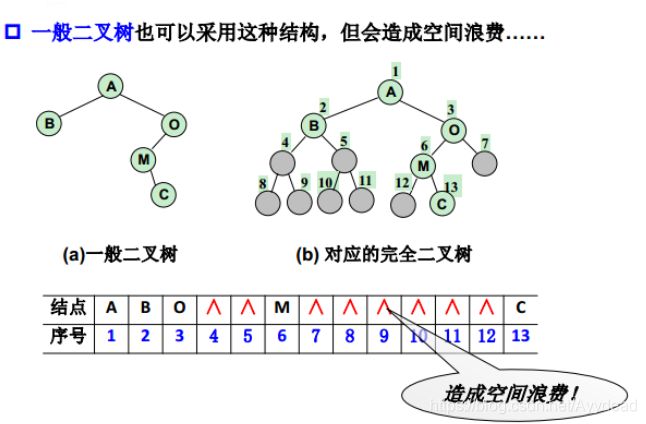
- 给每个节点标上序号,但是需要完全二叉树才能将每个节点位置表示清楚。所以容易造成空间浪费。
2. 父节点(左孩子,右孩子)模式
上面的二叉可以这样表述为: A(B, O(M( ,C))
这种方式比较节省空间,但是也让处理该二叉树麻烦起来。因为我们加入了左右括号和逗号,使得识别难度增加了。
该模式有 “字符”,‘’左括号‘,“右括号”,“逗号”’
接下来分析一下该模式的各个状态:

最后我们生成一个自动状态变迁图。

依照这个图我们开始编码:
#define B_TREE_STATUS_START 1 //开始状态
#define B_TREE_STATUS_ROOT 2 //根状态
#define B_TREE_STATUS_LEFTBRACKET 3 //左括号状态
#define B_TREE_STATUS_RIGHTBRACKET 4 //右括号状态
#define B_TREE_STATUS_ALPHA 5 //字母状态
#define B_TREE_STATUS_COMMA 6 //逗号状态
#define B_TREE_STATUS_END 7 //结束状态
状态的判定:
while (arg.ok && !arg.finished) {
arg.index += skipBlank(str + arg.index);//跳过空格
switch (arg.status) {
case B_TREE_STATUS_START:
dealBTreeStart(&arg, str[arg.index]);
break;
case B_TREE_STATUS_ROOT:
dealBTreeRoot(&arg, str[arg.index]);
break;
case B_TREE_STATUS_LEFTBRACKET:
dealBTreeLeftbracket(&arg, str[arg.index]);
break;
case B_TREE_STATUS_RIGHTBRACKET:
dealBTreeRightbracket(&arg, str[arg.index]);
break;
case B_TREE_STATUS_ALPHA:
dealBTreeAlpha(&arg, str[arg.index]);
break;
case B_TREE_STATUS_COMMA:
dealBTreeComma(&arg, str[arg.index]);
break;
case B_TREE_STATUS_END:
if (arg.bracketMatch != 0) {
errMess = "括号不匹配!";
arg.ok = FALSE;
break; // 这个break;用来跳出switch
// 这个break;不是用来结束循环的!
}
*root = arg.root;
arg.finished = TRUE;
break;
default:
break;
}
}
状态的转换:
//开始状态
static void dealBTreeStart(B_TREE_ARG *arg, int ch) {
if (isalpha(ch)) {
dealRoot(arg, ch);//进入根状态
} else {
errMess = "不能是空树!";
arg->ok = FALSE;//错误
}
}
//解决根状态
static void dealRoot(B_TREE_ARG *arg, int ch) {
arg->node = arg->root = createNode(ch);
arg->status = B_TREE_STATUS_ROOT;//转换到根状态,记录下来。
arg->index++;//为判断下个字符检测
}
基本思路: 原状态(已知) --> 判断字符类型 – > 处理该字符 --> 转换原状态 --> 进入下一个字符
其它各状态略!
3.二叉树生成
从上面的自动转态变迁图,我们知道了如何处理用户给予的二叉树数据表达形式。那么我们怎么生成二叉树呢?
二叉树难的地方就是,怎么将各个节点连接起来?谁是左孩子?谁是右孩子?
A(B(D(F, G), J(, L(K, ))), C(E(H,I)))
观察这个你发现了啥?
1.区别左右孩子的标志是“逗号”。逗号后面的数据一定是右孩子。
2.字符后面的有左括号,那么该字符一定有孩子。
那么怎么确认每个节点的父节点呢?
我们这里采用堆栈空间存储每个父节点。
A,是父节点,入栈,B是父节点,入栈,D是父节点,入栈;当前栈内: 底,ABD,顶
G是右孩子,且后面是右括号,父节点D出栈;当前栈内: 底,AB,顶
J是父节点,入栈,L是父节点,入栈;当前栈内: 底,ABJL,顶
L孩子遍历结束,出栈,J孩子遍历结束,出栈,B孩子遍历结束,出栈;当前栈内: 底,A,顶
…
就这样,实现父节点的寻找。尤其我们创造过一种堆栈工具。正好可以使用。数据结构与算法 & 堆栈工具
再结合上述发现,就能很好生成一个二叉树了。
static B_TREE *createNode(int ch) {
B_TREE *node = NULL;
node = (B_TREE *) calloc(sizeof(B_TREE), 1);
// 为了节省时间,这里不处理申请空间失败的问题。
node->data = ch;
node->left = node->right = NULL;
return node;
}
static void dealNode(B_TREE_ARG *arg, int ch) {
B_TREE *parent;
arg->node = createNode(ch);
// 找到其父节点,将node置位父的左、右孩子
parent = (B_TREE *) readTop(arg->stack);
if (LEFT_CHILD == arg->whichChild) {
parent->left = arg->node;
} else {
if (NULL != parent->right) {
free(arg->node);
errMess = "二叉树不存在第三个子节点!";
arg->ok = FALSE;
return;
}
parent->right = arg->node;
}
arg->status = B_TREE_STATUS_ALPHA;
arg->index++;
}
注意: 这里有一个堆栈空间的容量申请问题。
可以简单处理为用户输入数据长度;也可以遍历字符,找到括号匹配数目,确定容量。
三、二叉树遍历与获得树高
1.二叉树遍历
- 先根序遍历 :根,左孩子,右孩子
- 中根序遍历:左孩子, 根,右孩子
- 后根序遍历 :左孩子,右孩子, 根
简单来说,就是将二叉树看成一个多个左右子二叉树组合。
实现思路:就是递归了。
简单介绍先根序,代码如下:
//先根遍历
void firstRootVisit(const B_TREE *root) {
if (NULL == root) {
return;
}
printf("%c ", root->data);
firstRootVisit(root->left);
firstRootVisit(root->right);
}
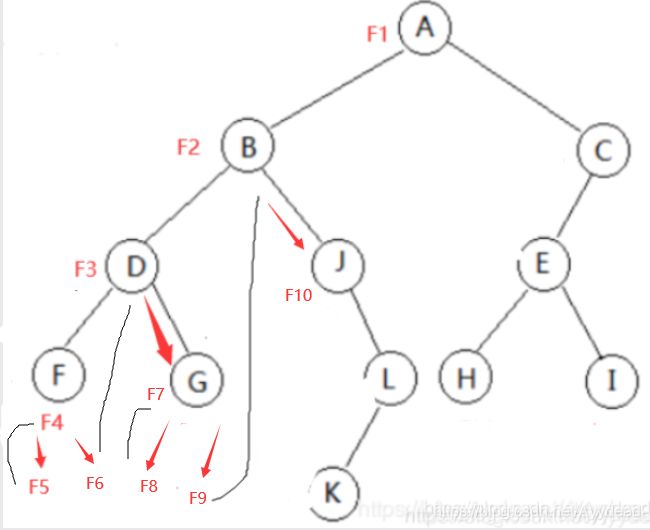
F1,输出A,向左孩子走;调用F2,输出B,向左孩子走;调用F3,输出D,向左孩子走;调用F4,输出F,向左孩子走;
调用F5,root 为0,(黑线),退回到F4,向右孩子走;调用F6,root 为0,(黑线),退回到F3,
向右孩子走;调用F7,输出G,等等
//中根遍历
void middleRootVisit(const B_TREE *root) {
if (NULL == root) {
return;
}
middleRootVisit(root->left);
printf("%c ", root->data);
middleRootVisit(root->right);
}
//后跟遍历
void lastRootVisit(const B_TREE *root) {
if (NULL == root) {
return;
}
lastRootVisit(root->left);
lastRootVisit(root->right);
printf("%c ", root->data);
}
2.二叉树获得树高
基本思路:
1.遍历
2.记录当前递归深度。
3.比较每次最深深度
4.返回最深深度
我们知道,递归调用时,每调用一次,是深入一层,返回时仍是当初深度。但是如何比较每次深入的最大深度呢?
使用静态存储变量。
//树深
static int treeDeep(const B_TREE *root, int level) {
static int maxLevel = 0;//保存最大深度
if (root == NULL) {
return maxLevel;//结束
}
maxLevel = maxLevel < level ? level : maxLevel;//当前深度和最大深度比较
treeDeep(root->left, level + 1);//向左孩子方向,进入下一深度
treeDeep(root->right, level + 1);//向右孩子方向,进入下一深度
return maxLevel;
}
//最大数深
int getTreeDeep(const B_TREE *root) {
return treeDeep(root, 1);
}
四、总结
1.编程需要考虑长远性。工具终会使用。
2.递归很巧妙。一定要多分析,从而掌握。
3.灵活多变,不拘泥·。
笔者水平有限,目前只能描述以上问题,如果有其他情况,可以留言,有错误,请指教,有继续优化的,请分享,谢谢!
本篇文章是否有所收获?阅读是否舒服?又什么改进建议?希望可以给我留言或私信,您的的分享,就是我的进步。谢谢。
完整代码有点长,准备弄个文档。或链接。
2020年03.18 家
