NFA转DFA的子集构造(Subset Construction)算法详解
NFA转DFA的子集构造Subset Construction算法
- 1 概念
- 1.1 虎书概念
- 1.2 龙书概念
- 2 举个例子解释
- 3 如何最小化DFA的状态数量
- 4 总结
之前学习编译原理的时候老师有讲过子集构造法,当时我以为自己听懂了,信心满满。可是这两天我做了一些题目,发现自己实际上还是太嫩了,学习浮于表面。之后又重新看了龙书和虎书,对子集构造法有了更深层次的了解。特此发出一篇文章分享我的经验。
1 概念
概念是我们学习编译原理的重中之重,虽然他很晦涩难懂,但我有必要将其放在最开始。
1.1 虎书概念
虎书的概念更偏向于理论化,我当时看的时候一头雾水,但是不要担心,之后会一点一点解释的。
首先,我们形式化定义 ϵ \epsilon ϵ闭包如下:
- e d g e ( s , c ) edge(s,c) edge(s,c):状态 s s s沿着标有 c c c的边可到达的所有NFA状态的集合;
- c l o s u r e ( S ) closure(S) closure(S): 对于状态集合 S S S,从 S S S出发,只通过 ϵ \epsilon ϵ边可以达到的状态集合;
- 这种经过 ϵ \epsilon ϵ边的概念可以用数学方法表述,即 c l o s u r e ( S ) closure(S) closure(S)是满足如下条件的最小集合 T T T:
T = S ∪ ( ⋃ s ∈ T e d g e ( s , ϵ ) ) T=S \cup \left( \bigcup_{s \in T}edge(s,\epsilon) \right) T=S∪(⋃s∈Tedge(s,ϵ)) - 我们可以用迭代法来算出 T T T:
T ← S r e p e a t T ′ ← T T ← T ′ ∪ ( ⋃ s ∈ T ′ e d g e ( s , ϵ ) ) u n t i l T = T ′ T \leftarrow S \\ repeat \ T' \leftarrow T \\ \qquad \quad T \leftarrow T' \cup \left( \bigcup_{s \in T'}edge(s,\epsilon) \right) \\ until \ T=T' T←Srepeat T′←TT←T′∪(⋃s∈T′edge(s,ϵ))until T=T′
- 这种经过 ϵ \epsilon ϵ边的概念可以用数学方法表述,即 c l o s u r e ( S ) closure(S) closure(S)是满足如下条件的最小集合 T T T:
解释一下:当我们位于一个状态集合 S S S, S S S里任意状态经过若干 ϵ \epsilon ϵ能够到达的状态,都将包含在 c l o s u r e ( S ) closure(S) closure(S) 里。
- 龙书里将这个操作定义为 ϵ − c l o s u r e ( T ) \epsilon-closure(T) ϵ−closure(T)( T T T为状态集合)。
现在,假设我们位于由NFA状态 s i , s k , s l s_i,s_k,s_l si,sk,sl组成的集合 d = { s i , s k , s l } d= \lbrace s_i,s_k,s_l \rbrace d={si,sk,sl}中。从 d d d中的状态出发,输入符号 c c c,将到达NFA新的状态集;我们称这个状态集为 D F A e d g e ( d , c ) DFAedge(d,c) DFAedge(d,c):
- D F A e d g e ( d , c ) = c l o s u r e ( ⋃ s ∈ d e d g e ( s , c ) ) DFAedge(d,c)=closure \left( \bigcup_{s \in d}edge(s,c) \right) DFAedge(d,c)=closure(⋃s∈dedge(s,c))
解释一下:将遍历集合 d d d中的所有状态,得到 d d d 关于 T = e d g e ( s , c ) T=edge(s,c) T=edge(s,c)的状态集,并对 T T T 求 c l o s u r e ( T ) closure(T) closure(T),得到的即为 D F A e d g e ( d , c ) DFAedge(d,c) DFAedge(d,c)。简而言之,就是从一个状态集,经过一个输入到达的状态集为 T ′ = D F A e d g e ( d , c ) T'=DFAedge(d,c) T′=DFAedge(d,c)。
利用 D F A e d g e DFAedge DFAedge能更形式化地写出NFA模拟算法。如果初态是 s 1 s_1 s1,输入字符串是 c 1 , . . . , c k c_1,...,c_k c1,...,ck,则算法为:
- d ← c l o s u r e ( { s 1 } ) f o r i ← 1 t o k d ← D F A e d g e ( d , c i ) d \leftarrow closure( \lbrace s_1 \rbrace ) \\ for \ i \leftarrow 1 \ to \ k \\ \quad d \leftarrow DFAedge(d,c_i) d←closure({s1})for i←1 to kd←DFAedge(d,ci)
有了 c l o s u r e closure closure和 D F A e d g e DFAedge DFAedge算法,就能构造出DFA,DFA的状态 d 1 d_1 d1就是 c l o s u r e ( s 1 ) closure(s_1) closure(s1)。抽象而言,如果 d j = D F A e d g e ( d i , c ) d_j=DFAedge(d_i,c) dj=DFAedge(di,c)则存在一条从 d i d_i di 到 d j d_j dj 的标记为 c c c 的边。令 Σ \Sigma Σ 是字母表:
- s t a t e s [ 0 ] ← { } ; s t a t e s [ 1 ] ← c l o s u r e ( { s 1 } ) p ← 1 ; j ← 0 w h i l e j ≤ p f o r e a c h c ∈ Σ e ← D F A e d g e ( s t a t e s [ j ] , c ) i f e = s t a t e s [ i ] f o r s o m e i ≤ p t h e n t r a n s [ j , c ] ← i e l s e p ← p + 1 s t a t e s [ p ] ← e t r a n s [ j , c ] ← p j ← j + 1 states[0] \leftarrow \lbrace \rbrace; \qquad states[1] \leftarrow closure(\lbrace s_1 \rbrace) \\ p\leftarrow 1; \qquad j \leftarrow 0 \\ while \ j \leq p \\ \ \ \ foreach \ c \in \Sigma \\ \qquad e \leftarrow DFAedge(states[j],c) \\ \qquad if \ e =states[i] \ for \ some \ i \leq p \\ \qquad \quad \ then \ trans[j,c] \leftarrow i \\ \qquad \quad \ else \ p \leftarrow p+1 \\ \qquad \qquad \quad \, states[p] \leftarrow e \\ \qquad \qquad \quad \, trans[j,c] \leftarrow p \\ \; \; j \leftarrow j+1 states[0]←{};states[1]←closure({s1})p←1;j←0while j≤p foreach c∈Σe←DFAedge(states[j],c)if e=states[i] for some i≤p then trans[j,c]←i else p←p+1states[p]←etrans[j,c]←pj←j+1
解释一下: s t a t e [ ] state[] state[]代表了最终DFA的一个状态所对应的NFA状态集, s 1 s_1 s1为初始状态, c l o s u r e ( { s 1 } ) closure(\lbrace s_1 \rbrace) closure({s1})代表了初始状态 s 1 s_1 s1的闭包。上文中的代码实际上和龙书的代码一个意思,龙书的代码更加简单直白,所以这里可以跳过。等看完下面的龙书再回头来看
1.2 龙书概念
个人认为龙书的概念更加通俗易懂,但是由于没有数学公式的归纳,导致理论基础不扎实,有点慌。所以推荐两本书一起看。
首先,是概念:
- 子集构造法的基本思想是让构造得到的DFA的每个状态对应NFA的一个状态集合。DFA在读入 a 1 a 2 . . . a n a_1a_2...a_n a1a2...an之后到达的状态应该对应于相应的NFA从开始状态出发,沿着以 a 1 a 2 . . . a n a_1a_2...a_n a1a2...an为边的路径能达到的状态的集合。
解释一下:概念很直观哈,我就不解释了^_^
接着,是算法:
- 输入:一个NFA N
- 输出:一个接受同样语言的DFA D
- 方法:我们为算法 D 构造一个转换表 D t r a n Dtran Dtran。D的每个状态是一个NFA集合,构造 D t r a n Dtran Dtran,使得 D “并行地”模拟 N 在遇到一个给定输入串可能执行的所有动作。下面我们给出一些函数的定义:
| 操作 | 描述 |
|---|---|
| ϵ − c l o s u r e ( s ) \epsilon - closure(s) ϵ−closure(s) | 能够从NFA状态 s s s开始只通过 ϵ \epsilon ϵ转换到达的NFA状态集合 |
| ϵ − c l o s u r e ( T ) \epsilon - closure(T) ϵ−closure(T) | 能够从 T T T中某个NFA状态 s s s开始只通过 ϵ \epsilon ϵ转换到达的NFA状态集合,即 ⋃ s ∈ T ϵ − c l o s u r e ( s ) \bigcup_{s \in T} \epsilon -closure(s) ⋃s∈Tϵ−closure(s) |
| m o v e ( T , a ) move(T,a) move(T,a) | 能够从 T T T 中某个状态 s s s 出发通过标号为 a a a 的转换到达的NFA状态的集合 |
- 在读入第一个符号之前,N可以位于集合 ϵ − c l o s u r e ( s 0 ) \epsilon-closure(s_0) ϵ−closure(s0)中的任何状态上 ,其中, s 0 s_0 s0是 N 的开始状态。
- 下面进行回归纳:假定N在读入输入串 x x x之后可以位于集合T的任意状态上。如果下一个输入符号是 a a a,那么N可以立即移动到集合 m o v e ( T , a ) move(T,a) move(T,a)中的任何状态。然而,N 可以读入 a a a之后再执行几个 ϵ \epsilon ϵ转换,因此 N 在读入 x a xa xa之后可以位于 ϵ − c l o s u r e ( m o v e ( T , a ) ) \epsilon-closure(move(T,a)) ϵ−closure(move(T,a))中的任意状态上。接着我们可以构造出转换函数 D t r a n Dtran Dtran:
- 一开始, ϵ − c l u s u r e ( s 0 ) \epsilon-clusure(s_0) ϵ−clusure(s0)是 D s t a t e s Dstates Dstates的唯一状态,且它未标记(请注意,“标记”是非常重要的概念);
- w h i l e ( 在 D s t a t e s 中 有 一 个 未 标 记 的 状 态 T ) { 给 T 加 上 标 记 ; f o r ( 每 个 输 入 符 号 a ) { U = ϵ − c l u s u r e ( m o v e ( T , a ) ) i f ( U 不 在 D s t a t e s 中 ) 将 U 加 入 D s t a t e s 中 , 且 不 加 标 记 ; D t r a n [ T , a ] = U } } while(在Dstates中有一个未标记的状态T) \lbrace \\ \quad \quad \ 给T加上标记; \\ \quad \quad \ for(每个输入符号a) \lbrace \\ \qquad \qquad \quad U=\epsilon-clusure\left(move(T,a) \right) \\ \qquad \qquad \quad if(U不在Dstates中) \\ \qquad \qquad \qquad \qquad \, 将U加入Dstates中,且不加标记; \\ \qquad \qquad \quad Dtran[T,a]=U \\ \quad \quad \ \rbrace \\ \rbrace while(在Dstates中有一个未标记的状态T){ 给T加上标记; for(每个输入符号a){U=ϵ−clusure(move(T,a))if(U不在Dstates中)将U加入Dstates中,且不加标记;Dtran[T,a]=U }}
解释一下:这部分代码和虎书上的代码意思相近,这个更好理解。算法里的 D t r a n [ T , a ] = ϵ − c l u s u r e ( m o v e ( T , a ) ) Dtran[T,a]=\epsilon-clusure\left(move(T,a) \right) Dtran[T,a]=ϵ−clusure(move(T,a))每个 D t r a n [ T , a ] Dtran[T,a] Dtran[T,a]都可能是DFA的一个状态。
2 举个例子解释
- 题目:给定一个正则表达式 ( a ∣ b ) ∗ a b b (a|b)^*abb (a∣b)∗abb的NFA,我们使用子集构造法构造DFA。
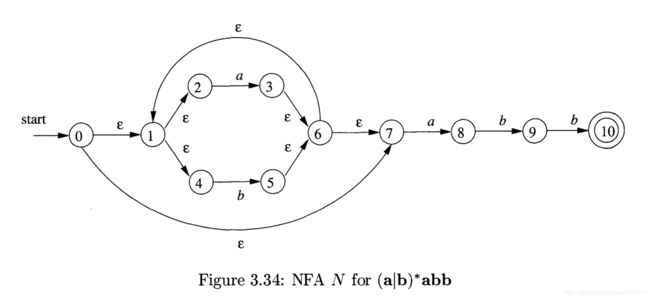
- 解法:首先,我们分析得出,NFA的初始为状态0。因而初始状态集 A = ϵ − c l o s u r e ( 0 ) = { 0 , 1 , 2 , 4 , 7 } A=\epsilon-closure(0)=\lbrace0,1,2,4,7 \rbrace A=ϵ−closure(0)={0,1,2,4,7}。
- A A A被加上标记,对于输入符号 a , b a,b a,b,分别求出:
a : B = ϵ − c l o s u r e ( m o v e ( A , a ) ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } b : C = ϵ − c l o s u r e ( m o v e ( A , b ) ) = { 1 , 2 , 4 , 5 , 6 , 7 } a:B=\epsilon-closure(move(A,a))=\lbrace1,2,3,4,6,7,8 \rbrace \\b:C=\epsilon-closure(move(A,b))=\lbrace1,2,4,5,6,7 \rbrace a:B=ϵ−closure(move(A,a))={1,2,3,4,6,7,8}b:C=ϵ−closure(move(A,b))={1,2,4,5,6,7} - B , C B,C B,C都没有被标记,因而将 B , C B,C B,C依次加上标记,对于输入符号 a , b a,b a,b,分别求出:
a : B = ϵ − c l o s u r e ( m o v e ( B , a ) ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } b : D = ϵ − c l o s u r e ( m o v e ( B , b ) ) = { 1 , 2 , 4 , 5 , 6 , 7 , 9 } a:B=\epsilon-closure(move(B,a))=\lbrace1,2,3,4,6,7,8 \rbrace \\b:D=\epsilon-closure(move(B,b))=\lbrace1,2,4,5,6,7,9 \rbrace a:B=ϵ−closure(move(B,a))={1,2,3,4,6,7,8}b:D=ϵ−closure(move(B,b))={1,2,4,5,6,7,9}
a : B = ϵ − c l o s u r e ( m o v e ( C , a ) ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } b : C = ϵ − c l o s u r e ( m o v e ( C , b ) ) = { 1 , 2 , 4 , 5 , 6 , 7 } a:B=\epsilon-closure(move(C,a))=\lbrace1,2,3,4,6,7,8 \rbrace \\b:C=\epsilon-closure(move(C,b))=\lbrace1,2,4,5,6,7 \rbrace a:B=ϵ−closure(move(C,a))={1,2,3,4,6,7,8}b:C=ϵ−closure(move(C,b))={1,2,4,5,6,7} - 现在只剩 D D D没有加标记,因而给 D D D加上标记,对于输入符号 a , b a,b a,b,分别求出:
a : B = ϵ − c l o s u r e ( m o v e ( D , a ) ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } b : E = ϵ − c l o s u r e ( m o v e ( D , b ) ) = { 1 , 2 , 4 , 5 , 6 , 7 , 10 } a:B=\epsilon-closure(move(D,a))=\lbrace1,2,3,4,6,7,8 \rbrace \\b:E=\epsilon-closure(move(D,b))=\lbrace1,2,4,5,6,7,10 \rbrace a:B=ϵ−closure(move(D,a))={1,2,3,4,6,7,8}b:E=ϵ−closure(move(D,b))={1,2,4,5,6,7,10} - 还剩一个 E E E没有标记,因而给 E E E加上标记,对于输入符号 a , b a,b a,b,分别求出:
a : B = ϵ − c l o s u r e ( m o v e ( E , a ) ) = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } b : C = ϵ − c l o s u r e ( m o v e ( E , b ) ) = { 1 , 2 , 4 , 5 , 6 , 7 } a:B=\epsilon-closure(move(E,a))=\lbrace1,2,3,4,6,7,8 \rbrace \\b:C=\epsilon-closure(move(E,b))=\lbrace1,2,4,5,6,7 \rbrace a:B=ϵ−closure(move(E,a))={1,2,3,4,6,7,8}b:C=ϵ−closure(move(E,b))={1,2,4,5,6,7} - 所有构造出来的集合都已经被标记,构造完成! A , B , C , D , E A,B,C,D,E A,B,C,D,E为五个不同状态:
A = { 0 , 1 , 2 , 4 , 7 } B = { 1 , 2 , 3 , 4 , 6 , 7 , 8 } C = { 1 , 2 , 4 , 5 , 6 , 7 } D = { 1 , 2 , 4 , 5 , 6 , 7 , 9 } E = { 1 , 2 , 4 , 5 , 6 , 7 , 10 } A=\lbrace0,1,2,4,7 \rbrace \\ B=\lbrace1,2,3,4,6,7,8 \rbrace \\ C=\lbrace1,2,4,5,6,7 \rbrace \\ D=\lbrace1,2,4,5,6,7,9 \rbrace \\ E=\lbrace1,2,4,5,6,7,10 \rbrace A={0,1,2,4,7}B={1,2,3,4,6,7,8}C={1,2,4,5,6,7}D={1,2,4,5,6,7,9}E={1,2,4,5,6,7,10} - 接着就是根据状态来画图了,最好先画好状态表:

- A A A被加上标记,对于输入符号 a , b a,b a,b,分别求出:
3 如何最小化DFA的状态数量
很简单,如果开始于 s 1 s_1 s1的机器接收字符串 σ \sigma σ,始于 s 2 s_2 s2的和始于与 s 1 s_1 s1接收的串相同,并到达相同状态,且两个状态集同为终态或者非终态,那么 s 1 , s 2 s_1,s_2 s1,s2是等价的。我们可以把指向 s 2 s_2 s2的连线全部指向 s 1 s_1 s1,并删除 s 2 s_2 s2,反之亦然。
- 举个书上的例子:
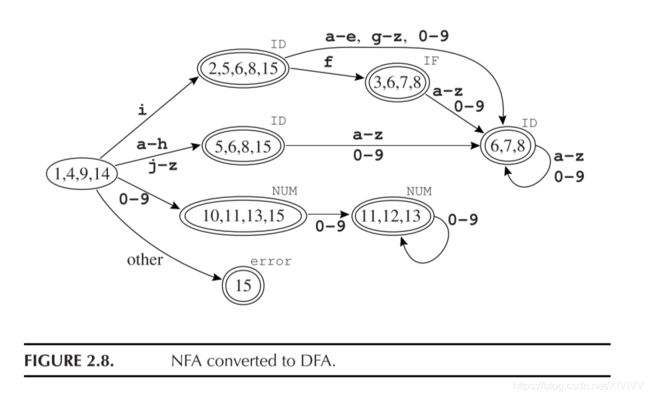
- 图中的 { 5 , 6 , 8 , 15 } , { 6 , 7 , 8 } \lbrace 5,6,8,15 \rbrace,\lbrace 6,7,8 \rbrace {5,6,8,15},{6,7,8}是等价的,还有 { 10 , 11 , 13 , 15 } , { 11 , 12 , 13 } \lbrace 10,11,13,15 \rbrace,\lbrace 11,12,13 \rbrace {10,11,13,15},{11,12,13}也是等价的。
Tips:在判断是否等价前,我们要先判断是否为死状态哦(1.不能到达终态 2.从开始没有路径指向这个状态)。
4 总结
NFA转DFA知识总结就到这里,有什么问题请留言,有错误请批评指正,非常感谢您的阅读。
