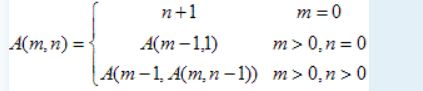DP练习之——HDU
DP练习之——HDU
前言：虽然做了将近50道题，但是感觉dp这方面还是不怎么样，状压dp，树形dp，插头dp这种比较难的dp问题都跳过了。
总的来说：也还是有所收获的，至少思维有所提升，未来的路还很长，加油！
day 1：
一、HDU 1025：Constructing Roads In JGShining’s Kingdom（题目链接）
题意：
开始看了好久的题意，毫无思路…其实就是求最长上升子序列
题解：
开始直接用的普通的O(n^2)的算法，结果TLE…
于是便利用了贪心的策略，通过二分查找计算最长上升子序列长度
具体思想：
假设要寻找最长上升子序列的序列是a[n]，然后寻找到的递增子序列放入到数组b中。
（1）当遍历到数组a的第一个元素的时候，就将这个元素放入到b数组中，以后遍历到的元素都和已经放入到b数组中的元素进行比较；
（2）如果比b数组中的每个元素都大，则将该元素插入到b数组的最后一个元素，并且b数组的长度要加1；
（3）如果比b数组中最后一个元素小，就要运用二分法进行查找，查找出第一个比该元素大的最小的元素，然后将其替换。
在这个过程中，只重复执行这两步就可以了，最后b数组的长度就是最长的上升子序列长度。例如：如该数列为：
5 9 4 1 3 7 6 7
那么：
5 //加入
5 9 //加入
4 9 //用4代替了5
1 9 //用1代替4
1 3 //用3代替9
1 3 7 //加入
1 3 6 //用6代替7
1 3 6 7 //加入
最后b中元素的个数就是最长递增子序列的大小，即4。
要注意的是最后数组里的元素并不就一定是所求的序列，
例如如果输入 2 5 1
那么最后得到的数组应该是 1 5
而实际上要求的序列是 2 5
（即：只能用来计算最长上升子序列的长度，不能用来构造最长上升子序列）
#include二、HDU 1058：Humble Numbers（题目链接）
题意：
给定一个数n，要你求第n个丑数的值（丑数：即素因子只能为2，3，5，7）
题解：
开始还没想到什么策略，其实只要从2，3，5，7的倍数入手即可。
如果一个数是Humble Numbers，那么它的2倍、3倍、5倍、7倍也都是Humble Numbers
于是状态转移方程为：
dp[n]=min(dp[i]*2,dp[j]*3,dp[k]*5,dp[l]*7)
i,j,k,l在被选择后相互移动
（有个英语知识点，居然让我wa了好几次…）
#include三、HDU 1059：Dividing（题目链接）
题意：
每组给出六个数，表示每个值的个数，其中相应的位置表示数的值，同样也表示你相应的代价
题解：
其实就是多重背包的模板题，看网上的题解要用二进制优化，但是我没用二进制优化也过了…
开始真的没想到这是多重背包，题目还是做少了
#include刚好10点，hdu关了…一天才做3道题，还是太懒散了
------------------------------------------------------我是分割线-----------------------------------------------------------------
day 2：
又是给社会做贡献的一天（hhh） 希望疫情早日得以解决，武汉加油，中国加油！！，今天边看题解，边写写画画，终于做了10道题，但是10点hdu关了，只好明天写小结了…
一、HDU 1069：Monkey and Banana（题目链接）
题意：
多组数据。每组数据给定一个n，表示有多少个长方体，其中每个长方体给出对应的长宽高，求最多能叠多高。
要求：上面的长方体的底面长宽均要大于下面的长方体的底面长宽
题解：
其实就是最长递增子序列LIS的长方体模型
由于给定长宽高不唯一，即：可以根据三个数值构造6个长方体，预先进行排序即可
#include二、HDU 1074：Doing Homework（题目链接）
只知道是状压DP，但是状压DP太难了。。。。
不会做啊
先放在这吧，等做完基础的了，再来看
三、HDU 1078：FatMouse and Cheese（题目链接）
题意：
类似于走迷宫。
胖老鼠走迷宫，其中每次最多走k步，迷宫中每个点都有对应的价值，求最多可以获得多少价值，要求：胖老鼠每次停下的地方的价值要大于原先停下来的价值
多组数据，每组数据给出迷宫的大小n（其中长宽相同），k。以及每个位置的价值
题解：
这种类似于迷宫问题，直接用记忆化搜索即可，需要注意的是，对于k这个条件要处理一下
#include四、HDU 1080：Human Gene Functions（题目链接）
题意：
可以理解为DNA匹配。
提前给出碱基相互对应的价值，然后每组数据给出两个字符串，判断最大的匹配值。
题解：
就是洛谷的P1140的改编题
刚好前段时间有做到，
#include五、HDU 1081：To The Max（题目链接）
题意：
n*n矩阵中，求最大子矩阵
题解：
直接套模板，需要注意的是long long
#include六、HDU 1087：Super Jumping! Jumping! Jumping!（题目链接）
题意：
多组数据，每组数据给出n，表示数组的长度，就是求最长上子序列LIS
题解：
这里不是求最长上升子序列长度，而是求和，只要稍微转换下即可
#include七、HDU 1114：Piggy-Bank（题目链接）
题意：
有一个储钱罐，给出储钱罐自身的重量，和装了钱的重量
然后有n种硬币，每种硬币有对应的价值和重量
求：储钱罐最少有多少钱
题解：
发现就是完全背包的裸题，需要注意的是：一般是求的最大值，这里求最小值，于是只需要对dp[]数组预处理为无穷大即可，然后dp[0]=0;
代码是利用的滚动数组
#include八、HDU 1121：Complete the Sequence（题目链接）
这题只能说比较难，为什么还说难度是1。可能是我太菜了吧，看了题解发现是差分，也就是牛顿插值法，虽然学过，但是不会编程啊。。。
看的大佬的代码：
#include九、HDU 1158：Employment Planning（题目链接）
为什么这也是难度1。。。
看了网上的题解后，自己写，然后一直RE。。。。
现在都还迷迷糊糊的
#include 十、HDU 1159：Common Subsequence（题目链接）
这题相比于上题有太简单了，就是求最长公共子序列的长度
也就没什么要多说的了，非常经典的模板题
#include做了这么多，发现简单的一维、二维的DP问题目前还是比较熟悉了
至于树形DP、状压DP等刷完简单的了，再好好恶补一下吧
day3：
今天有点懒散。。。
一、HDU 1160：FatMouse’s Speed（题目链接）
题意：
n对数，每对数有重量和速度组成，要求：在保证重量递增，速度递减的条件下；求最多能有多少对组成一序列
题解：
其实就是先排序后，求最长上升序列。需要注意的是：需要打印路径，于是结构体中要保存位置，同时还是用pre[]存储路径，直接用递归即可打印路径
#include二、HDU 1165：Eddy’s research II（题目链接）
题意：
给定n，m求A(m,n)
题解：
找规律，硬是用手算了好久，直接见代码，感觉如果比赛遇到这种题，还是有点逼心态的
#include三、HDU 1176：免费馅饼（题目链接）
题意：
开始站在位置为5的位置，每次能够接到他左右一个位置和他现在的位置的馅饼，题目会给出一段时间类，具体某个位置某个时间会掉馅饼，求最多可以获得多少个馅饼
题意：
其实还是比较容易想到状态转移方程的,但是由于正向dp不好处理，于是采用反向dp
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1],dp[i+1][j-1])+a[i][j];
（其中i表示时间，j表示位置）
又由于位置0不好处理，于是直接每个位置+1
最后只需要输出dp[0][6]即可
具体见代码：
#include四、HDU 1203：I NEED A OFFER!（题目链接）
题意：
n元钱，m个学校可以选择。每个学校都有对应的费用和能被录取上的概率，
求至少得到一个offer的最大概率
题解：
乍一眼看发现就是一个0-1背包。但是需要注意的是：题目求至少得到一个offer的最大概率p1，如果直接dp，结果其实是错的
于是不如逆向思考，先转化为一个offer都没有得到的最小概率p2，然后
p1=1-p2
#include五、HDU 1208：Pascal’s Travels（题目链接）
题意：
一个n*n的迷宫，每个位置都有对应的值，表示接下来走几步。题目要求从左上角走到右下角，只能向右和向下走
题解：
同样是迷宫类似问题，dp和记忆化搜索都可以，但是开始出现了点问题，看了看网上的博客才ac
记忆化搜索和dp都写了一下
dp数组版本：
注意dp[1][1]=1;不然没结果
#include记忆化搜索版本：
#include六、HDU 1224：Free DIY Tour（题目链接）
题意：
给出一个有向图，n个顶点，每个顶点有对应的价值，m条边构成有向图
要求从1开始最终回到1，问最多可以获得多少价值，同时打印路径
题解：
开始觉得是不是对最短路加以修改就行，但是没有弄出来，最终还是看的网上的博客，才发现原来可以这么弄，害，还是要加油
#includeday4：
下午和晚上有点事，就上午做了两道题。。。。
一、HDU 1227：Fast Food
题意：
n个餐馆，k个仓库。给定n个餐馆的位置，其中仓库可以位于任意k个餐馆的位置，求餐馆到达最近仓库的距离和
题解：
说实话，没怎么搞懂。。。。。
ps:在i到j取一点使它到区间每一点的距离之和最小,这一点为(i+j)/2用图形即可证明;
Dp[i][j]=max{Dp[i-1][k]+cost[k+1][j] 其中,(i-1)<=k 题意： 题解： 题意： 题解： 题意： 题解： 于是只给出dp数组方式代码（直接预处理即可） 题意： 题意： 题意： 题解： 直接按照优先选择最大的价值经过，于是代码就出来了 题意： 题解： 放一个大佬博客在这，等到时候强攻状压dp的时候再好好理解 https://blog.csdn.net/hopeztm/article/details/7841917 虽然做了好几道题，但是都不是自己开始就想到的，dp好难啊 题意： 题解： 当i>j*2时,dp[i][j] = min(dp[i-1][j],dp[i-2][j-1]+(w[i]-w[i-1])^2) 题意： 题解： 同时加一个maxpos==n时，跳出循环 需要注意的是：这里是个环形的。。。。，所以数组开为两倍即可 题意： 题解： 题意： 题解： 然后用bfs处理最短路，记忆化搜索获得最短路径数 自己还是很菜啊！！！ 题意： 题解： dp[直线的总数][交点的个数] = 状态(本状态存在为1，不存在为0) 一道之前校内选拔赛老师选的一道题，结果还是没有做出来。。。。 题意： 题解： 其实dp状态应该为 最后只需要判断dp[len1][len2]是不是等于1 dp[i][j][k]=dp[i-1][[j][k]+dp[i][j-1][k]+dp[i][j][k-1] 然后一顿操作猛如虎，结果wa 原来是会暴long long，也就是大整数，于是立马用Java的BigInteger 题意： 题解： 题意： 题解： 题意： 题解： 但是由于字符串长度比较大，必须使用滚动数组，具体见代码 题意： 题解： 题意： 求依次经过n件事件后，最终的收益值 题解： 树形dp，先放在这 状压dp 插头dp 题意： 求在m时间内，能得到的最大价值 题解： 总觉得这题是背包问题，但是就是 没有什么思路.。。 题意： 题意： dp[n]=dp[n-1]+dp[n-2]+…+dp[n-m];#include 二、HDU 1243：反恐训练营
给定n表示子弹的类型和恐怖分子类型（其中：子弹类型必须与恐怖分子类型相同，才能获得恐怖分子的分数），然后给出恐怖分子序列，以及：每种类型的对应得分。然后给出子弹的类型，求最多能获得多少得分
居然开始没想到，其实就是LCS（最长公共子序列）模型啊
只是每个字符都有价值而已#includeday 5：
一、HDU 1300：Pearls
n种珠宝，每种珠宝有对应的数量和价格，按照题目的规则求最终买入所有珠宝的总费用最小
Dp[i]=min{Dp[j]+V}, 0<=j#include二、HDU 1331：Function Run Fun
求w(a,b,c)
然后规则是：
很明显直接递归肯定会tle
记忆化搜索或者直接用dp数组存都可，但是不知道为什么我的记忆化搜索tle了。。。。#include三、HDU 1337：The Drunk Jailer
不知道为什么hdu把它放到dp题
直接求n的平方根即为答案#include四、HDU 1355：The Peanuts
感觉像是做过的题目，给出n*m的矩阵，矩阵每个点有对应价值，然后矩阵上方有一道路，每次必须优先选择价值最多的经过，而且或者该点的价值需要一单位时间，走一单位距离也需要一单位时间，问最终在给定允许的时间内，能获得的最多价值
感觉还是不是dp啊，应该是贪心或者是模拟啊#include五、HDU 1400：Mondriaan’s Dream
给定一大矩阵，求通过若干1*2的子矩阵能有多少种组合方式
据说是非常经典的状压dp题，但是我不知道做（呜呜呜… ）day 6：
一、HDU 1421：搬教室
n件物品，但是只需要搬2*k件过去
题目给出每个物品的重量，每次能搬两件，受到的疲劳度为两者的差的平方
求最少能受到的疲劳度
状态dp[i][j]为前i件物品选j对的最优解
当i=j*2时,只有一种选择即 dp[i-2][j-1]+(w[i]-w[i-1])^2#include二、HDU 1422：重温世界杯
n个城市，每个城市都对应有着花费和生活费，而且最初也有一定的生活费，问最多能逛多少个城市
1.如果剩下的钱(res)加上当前城市的生活费(w[i])>=当前城市的消费(l[i])
dp[i]=dp[i-1]+1;
res=res+w[i]-l[i];
2.否则剩下的钱置为0#include三、HDU 1423：Greatest Common Increasing Subsequence
求最长公共递增子序列
这里其实降低了难度，只要求长度，没有要求构造
到网上看到了一个非常巧的代码，主要是代码短小精悍#include四、HDU 1428：漫步校园
n*n的地图，要求从走上角走到右下角。每个位置都有对应的代价，求有多少条不同的最短路径。
发现这题用简单的dp不能解决，但是自己还是无能为力，只好看了网上的题解，最短路+dp#include五、HDU 1466：计算直线的交点数
n条直线，问有多少条相交方案
感觉这个dp状态转移方程还是比较难想。。。#include六、HDU 1494：跑跑卡丁车
#include七、HDU 1501：Zipper
给定两个短字符串，和一个长字符串
判断长字符串是不是有这两个短字符串组成
开始还天真的觉得只要判断两个短字符串分别与长字符串求最长公共子序列即可，如果两者的结果之和等于长字符串的长度则正确yes，否则noif(dp[i][j-1]&&s2[j]==str[i+j]){
dp[i][j]=1;
}
if(dp[i-1][j]&&s1[i]==str[i+j]){
dp[i][j]=1;
}
#include八、HDU 1502：Regular Words
（i>=j&&j>=k）import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.*;
public class Main {
public static void main(String args[]) {
BigInteger dp[][][]=new BigInteger[100][100][100];
/**
* 初始化dp数组
*/
for(int i=0;i<=60;i++) {
for(int j=0;j<=60;j++) {
for(int k=0;k<=60;k++) {
dp[i][j][k]=BigInteger.ZERO;
}
}
}
dp[0][0][0]=BigInteger.ONE;
for(int i=0;i<=60;i++) {
for(int j=0;j<=60;j++) {
for(int k=0;k<=60;k++) {
int x=i-1;
int y=j-1;
int z=k-1;
if(x>=0&&j>=0&&k>=0&&x>=j&&x>=k&&j>=k) {
dp[i][j][k]=dp[i][j][k].add(dp[i-1][j][k]);
}
if(i>=0&&y>=0&&k>=0&&i>=y&&x>=k&&y>=k) {
dp[i][j][k]=dp[i][j][k].add(dp[i][j-1][k]);
}
if(i>=0&&j>=0&&z>=0&&i>=j&&x>=z&&y>=z) {
dp[i][j][k]=dp[i][j][k].add(dp[i][j][k-1]);
}
}
}
}
Scanner scan=new Scanner(System.in);
while(scan.hasNext()) {
int n=scan.nextInt();
System.out.println(dp[n][n][n]);
System.out.println();
}
}
}
day 7：
一、HDU 1506：Largest Rectangle in a Histogram
n个矩阵，求高相同的情况最大矩形面积
说实话不是很懂。。。。#include二、HDU 1505：City Game
1506的加强版，这次是求二维的面积#include三、HDU 1513：Palindrome
给定一字符串，并且还告诉你它的长度，求加几个字符能是其成为回文字符串
开始真的一脸懵逼，但是构造一个 字符串由给定字符串的翻转得来
求：最长公共子序列长度即为答案#includeday 8：
一、HDU 1559：最大子矩阵
mn的矩形，从中选择xy的子矩阵，问最大子矩阵为多少
很明显的dp问题，但是感觉处理起来还是有点技巧的，具体见代码#include二、HDU 1574：RP问题
n个事件，每个事件对应有RP变化值a、RP门槛值b和获益值c
当RP变化值a为正，获益值c必定为负，只有你当前的RP值小于等于RP门槛值b的时候，此事件才有可能发生，当此事件发生时，你的RP值将增加|a|，获益值将减少|c|。反之，当RP变化值a为负，获益值c必定为正，只有你当前的RP值大于等于RP门槛值b的时候，此事件才有可能发生，当此事件发生时，你的RP值将减少|a|，获益值将增加|c|。
0-1背包的变形，但是还是有点难想#include三、HDU 1561：The more, The Better
四、HDU 1565：方格取数(1)
五、HDU 1693：Eat the Trees
六、HDU 1712：ACboy needs your help
有n门课程，m个单位时间
给出一矩阵，a[i][j]表示：i门课程花j时间得到的价值
于是又一次看了看背包九讲
这不就是典型的分组背包吗#include七、HDU 1723：Distribute Message
n个人排成一行，现在要求将一物品从第一个人传到第n个人
其中每个人最多可以跳多m个位置
问有多少种方案
（题意自己稍微修改了下文字，哈哈哈，觉得这样好理解些）
比较简单的dp问题#include