Apollo进阶课程㉓丨Apollo规划技术详解——Motion Planning with Environment
原创： 阿波君 Apollo开发者社区 6月26日
当行为层决定要在当前环境中执行的驾驶行为时，其可以是例如巡航-车道，改变车道或右转，所选择的行为必须被转换成路径或轨迹，可由低级反馈控制器跟踪。所产生的路径或轨迹必须满足车辆动力学约束的，对乘客来说是舒适的，并且避免与车载传感器检测到的障碍物的碰撞。寻找这样的路径或轨迹的任务是运动规划系统的责任。
由于规划是感知和控制之间的纽带，当前的新规划算法开发多考虑感知的不确定性以及控制的约束。在动态环境数据采集过程中，路径规划的最新发展目标是正确处理数据采集过程中的不确定性。这在实时的情况下会有更好的环境感知效果，并指导规划过程。通过考虑感知阶段的不确定性来提高防止危险情况的能力。从控制的角度来看，需考虑多目标，包括车辆的运动学约束和乘客的舒适性等。
上周阿波君为大家详细介绍了「进阶课程㉒Apollo规划技术详解——Motion Planning with Autonomous Driving」。
主要介绍了运动规划的一些基本方法，重点从robotics的角度阐释。包括有RRT（基于快速扩展随机树算法）、Lattice网络方法、Spira方法、Polynomial方法、Functional Optimization方法等。
本周阿波君将与大家分享Apollo规划技术详解——Motion Planning with Environment。下面，我们一起进入进阶课程第23期。
目录
1.运动规划的环境变化
2.Vehicle Model的建立
3.曲线坐标系SL
4.SL坐标系到XY坐标系的投影
5.XY坐标系到SL坐标系的投影
1.运动规划的环境变化
运动规划根据环境的变化在算法和处理方法上有很大的不同，涉及到模型建立、平滑优化和坐标转换以及障碍物投影等。如下图所示。
运动规划的环境变化
2.Vehicle Model的建立
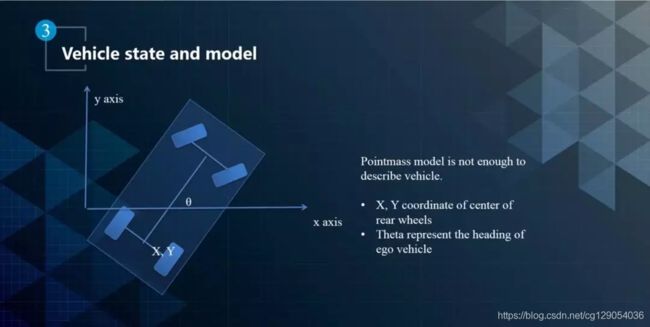
Vehicle Model的建立
对于汽车而言，质点模型是远远不够的，无人车是前轮转向的车，前后位置的变化是不一样的，那么怎么去描述这种不一样呢？首先从刚体角度考虑，二维平面里的刚体涉及到
和
，也就是以车后轴中心作为坐标原点时车身的朝向heading。因为无人车运动模型还多了一个转向的变量，多了一个自由度，刚体模型也不够。
可以将汽车运动模型简化为自行车模型，将四轮抽象成两个轮子，前轮中心和后轮中心的运动方向和自行车一样。车辆在垂直方向的运动被忽略掉，用一个二维平面上的运动物体来描述车辆的运动模型。自行车运动的时候具有以下特点，旋转车头的时候，前轮和后轮都围绕一个中心点转动，并且后轮的转向半径
与方向盘转动角度
满足以下关系，其中L为前轮中心和后轮中心的距离:
运动规划与车辆模型
实际的自行车运动模型
在实际的自行车运动模型中，后轴中心是沿着如上图所示的一条平滑的轨迹运行，该轨迹对应的曲率
表示调整方向盘的度数，如果为正，表示向左转，反之则向右转。因此，自行车运动模型可以用
，
，，k还有速度
来表示。那么沿着这样的轨迹运动时，如何去估计障碍物的距离呢？解决这个问题，先了解一下曲线坐标系以及与世界坐标系之间的转换关系。
3.曲线坐标系SL
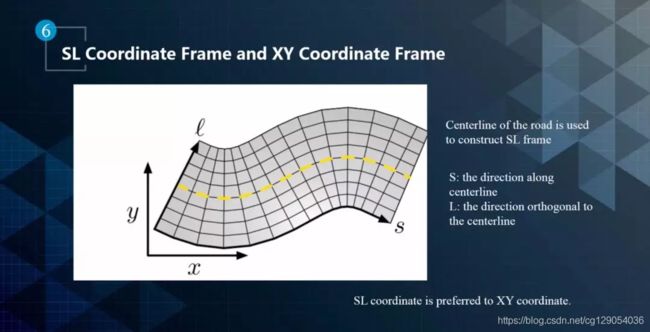
SL坐标系也叫做frenet frame，如下所示。它以道路中心线为参考，S表示道路中心线的方向，L表示与道路中心线垂直的方向。在结构化道路上行驶的时候，SL坐标系比XY坐标系更加贴合实际需求。那么SL坐标系如何转换到XY坐标系呢？
SL坐标系和XY坐标系
4.SL坐标系到XY坐标系的投影
之所以要投影到世界坐标系，是因为很多信息是全局的，例如红绿灯位置，参考的是XY世界坐标系。在给定SL坐标系时，每一个点的S坐标本身对应一个
坐标，根据该点的横向偏移距离，可以求出给定点在世界坐标系中的XY位置，如下图所示。其中theta是参考线的方向，也就是切线方向。如果XY与S方向平行的话，轨迹的曲率还满足图中所示的关系。
SL坐标系到XY坐标系的投影
5.XY坐标系到SL坐标系的投影
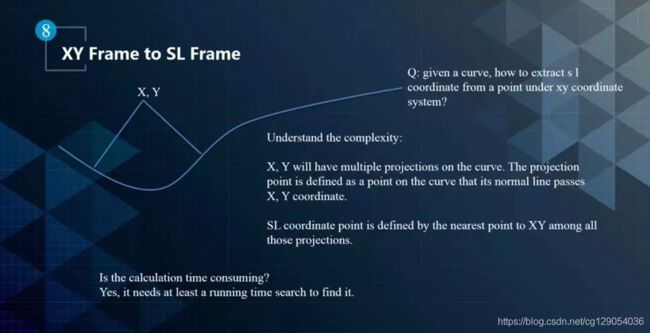
对于一个给定的曲线，如何将XY坐标系下的点转换到SL坐标系呢？因为SL坐标系并不是唯一的，XY会在曲线上产生很多投影，投影点是经过XY坐标，且垂直于曲线的线段与曲线的交点，如下图所示，XY就有两个投影点。通常情况下会增加一些限制，例如投影距离不能超曲率值。需要注意的是，掉头的时候还是需要特殊处理的。
XY坐标系到SL坐标系的投影