链接:https://ac.nowcoder.com/acm/contest/277/D
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
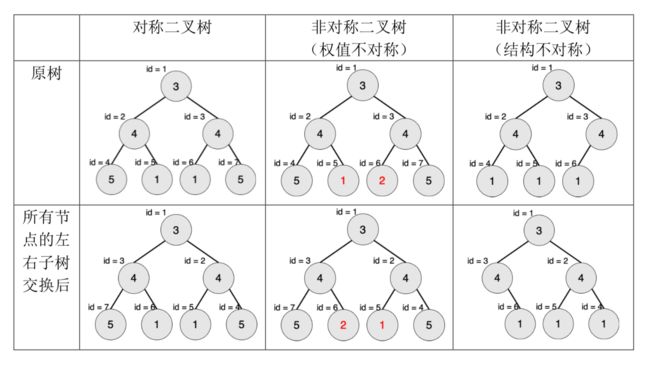
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
1. 二叉树;
2. 将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的 id 表示节点编号。
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 T为子树根的一棵“子树”指的是:节点T和它的全部后代节点构成的二叉树。
本题约定: 层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节
点的层次等于其父亲节点的层次加 1。 树的深度:树中节点的最大层次称为树的深度。
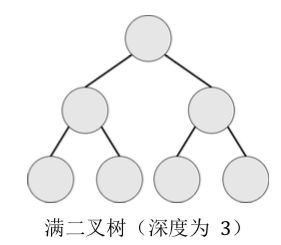
满二叉树:设二叉树的深度为 h,且二叉树有 2h − 1 个节点,这就是满二叉树。
完全二叉树:设二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大
个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。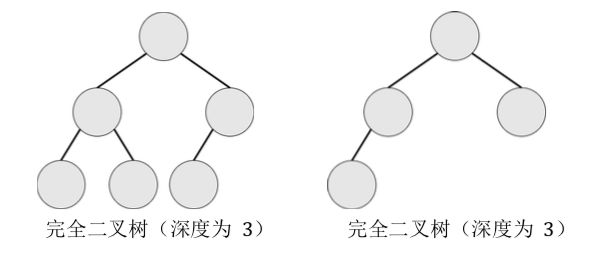
输入描述:
第一行一个正整数 ?,表示给定的树的节点的数目,规定节点编号 1~n,其中节点1 是树根。
第二行 ? 个正整数,用一个空格分隔,第 ? 个正整数 ?? 代表节点 ? 的权值。
接下来 ? 行,每行两个正整数 ? , ? ,分别表示节点 ? 的左右孩子的编号。如果不存在左 / 右孩子,则以 −1 表示。两个数之间用一个空格隔开。输出描述:
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
示例1
输入
复制
2
1 3
2 -1
-1 -1输出
复制
1说明
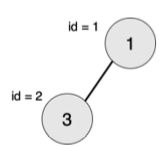
最大的对称二叉子树为以节点 2 为树根的子树,节点数为 1。
示例2
输入
复制
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8输出
复制
3说明
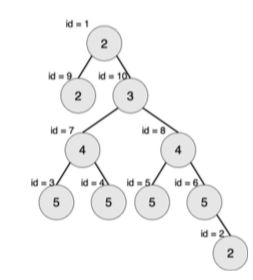
最大的对称二叉子树为以节点 7 为树根的子树,节点数为 3。
备注:
共 25 个测试点。 ?? ≤ 1000。
测试点 1~3,? ≤ 10,保证根结点的左子树的所有节点都没有右孩子,根结点的右 子树的所有节点都没有左孩子。
测试点 4~8,? ≤ 10。
测试点 9~12,? ≤ 105,保证输入是一棵“满二叉树”。
测试点 13~16,? ≤ 105,保证输入是一棵“完全二叉树”。
测试点 17~20,? ≤ 105,保证输入的树的点权均为 1。
测试点 21~25,? ≤ 106。
AC代码
#include
#include
using namespace std;
const int maxn=1e6+5;
struct node{
int data;
int lc;
int rc;
int siz;
}a[maxn];
int dfs(int root){
if(root==-1) return 0;
return a[root].siz=1+dfs(a[root].lc)+dfs(a[root].rc);
}
bool issame(int ra,int rb){
if(ra==-1&&rb==-1) return 1;
if(ra==-1&&rb!=-1) return 0;
if(ra!=-1&&rb==-1) return 0;
//if(a[ra].data==a[rb].data) return 1;
if(a[ra].data!=a[rb].data) return 0;
return issame(a[ra].lc,a[rb].rc)&&issame(a[ra].rc,a[rb].lc);
}
bool ok(int root){
return issame(a[root].lc,a[root].rc);
}
int main(){
ios_base::sync_with_stdio(false);
int n; cin>>n;
for(int i=1;i<=n;i++) cin>>a[i].data;
for(int i=1;i<=n;i++) cin>>a[i].lc>>a[i].rc;
dfs(1);
int ans=0;
for(int i=1;i<=n;i++){
if(ok(i))
ans=max(ans,a[i].siz);
}
cout<