Manacher's Algorithm ----马拉车算法（【USACO题库】1.3.3 Calf Flac）

题目描述

据说如果你给无限只母牛和无限台巨型便携式电脑(有非常大的键盘),那么母牛们会制造出世上最棒的回文。
你的工作就是去这些牛制造的奇观(最棒的回文)。
在寻找回文时不用理睬那些标点符号、空格(但应该保留下来以便做为答案输出),只用考虑字母’A’-‘Z’和’a’-‘z’。
要你寻找的最长的回文的文章是一个不超过20,000个字符的字符串。
我们将保证最长的回文不会超过2,000个字符(在除去标点符号、空格之前)。

PROGRAM NAME: calfflac

INPUT FORMAT
一个不超过20,000个字符的文件。

SAMPLE INPUT (file calfflac.in)
Confucius say: Madam, I’m Adam.

OUTPUT FORMAT
输出的第一行应该包括找到的最长的回文的长度。
下一个行或几行应该包括这个回文的原文(没有除去标点符号、空格),
把这个回文输出到一行或多行(如果回文中包括换行符)。
如果有多个回文长度都等于最大值,输出那个前出现的。

SAMPLE OUTPUT (file calfflac.out)
11
Madam, I’m Adam

中心搜索法

具体可以去看我一年前写的博客：
【USACO题库】1.3.3 Calf Flac
时间$O(N^2)$，如果数据坑的话过不去。

Manacher’s Algorithm

中心搜索的瓶颈在于，如果回文串互相覆盖，就会重复计算很多次。
比如s=“aaaaaaaaaa"或"abacabadabacaba”
（当然如果互不覆盖时间就是$O(|S|)$了）

但是如果像这样一种情况，很显然可以直接得出答案：

为了方便计算，我们在两两字符中间插入一个特殊字符（比如!@#$%^&*之类的）

这样可以避免分开处理奇偶性。

正题

设p[i]表示以第i个位置为中心的最长回文串半径。

那么问题来了，挖掘机
如何在线性时间内求出p数组？

比如说我现在求到这里：

那么之前到达边界最远的位置是第9位的c，范围如下

因为对应的位置半径为4，而半径为4时已经碰到了右边界，只能说明当前半径≥4。
所以对于半径>4的地方是未知的，要暴力去判断。
判断完以后，要更新最远位置。

相比之下，如果是这样的情况，半径为2，没有超过范围，就可以直接赋值。

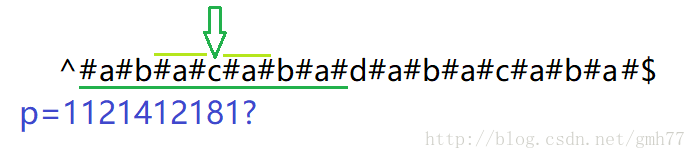
大概流程

如果当前位置加上半径大于等于边界，就从边界开始扩展，扩展完后更新边界，
否则直接取对称点的半径。

code

var
        p:array[0..40005] of longint;
        a:array[0..40000] of longint;
        i,j,k,l,r,len,ii,max,max2:longint;
        s,ss:ansistring;
        ch:char;
begin
        assign(Input,'fuck.in'); reset(Input);

        i:=0;
        a[1]:=0;
        a[2]:=0;
        a[0]:=2;
        s:='^@';
        repeat
                read(ch);
                inc(i);

                ss:=ss+ch;

                if (ch in['A'..'Z','a'..'z']) then
                begin
                        s:=s+upcase(ch)+'@';

                        inc(a[0]);
                        a[a[0]]:=i;
                        inc(a[0]);
                        a[a[0]]:=i;
                end;
        until eof;//初始化

        s:=s+'$';

        inc(a[0]);
        a[a[0]]:=i;

        len:=length(s);

        k:=1;
        l:=1;
        r:=1;
        p[0]:=1;
        p[1]:=1;
        max:=1;
        max2:=1;

        for i:=2 to len do
        begin
                j:=k-(i-k);

                if (j<=0) or ((p[j]+i-1)>=r) then//碰到或超出边界
                begin
                        if (i>=r) then
                        begin
                                l:=i;
                                r:=i;
                        end;

                        ii:=r-i;
                        while (((i-ii-1)>0) and ((i+ii)max) then
                        begin
                                max:=p[i];
                                max2:=i;
                        end;

                        k:=i;
                        l:=i-p[i]+1;
                        r:=i+p[i]-1;
                end
                else
                p[i]:=p[j];
        end;

        writeln(max-1);

        while (not (ss[a[max2+p[max2]]-1]in['A'..'Z','a'..'z'])) do
        dec(a[max2+p[max2]]);

        for i:=a[max2-p[max2]+2] to a[max2+p[max2]]-1 do
        write(ss[i]);
        writeln;
end.