近期总结2
莫队:https://www.cnblogs.com/WAMonster/p/10118934.html
使用条件:查询连续一段区间,且扩张或缩小区间两端的复杂度优秀.
做法:离线,把序列分块,把L,R按所在块的编号从小到大双关键字排序.每次移动查询.
优化:排序时l递增,在l的块为奇数时R递增,为偶数时R递减.
带修莫队:加入一个修改的时间戳,也作为关键字排序,然后分的块大小为n^(3/4)*t^(1/3)或者记不住的话就是n^(2/3).
树上莫队:给树弄一个欧拉序,就是每个点进来时记录在队,出去时也记录在队,共记录两次.然后查询x到y的路径.设每个点的编号x首次出现的位置first[x],最后出现的位置为last[x],令first[x]<=first[y](不满足则swap),如果lca(x,y)=x,则直接把[first[x],first[y]]的区间扯过来用,反之使用[last[x],first[y]]区间再在查询时加上公共祖先.
回滚莫队:有的扩张容易缩小困难(比如维护的时最大值).那我们就只让它扩张.具体来说就是先暴力处理在同一块的查询,然后按l所在的块逐块搞定. 每次将R向后推进,l则复原在块尾,然后向前推进.
分块:
区间众数:https://www.docin.com/p-679227660.html
结论:一段区间的众数,它的可能选项为它的一个子区间的区间众数,和除去这个子区间外的所有数(这些数可以包含子区间内的数.
若查询l,r在一块中则暴力,在不同块中,则众数由l的散块,r的散块,和中间的整块构成.
预处理任意两块间的众数,再预处理f[i][x]表示第1~i块中x出现的次数,g[k][i][x]表示在第k块中,到第i个,x出现次数(预处理时空复杂度O(n*根号n)).
根据结论,可得众数只可能由整块的众数,散块的所有数共2*根号n个构成,一个一个去计量它们在区间中出现的次数,去比较,其实预处理之后就是O(n*根号n)了.
如果还有修改操作,我们就要把块的个数变成L=n^(1/3),这样每次修改一个数,最多可能会影响L*L个块组之间的答案.
对每块之间,维护每个值的出现次数以及最大的出现次数.再将更改的那个值所在块的g修改一部分.
O((n+q)^(2/3))
分块题目http://hzwer.com/8053.html
大概思路:预处理,处理整块,处理散块. 有时数组可以用数据结构替代.有些操作如开方,整体赋值,很容易就会把大量数弄得相等,若一个块内数字相等可以判掉. 如果有插入的,一个块内内容太大,就拆成两半或重新分块.
异或高斯消元:
M[0][0]*x[0]^M[0][1]*x[1]^…^M[0][N-1]*x[N-1]=B[0]
M[1][0]*x[0]^M[1][1]*x[1]^…^M[1][N-1]*x[N-1]=B[1]
…
M[N-1][0]*x[0]^M[N-1][1]*x[1]^…^M[N-1][N-1]*x[N-1]=B[N-1]
其中每个系数都是0或1.
然后其实和普通高斯消元差不多,先找到一个第一列系数为1的行,扔到第一行,并靠它消去其它所有第一列系数也为1的行的那个1.其它类推.
线性基:https://blog.csdn.net/a_forever_dream/article/details/83654397
定义:对于一个序列,在它的线性基中选出一个或若干个数,异或起来,一定可以表示出这个序列中的所有数字.
性质:线性基中没有多余的数字,每一个数字都是有用的,也就是说对于线性基中每一个数字,它都不可以由其它数字表示.一个序列可能存在多个线性基,但每个线性基的元素个数都是相同且最少的.
构造方法:在序列中每次枚举一个x,判断它是否能够插入线性基中.具体来说定义f[i]表示二进制第i位为1且最高位为第i位的一个线性基中的元素.从高位到低位枚举位数,如果x在那一位上有值,且f[i]暂时没值,就把f[i]赋值成x,跳出.如果x在那一位上有值,且f[i]也已经有值,就要把x异或上f[i]然后继续.
这样构造出来的线性基并不能满足一个线性基元素上最高位的1是唯一的,因此还要消去一些位上的1.(这样处理后也是另一种形式的线性基)
求一个序列中元素异或起来的最大值:
因为线性基中的元素异或起来所能得到的值,和序列中元素异或起来所能得到的值,是一样的.所以直接看线性基.从高到低枚举,如果异或f[i]能变大就异或.
求最小值:直接找线性基中最小的那个元素吧.(因为它占据最小位,让它异或别人它一定更大
求第k小:对于每一个f[i]有值的位,在第i位上它的1都是唯一的,也就是说选它或不选它两种可能就会造成两种不同的异或结果.所以如果k的第i位为1时就选,反之就不选.第k大选的条件相反.
判断一个x是否可以由线性基中的元素构成,且由哪几个:
尝试把x插入线性基中,失败则是可以构成,而一路上异或的线性基元素就是构造方法,记录下来.
LCT:
https://www.cnblogs.com/flashhu/p/8324551.html
https://blog.csdn.net/blue_cuso4/article/details/78618811
开坑!
LCT是支持树的连边断边的一种数据结构.(只讲基础了扩展我真的学不会
有一棵原树,有一棵辅助树,原树上有些边是重边,有些是轻边.但它的重边和轻边并非固定的,而是可以变化的.
每一条重链,用splay按深度维护.每个splay呢,由它的根,向上连一条有向边,连的对象呢,是splay中那个深度最小的点的父亲.
这些有向(两个splay间的边)无向(每个splay内部的边)的边呢,就构成了一棵辅助树.
LCT有几个基本操作:
access(x):意思就是将原树中的点x到根节点的路径上,每一条都变成重边.注意此时将x的所有重儿子断掉,x是所属splay中最深的点(所以它没有右儿子了.
具体来说呢,分为几个步骤:
1.将x点(操作点),splay到当前splay的根,然后把它的右儿子单方面断掉,(如果这不是第一次操作,将接上上一次操作的点作为x的右儿子
2.将操作点切换为单向边所指的父亲,进入另一棵splay,然后返回操作1.
reverse(x):换根,将原树的x节点变成整棵树的根(势必会带来些深度的变化)
因为原树是虚树,在原树上变换其实是在辅助树上变换.
先access(x),这样整棵树的根与x就在同一个splay中了.接着将x转到splay的根(因为access断掉了x下方的重儿子,所以x在splay是没有右儿子的,相当于x在splay中深度最大).
现在深度最大的点,要把它当作深度最小的,原来深度最小的根,则变成深度最大的,这就相当于要将整个splay翻转过来,该棵splay中,左儿子变成右儿子,右儿子变成左二子(怎么有种礼崩乐坏的感觉. 而不在该棵splay中的点,他们的深度关系并不发生改变(深度可能是有改变,但彼此间深度大小关系不变),于是不用翻转.
froot(x):找到x所在原树的树根(主要是用来判断联通性的,froot(x)==froot(y)才联通)
先access(x)打通它和根的通道,接着将x点splay到splay的根,原树的根深度最小,一定在这棵splay的最左边,不断往左找(记得下传翻转标签.
link(x,y):将两个不连通的点联通,换言之,将它们所属的两棵树合并.
首先进行reverse操作,将一个点作为它所在树的根,然后将这个点的father单向接到另一个点上,连完了一条轻边.
当然如果题目不保证x,y之前不连通的话,还要判断froot(x)是否等于froot(y).
cut(x,y):将x,y之间的边断开.
先reverse(x)将x作为根,然后access(y)使x与y在同一棵splay中,然后将y旋转到splay的根,由于x,y本来有边相连,且x深度比y浅,所以这时x必然在它的左节点,把这条边彻底断掉吧.
如果题目没有保证x,y本来相连,那就要麻烦一些.
判断x,y相连有三个条件:
1.它们两在同一个原树中.
2.将x定为原树的根,access(y)后,splay(x),则y的父亲要是x.
3.此时y没有左儿子.
关于条件的解释:
1.不在同一棵树不可能相连啦,pass!
2.access(y)后,x与y在同一棵splay中,并且y下面的重儿子都被断掉了,也就是说y是深度最大的那个.y一定不会位于某个点的左侧,如果x,y不直接相连,那么它们的中序遍历x,y中必定有点夹着.
3.就算是x,y在辅助树上直接相连,在原树中它们也不一定直接相连.因为是中序遍历,如果y有左儿子,则中序遍历从x下来必定先到y的左儿子,这样x,y就不在原树直接相连了.
板题:https://www.luogu.com.cn/problem/P3690
Over!
欧拉函数:
定义φ(x)表示在[1,x]中与x互质的数的个数,其中φ(1)=1.
公式是:
其中pi为x的质因子,且pi都互不相同(重复的质数因子就只算一个
欧拉函数有几个性质:
1.积性函数.也就是说若m,n互质,则![]()
2.若x是质数,φ(x)=x-1.
3.若x是质数p的k次方(即x=p^k),则φ(x)=x-x/p=p^k-p^(k-1)=(p-1)*(p^(k-1)). (除了p的倍数,其余的[1,x]中的数都与x互质,而[1,x]中是p的倍数的有x/p个.)
4.当x是奇质数时,φ(2x)=φ(x)*φ(2)=φ(x)=x-1
于是如果我们要求单个的φ(x),我们可以把x分解质因数,x=p1^a1*p2^a2*p3^a3.....,根据积性函数的性质,φ(x)=φ(p1^a1)*φ(p2^a2)...,然后根据性质3,φ(p1^a1)=p1^a1-p1^(a1-1).其它类推.(其实也可以不用管这种zz做法,直接按定义来就行了.分数的话用x来除一定可以除尽.
如果我们要求出1~n中所有的φ(i),就要根据积性函数的性质.
令n=m*p,p为质数,则若m%p==0,φ(n)=φ(m)*p(这个把它按照定义化出来就可以证明),反之φ(n)=φ(m)*(p-1)(根据积性函数性质)
既然这样,我们可以从小到大找到每个数,随便找它的一个质因数,然后用上式.
欧拉函数在反演中有两条式子:
![]() 就是说n的所有约数的欧拉函数和等于n (其实把G(n)当作n,φ(d)当作F(d),这个形式就是莫比乌斯反演的形式.
就是说n的所有约数的欧拉函数和等于n (其实把G(n)当作n,φ(d)当作F(d),这个形式就是莫比乌斯反演的形式.
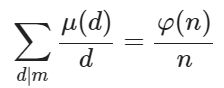 (那个m应该是n才对) 左边通分,两边同去n,然后用上面的莫比乌斯反演形式来反演
(那个m应该是n才对) 左边通分,两边同去n,然后用上面的莫比乌斯反演形式来反演
反演:
(最讨厌这些数学内容了
这里就是说s和x是两个集合,其中x要保证为s的子集,G(s)=所有合法的x的F(x)之和.
然后我们想想,G(x)=F(x)+F(x所有其它的子集) ,F(x)=G(x)-G(所有大小比x少1的子集)+G(所有大小比x少2的子集),用到容斥.
本质也是容斥.注意是要不同的质数构成才算,相同的就为0了
几个高级(沙雕)公式
 组合数可以证明.d作为m的一个约数,它可能包含奇数个质因子,也可能有偶数个质因子,还可能有重复而不算.
组合数可以证明.d作为m的一个约数,它可能包含奇数个质因子,也可能有偶数个质因子,还可能有重复而不算.
 把F(n)当作1,把G(d)当作
把F(n)当作1,把G(d)当作![]() ,发现形式一毛一样.然后反演回去可得
,发现形式一毛一样.然后反演回去可得![]()
未完待续。
圆方树:
基础是一棵仙人掌。什么是仙人掌呢,就是说连通图中的每一条边都最多只在一个环中。
对于每个环中的点,我们新建一个方点,把它们彼此间的连边删去,并且每个点都连向那个方点。
我们称原图中的点叫圆点。
这样仙人掌变成了一棵圆方树。
圆方树有几个显然的性质:
1、方点不会直接和方点相连。
2、它是一棵无根树(即无论钦定哪个点为根,它的形态都是一样的。
3、令仙人掌中的根节点为p,节点q的子仙人掌的定义为:删去p到q的所有简单路径(即不重复经过一个点的路径),q所在的连通块的点集。我们发现,节点q的子仙人掌就是圆方树中节点p的子树(自己画图可证)
线段树优化连边:
我们要令区间[a,b]中的每个点与区间[c,d]中的每个点连边。如果是暴力的连边需要枚举每个点对,我们希望进行优化。
建立两棵线段树,一棵叫入树,一棵叫出树。都是一样的结构。作用顾名思义。
入树中每个点都向它两个儿子连零边,出树中每个点都向它父亲连零边。
至于为什么是这样子的,想想我现在能够到一个区间,是不是自然能够到它的子区间?
我现在要出发,我从我的父亲区间出发,那个路程是不是也没有问题呢?
相反 我能到一个区间,不一定能够到它的父亲区间,因此入树不往上连边。
我能从一个区间出发,能代表我能从它的父亲区间出发吗?因此出树不往下连边。
然后入树中每个点都向出树中的对应节点连零边(进入改点之后自然能从改点出)。
至于题目给出的区间,找到线段树上对应的节点,从出树连向入树。
然后跑dij。
点分治:
核心思想是每次找到一个重心,然后钦定路径一定要经过重心,计算答案。
在从重心扩散寻找路径的途上,不要走那些曾经作为重心的点。
合并子儿子的路径要用容斥的思想,删掉同一个子儿子树中的路径两两合并的情况。


