2020牛客暑期多校训练营（第七场）A National Pandemic （树剖）

题意
给定一棵树，要求对树上节点做以下操作：

1. 给定固定的x值和w值，使树上所有的点y的权值增加w-dis[x, y]
2. 给定固定的x值，使x的权值变为min(0, x的权值)
3. 输出单点的权值

分析
对于w-dis[x, y]，我们可以简单处理一下，将其转换为w- dep[x] - dep[y] + 2 * dep[lca(x, y)], 其中w-dep[x]的值是固定的，因此我们可以每次处理时都将其累加存储， S = w - dep[x]。

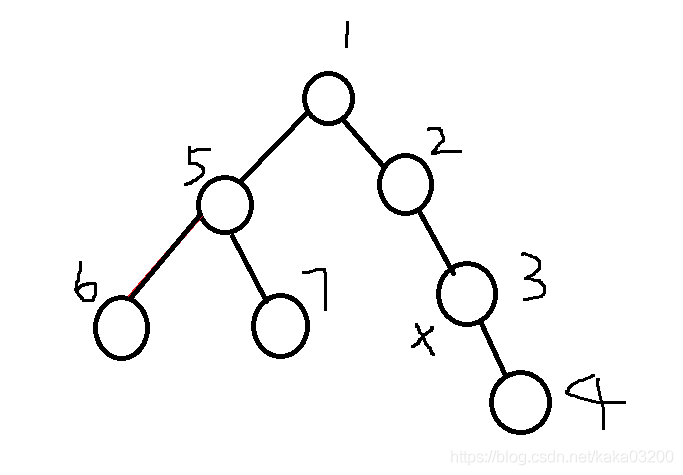
我们假设3节点为当前节点，
1.那么1的左子树的节点 5 6 7, 他们和3的lca都是节点1，因此他们节点的权值为w - deep[3] - deep[y].

2.对于1的右子树的节点 1 2 来说， 他们一定是3的lca，因此权值为w - deep[3] - deep[y] + 2*deep[y]

3.对于节点4来说， 3是他的lca，因此权值为w - deep[3] - deep[y] + 2*deep[3]

综上所述，我们发现3的lca永远都在3到根节点的链上，因此我们可以预处理3到根的路径上所有的权值+1。那为什么要这样处理呢，再往下看求节点值的公式。

对于操作3，x的权值为S - numdep[x] + 2dep[lca(x, y)], 其中num为操作1的次数，接着看lca的位置，我们将x到根的路径上权值+1，那么对于左子树无影响。对于右子树x之上的点，权值增加2dep[lca]，对于右子树x之下的节点，lca变成x，那么权值增加2dep[x]。

最后看操作2，我们只需要用delta数组记录一下x元素减少的值即可。

ac代码

#include 
using namespace std;
typedef long long ll;
#define lc u << 1
#define rc u << 1 | 1
const int N = 500100;
const int inf = 2e9;
int n, m, a, b, q, tot, T, num;
int cnt, h[N];
int siz[N], top[N], son[N], dep[N], fa[N], dfn[N], rnk[N];

struct edge {
    int to, next;
}e[N << 1];

inline void add(int u, int v) {
    e[cnt].to = v;
    e[cnt].next = h[u];
    h[u] = cnt++;
}

struct SegTree {
    ll sum[N << 2], maxx[N << 2], L[N << 2], R[N << 2], tag[N << 2];
    void push_up(int u) {
        sum[u] = sum[lc] + sum[rc];
        maxx[u] = max(maxx[lc], maxx[rc]);
    }
    void push_down(int u) {
        if (tag[u]) {
            tag[lc] += tag[u];
            tag[rc] += tag[u];
            sum[lc] += (R[lc] - L[lc] + 1) * tag[u];
            sum[rc] += (R[rc] - L[rc] + 1) * tag[u];
            tag[u] = 0;
        }
    }
    void build(int u, int l, int r) {
        L[u] = l, R[u] = r;
        maxx[u] = -inf, sum[u] = 0, tag[u] = 0;
        if (l == r) {
            sum[u] = 0;
            return;
        }
        int mid = (l + r) >> 1;
        build(lc, l, mid);
        build(rc, mid + 1, r);
        push_up(u);
    }
    int query1(int u, int ql, int qr) {
        if (ql <= L[u] && R[u] <= qr) return maxx[u];
        int mid = (L[u] + R[u]) >> 1;
        push_down(u);
        int res = -inf;
        if (ql <= mid) res = max(res, query1(lc, ql, qr));
        if (qr > mid) res = max(res, query1(rc, ql, qr));
        return res;
    }
    int query2(int u, int ql, int qr) {
        if (ql <= L[u] && R[u] <= qr) return sum[u];
        int mid = (L[u] + R[u]) >> 1;
        push_down(u);
        int res = 0;
        if (ql <= mid) res += query2(lc, ql, qr);
        if (qr > mid) res += query2(rc, ql, qr);
        return res;
    }
    void update(int u, int ql, int qr, int v) {
        if (L[u] >= ql && qr >= R[u]) {
            sum[u] += (R[u] - L[u] + 1) * v;
            tag[u] += v;
            maxx[u] = v;
            return;
        }
        push_down(u);
        int mid = (L[u] + R[u]) >> 1;
        if (ql <= mid) update(lc, ql, qr, v);
        if (qr > mid) update(rc, ql, qr, v);
        push_up(u);
    }
} st;
void dfs1(int u) {
    son[u] = -1;
    siz[u] = 1;
    for (int i = h[u]; ~i; i = e[i].next) {
        int v = e[i].to;
        if (!dep[v]) {
            dep[v] = dep[u] + 1;
            fa[v] = u;
            dfs1(v);
            siz[u] += siz[v];
            if (son[u] == -1 || siz[v] > siz[son[u]]) son[u] = v;
        }
    }
}

void dfs2(int u, int t) {
    top[u] = t;
    dfn[u] = ++tot;
    rnk[tot] = u;
    if (son[u] == -1) return;
    dfs2(son[u], t);
    for (int i = h[u]; ~i; i = e[i].next) {
        int v = e[i].to;
        if (v != son[u] && v != fa[u]) dfs2(v, v);
    }
}

int querymax(int x, int y) {
    int ret = -inf, fx = top[x], fy = top[y];
    while (fx != fy) {
        if (dep[fx] >= dep[fy])
            ret = max(ret, st.query1(1, dfn[fx], dfn[x])), x = fa[fx];
        else
            ret = max(ret, st.query1(1, dfn[fy], dfn[y])), y = fa[fy];
        fx = top[x];
        fy = top[y];
    }
    if (dfn[x] < dfn[y])
        ret = max(ret, st.query1(1, dfn[x], dfn[y]));
    else
        ret = max(ret, st.query1(1, dfn[y], dfn[x]));
    return ret;
}

ll querysum(int x, int y) {  
    ll res = 0;
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        res += st.query2(1, dfn[top[x]], dfn[x]);
        x = fa[top[x]];
    }
    if (dfn[x] > dfn[y]) swap(x, y);
    res += st.query2(1, dfn[x], dfn[y]);
    return res;
}

void solve(int x, int y, int c) {  
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        st.update(1, dfn[top[x]], dfn[x], c);
        x = fa[top[x]];
    }
    if (dfn[x] > dfn[y]) swap(x, y);
    st.update(1, dfn[x], dfn[y], c);
}
ll S, delta[N];
void init() {
    memset(son, 0, sizeof son);
    memset(dep, 0, sizeof dep);
    memset(top, 0, sizeof top);
    memset(dfn, 0, sizeof dfn);
    memset(rnk, 0, sizeof rnk);
    memset(siz, 0, sizeof siz);
    memset(delta, 0, sizeof delta);
    memset(fa, 0, sizeof fa);
    memset(h, -1, sizeof h);
    cnt = 0;
    tot = 0;
    num = 0;
    S = 0;
}

ll get_sum(int x) {
    return S - 1ll * num * dep[x] + 2 * querysum(1, x);
}

int main() {
    scanf("%d", &T);
    while (T--) {
        init();
        scanf("%d %d", &n, &m);
        for (int i = 1; i <= n - 1; i++) {
            int x, y;
            scanf("%d %d", &x, &y);
            add(x, y), add(y, x);
        }
        dep[1] = 1;
        dfs1(1);
        dfs2(1, 1);
        st.build(1, 1, n);
        for (int i = 1; i <= m; i++) {
            int op, x, w;
            scanf("%d %d", &op, &x);
            if (op == 1) {
                scanf("%d", &w);
                S += w - dep[x];
                num++;
                solve(1, x, 1);
            } 
            else if (op == 2) {
                ll ans = get_sum(x) - delta[x];
                if (ans > 0) delta[x] += ans;
            }
            else {
                printf("%lld\n", get_sum(x) - delta[x]);
            }
        }
    }
}