牛客小白月赛24题解

（其余题目还在补，涉及一些还未学的知识，补完更新）

A：最短路

https://ac.nowcoder.com/acm/contest/5158/A
这道题可以转化为如下图形

最短路径即AD1 + AD2 + D1D2弧长，但若圆心到AB之间的距离大于r即两点之间的连线与圆不相交最短距离就是AB，但这个条件不知道为什么如果直接用距离相比就只能通过%70多（大概是精度问题），所以只有用角度来判断

#include 
#include 
#include 
using namespace std;
int main()
{
    double x1,y1,x2,y2;
    cin >> x1 >> y1 >> x2 >> y2;
    double x3,y3,r;
    cin >> x3 >> y3 >> r;
    double d12 = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));/*牛能和牛可乐家之间的直线距离*/
    double d13 = sqrt((x1 - x3) * (x1 - x3) + (y1 - y3) * (y1 - y3));/*牛能到圆心的距离*/
    double d23 = sqrt((x2 - x3) * (x2 - x3) + (y2 - y3) * (y2 - y3));/*牛可乐家到圆心的距离*/
    double cos1 = (d13 * d13 + d12 * d12 - d23 * d23) / (2 * d13 * d12);/*d12与d13夹角的cos*/
    double e1 = acos(r / d13);
    double cos2 = (d12 * d12 + d23 * d23 - d13 * d13) / (2 * d12 * d23);/*d12与d23夹角的cos*/
    double e2 = acos(r / d23);
    double cos3 = (d13 * d13 + d23 * d23 - d12 * d12) / (2 * d13 * d23);/*d13与d23夹角的cos*/
    double e3 = acos(cos3);
    if(e1 + e2 > e3)
    {
        printf("%.6lf\n",d12);
        return 0;
    }
    double line = sqrt(d13 * d13 - r * r) + sqrt(d23 * d23 - r * r);/*两点到两点的切线与圆相交的切点之间距离的和*/
    double jiaodu = acos(cos3) - acos(r / d13) - acos(r / d23);/*两切点的圆心角*/
    double l = r * jiaodu;/*两切点之间的弧长*/;
    double ans = line + l;
    printf("%.6lf\n",ans);
    return 0;
}

B：组队

https://ac.nowcoder.com/acm/contest/5158/B
方法1：将输入的能量值从小到大排序，再遍历一遍，不断取最大值与最小值，如果最大值最小值之差大于k则删掉前面的最小值往后挪一位，否则就往后加一位，不断更新取最大值即可，详见代码及注释

#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
ll a[N];
int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        memset(a,0,sizeof(a));
        int n,k;
        cin >> n >> k;
        for(int i = 1; i <= n ; i++)
        {
            cin >> a[i];
        }
        sort(a + 1,a + n + 1);
        int s = 1,e = 1,ans = 0;
        while(e <= n)
        {
            e++;
            if(e > n) break;
            while(a[s] + k < a[e])/*a[e] - a[s] > k，后面一个与前面一个能量差值大于k*/
            {
                s++;/*前面的往后移*/
            }
            ans = max(ans,e - s + 1);
        }
        cout << ans << endl;
    }
    return 0;
}

方法2：采用双端队列，现将能量值排序，与前面的方法类似不过是将最小值最大值分别作为队列的队头和队尾，若队尾队头之差大于k则pop掉队头，每次取队列长度最大值即可

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
ll a[N];
ll sum[N];
int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        memset(a,0,sizeof(a));
        int n,k;
        cin >> n >> k;
        for(int i = 1; i <= n ; i++)
        {
            cin >> a[i];
        }
        sort(a + 1,a + n + 1);
        deque<int>q;
        ll ans = 0;
        for(int i = 1; i <= n ; i++)
        {
            q.push_back(a[i]);
            while(q.back() - q.front() > k)/*队尾于队头之差大于k*/
            {
                q.pop_front();
            }
            ans = max(ans,(ll)(q.size()));
        }
        cout << ans << endl;
    }
    return 0;
}

C：十面埋伏

https://ac.nowcoder.com/acm/contest/5158/C
这道题dfs，bfs都可以做，核心思想就是将士兵外围的点都标记，最后将标记的点并且在士兵外围的点设置为陷阱，这样就可以避免将士兵内部的点设置为陷阱
法1：bfs

#include 
#include 
#include 
#include 
#define Pair pair
using namespace std;
const int N = 505;
char maze[N][N];
bool vis[N][N];
int n,m;
int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
bool check(int i,int j)
{
    if(i < 1 || i > n || j < 1 || j > m)
    {
        return false;
    }
    return true;
}
int main()
{
    cin >> n >> m;
    memset(vis,false,sizeof(vis));
    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = 1; j <= m ; j++)
        {
            cin >> maze[i][j];
        }
    }
    queue<Pair>q;
    q.push(Pair{ 1,1 });
     while (!q.empty())
    {
        Pair s = q.front();
        q.pop();
        for (int i = 0; i < 4; i++)
        {
            int tx = s.first + dir[i][0];
            int ty = s.second + dir[i][1];
            if(check(tx,ty) && maze[tx][ty] == '.' && !vis[tx][ty])
            {
                vis[tx][ty] = true;
                q.push(Pair{ tx, ty });
            }

        }
    }
    for(int i = 1; i <= n ; i++)
    {
        for(int j = 1; j <= m ; j++)
        {
            if(maze[i+1][j] == '#' || maze[i-1][j] == '#' || maze[i][j+1] == '#' || maze[i][j-1] == '#')
            {
                if(vis[i][j] && maze[i][j] != '#')
                {
                    maze[i][j] = '*';
                }
            }
            cout << maze[i][j];
        }
        cout << endl;
    }
    return 0;
}

法二：dfs

#include 
#include 
using namespace std;
const int N = 505;
char maze[N][N];
bool vis[N][N];
int n,m;
int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
bool check(int i,int j)
{
    if(i < 1 || i > n || j < 1 || j > m)
    {
        return false;
    }
    return true;
}
void dfs(int i,int j)
{
    if(i == n && j == m)
    {
        return;
    }
    for(int k = 0 ; k < 4; k++)
    {
        int x_ = i + dir[k][0];
        int y_ = j + dir[k][1];
        if(check(x_,y_) && !vis[x_][y_] && maze[x_][y_] == '.')
        {
            vis[x_][y_] = true;
            dfs(x_,y_);
        }
    }
}
int main()
{
    cin >> n >> m;
    memset(vis,false,sizeof(vis));
    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = 1; j <= m ; j++)
        {
            cin >> maze[i][j];
        }
    }
    vis[1][1] = true;
    dfs(1,1);
    for(int i = 1; i <= n ; i++)
    {
        for(int j = 1; j <= m ; j++)
        {
            if(maze[i+1][j] == '#' || maze[i-1][j] == '#' || maze[i][j+1] == '#' || maze[i][j-1] == '#')
            {
                if(vis[i][j] && maze[i][j] != '#')
                {
                    maze[i][j] = '*';
                }
            }
            cout << maze[i][j];
        }
        cout << endl;
    }
    return 0;
}

F：斗兽棋

https://ac.nowcoder.com/acm/contest/5158/F
签到题，只要是牛妹吃牛牛就输出“tiangou txdy”，否则输出“tiangou yiwusuoyou”

#include 

using namespace std;
string s1 = "elephant",s2 = "tiger",s3 = "cat",s4 = "mouse";
string str1,str2;
int main()
{
    cin >> str1 >> str2;
    if((str2 == s1 && str1 == s2) || (str2 == s2 && str1 == s3) || (str2 == s3 && str1 == s4) || (str2 == s4 && str1 == s1))
    {
        cout << "tiangou txdy" << endl;
    }
    else
    {
        cout << "tiangou yiwusuoyou" << endl;
    }
}

G：做题

签到题，将输入的时间排序，从小到大依次加，直到花费总时间大于m分钟

#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int N = 5e5 + 5;
ll a[N],ans;
int main()
{
    ll n,m;
    scanf("%lld %lld",&n,&m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%lld",&a[i]);
    }
    sort(a+1,a+1+n);
    ll sum = 0;
    for(int i = 1; i <= n ; i++)
    {
        sum += a[i];
        if(sum <= m)
        {
            ans++;
        }
        else
        {
            break;
        }
    }
    cout << ans << endl;
    return 0;
}

I：求和

https://ac.nowcoder.com/acm/contest/5158/I

J：建设道路

https://ac.nowcoder.com/acm/contest/5158/J
这道题采用了数学公式变形的方法，将(a[i] - a[j])² 转化为a[i]² + 2 a[i]a[j] + a[j]²
求的是每个数字之间差平方的和，因此不难发现上面公式的和可以转化为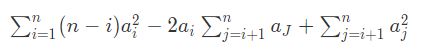
所以我们可以将后面的aj 和aj平方用前缀和处理，比如 1 2 3为(1-2)² + (1-3)² + (2-3)² 可以看做是当i = 1时，和为(3-1) * 1² + 2 * 1 * (2 + 3) + 2² + 3² 当i = 2 时，和为前面算出来的加上(3-2)² + 2 * 2 * 3 + 3²，详细步骤见代码

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 5e5 + 5;
ll a[N],sum1[N],sum2[N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d",&a[i]);
        sum1[i] = (sum1[i-1] + a[i]) % mod;
        sum2[i] = (sum2[i-1] + a[i] * a[i])% mod;
    }
    ll ans = 0;
    for(int i = 1; i <= n ; i++)
    {
        ll x1 = ((n - i) * ((a[i] * a[i]) % mod)) % mod; /*(n - i) *a[i]^2*/
        ll x2 = ((2 *a[i] % mod) * (sum1[n] - sum1[i] + mod/*可能会产生负数*/) % mod ) % mod;/*2 * a[i] * ∑j = i + 1 -> n a[j]*/
        ll x3 = (sum2[n] - sum2[i] + mod) % mod;/*∑j = i + 1 -> n a[j]^2*/
        ll x = (x1 - x2 + x3 + mod) % mod;
        ans = (ans + x) % mod;
    }
    cout << ans <<endl;
    return 0;
}