239 滑动窗口的最大值(单调队列)、279 完全平方数、283移动零到末尾、312戳气球 (动态规划)三个乘积最大,戳中间、 338比特位计数 动态规划、位运算、347前k个高频元素
- 239 滑动窗口的最大值 (单调队列)
- 240 搜索二维矩阵
- 279 完全平方数(动态规划)for(int i=1;i<=n;i++){for(int j=1;j*j<=i ;j++){
- 283移动零到末尾 ,index:表示非0数的个数
- 287寻找重复数 二分
- 297二叉树的序列化和反序列化
- 300最长上升子序列 动态规划 贪心(二分)
- 309最佳买卖股票时期含冷冻期
- 312戳气球 (动态规划)三个乘积最大,戳中间
- 322零钱兑换(总和最大,不同硬币)
- 337打家劫舍3
- 338比特位计数 动态规划、位运算(res[i] = res[i&(i-1)]+1;)
- 347前k个高频元素 hashmap频率、priorityQueue最小堆存k个
239 滑动窗口的最大值(单调队列)
窗口对应的数据结构为 双端队列 ,本题使用 单调队列 即可解决以上问题。遍历数组时,每轮保证单调队列 deque :
1、deque 内 仅包含窗口内的元素 \Rightarrow⇒ 每轮窗口滑动移除了元素 nums[i−1] ,需将 dequedeque 内的对应元素一起删除。
2、dequedeque 内的元素 非严格递减 \Rightarrow⇒ 每轮窗口滑动添加了元素 nums[j+1] ,需将 dequedeque 内所有 < nums[j + 1] 的元素删除。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums.length == 0 || k == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[nums.length - k + 1];
for(int i = 0; i < k; i++) { // 未形成窗口
while(!deque.isEmpty() && deque.peekLast() < nums[i]) deque.removeLast();
deque.addLast(nums[i]);
}
res[0] = deque.peekFirst();
for(int i = k; i < nums.length; i++) { // 形成窗口后
if(deque.peekFirst() == nums[i - k]) deque.removeFirst();
while(!deque.isEmpty() && deque.peekLast() < nums[i]) deque.removeLast();
deque.addLast(nums[i]);
res[i - k + 1] = deque.peekFirst();
}
return res;
}
}
240 搜索二维矩阵
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0) return false;
int m = 0;
int n = matrix[0].length - 1;
while (m < matrix.length && n >= 0) {
if (matrix[m][n] == target) {
return true;
} else if (matrix[m][n] > target) {
n--;
} else {
m++;
}
}
return false;
}
}
279 完全平方数和n,个数最少 动态规划
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.
首先初始化长度为n+1的数组dp,每个位置都为0
如果n为0,则结果为0
对数组进行遍历,下标为i,每次都将当前数字先更新为最大的结果,即dp[i]=i,比如i=4,最坏结果为4=1+1+1+1即为4个数字
动态转移方程为:dp[i] = MIN(dp[i], dp[i - j * j] + 1),i表示当前数字,jj表示平方数
时间复杂度:O(nsqrt(n)),sqrt为平方根
class Solution {
public int numSquares(int n) {
if(n==0) return 0;
int[] dp=new int[n+1];
for(int i=0;i<=n;i++){
dp[i]=i;
}
for(int i=1;i<=n;i++){
for(int j=1;j*j<=i ;j++){
// dp[i]=i;
dp[i]=Math.min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
}
283移动零到末尾
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作,不能拷贝额外的数组。
尽量减少操作次数。
思路:设置一个index,表示非0数的个数,循环遍历数组,
如果不是0,将非0值移动到第index位置,然后index + 1.
遍历结束之后,index值表示为非0的个数,再次遍历,从index位置后的位置此时都应该为0
public void moveZeroes(int[] nums) {
if (nums == null || nums.length <= 1) {
return;
}
int index = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
nums[index] = nums[i];
index++;
}
}
for (int i = index; i < nums.length; i++) {
nums[i] = 0;
}
}
287寻找重复数
- 寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明:
不能更改原数组(假设数组是只读的)。
只能使用额外的 O(1) 的空间。
时间复杂度小于 O(n2) 。
数组中只有一个重复的数字,但它可能不止重复出现一次。
solution 二分查找
class Solution {
public int findDuplicate(int[] nums) {
int n=nums.length;
if(nums==null || n==0 ) return 0;
int left=1,right=n;
while(left<right){
int mid = left+((right-left)>>1);
int count=0;
for(int num:nums){
if(num<=mid){
count++;
}
}
if(count>mid){
right=mid;
}
else{
left=mid+1;
}
}
return left;
}
}
297二叉树的序列化和反序列化
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
if(root == null) return null;
helperSer(sb,root);
return sb.toString();
}
public String helperSer(StringBuilder sb , TreeNode root){
if(root == null){
sb.append("#,");
return sb.toString();
}
sb.append(root.val+",");
helperSer(sb,root.left);
helperSer(sb,root.right);
return sb.toString();
}
int index = 0; //计数变量
// Decodes your encoded data to tree.
public TreeNode deserialize(String str) {
if(str == null || str == "") return null;
String[] strr = str.split(",");
return helperDe(strr);
}
public TreeNode helperDe(String[] strr){
String cur = strr[index++];
if(cur.equals("#")) return null;
TreeNode node = new TreeNode(Integer.parseInt(cur));
node.left = helperDe(strr);
node.right = helperDe(strr);
return node;
}
}
300最长上升子序列 动态规划、贪心(二分)
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
数列未必一直递增
所以所有数字都得扫描
代码如下:
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length==0) return 0;
int[] dp=new int[nums.length];//第0个长度为1
Arrays.fill(dp,1);// 最小长度就是自身1
// 第i个元素的最大子序列长度为dp[i]
for(int i=1;i<nums.length;i++){
for(int j=0;j<i;j++){
if(nums[j]<nums[i]){
dp[i]=Math.max(dp[i], dp[j]+1);
}
}
}
int res=1;
for(int i=0;i<nums.length;i++){// 再遍历一遍
res=Math.max(res,dp[i]);
}
return res;
}
}
复杂度
时:O(N^2)
O(nlogn)?可以吗
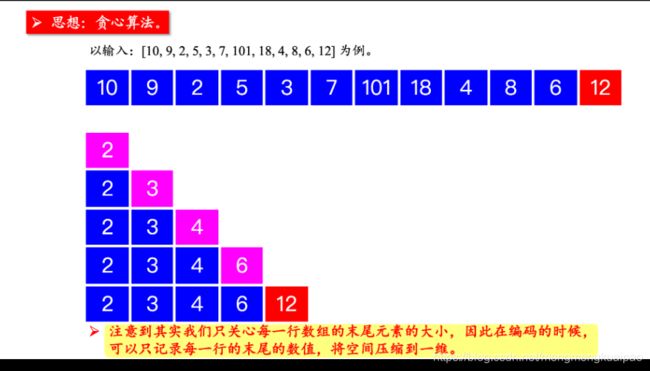
可以贪心算法
public class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
// 特判
if (len <= 1) {
return len;
}
// tail 数组的定义:长度为 i + 1 的上升子序列的末尾最小是几
int[] tail = new int[len];
// 遍历第 1 个数,直接放在有序数组 tail 的开头
tail[0] = nums[0];
// end 表示有序数组 tail 的最后一个已经赋值元素的索引
int end = 0;
for (int i = 1; i < len; i++) {
// 【逻辑 1】比 tail 数组实际有效的末尾的那个元素还大
if (nums[i] > tail[end]) {
// 直接添加在那个元素的后面,所以 end 先加 1
end++;
tail[end] = nums[i];
} else {
// 使用二分查找法,在有序数组 tail 中
// 找到第 1 个大于等于 nums[i] 的元素,尝试让那个元素更小
int left = 0;
int right = end;
while (left < right) {
// 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
// int mid = left + (right - left) / 2;
int mid = left + ((right - left) >>> 1);
if (tail[mid] < nums[i]) {
// 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1;
} else {
right = mid;
}
}
// 走到这里是因为 【逻辑 1】 的反面,因此一定能找到第 1 个大于等于 nums[i] 的元素
// 因此,无需再单独判断
tail[left] = nums[i];
}
// 调试方法
// printArray(nums[i], tail);
}
// 此时 end 是有序数组 tail 最后一个元素的索引
// 题目要求返回的是长度,因此 +1 后返回
end++;
return end;
}
}
309最佳买卖股票时期含冷冻期
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
class Solution {
public int maxProfit(int[] prices) {
// 参考309 团灭股票方法
// dp[i][0]=Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);
// dp[i][1]=Math.max(dp[i-1][1], dp[i-2][0]-prices[i]);
int n=prices.length;
int dp_i_0=0, dp_i_1=Integer.MIN_VALUE;
int dp_pre_0=0;
for(int i=0;i<n;i++){
int tmp=dp_i_0;// 保存昨天的
dp_i_0=Math.max(dp_i_0,dp_i_1+prices[i]);
dp_i_1=Math.max(dp_i_1, dp_pre_0-prices[i]);
dp_pre_0=tmp;// 保存的就是前天的了
}
return dp_i_0;
}
}
312戳气球
有 n 个气球,编号为0 到 n-1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。如果你戳破气球 i ,就可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后,气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
说明:
你可以假设 nums[-1] = nums[n] = 1,但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
示例:
输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 315 + 358 + 138 + 181 = 167
solution动态规划
以两个数作为左右端点,找出最优解中它们中间那个戳破的气球,中间这个气球把整个队列分为了2部分,要想让中间这个气球和2个端点靠在一起,就需要先把分开的2部分的气球戳破。 dp[i][j]表示i~j最大值,i,j不戳破。 比如k气球在i,j之间时(i,k,j)被戳破,那么要先戳破i,k、k,j之间的气球,所以
dp[i][j]=dp[i][k]+dp[k][j]+nums[i]*nums[k]*nums[j]
class Solution {
public int maxCoins(int[] nums) {
// 在首尾分别插入一个权重为1的气球,是运算更简便
int n = nums.length;
int[]arr = new int[n+2];
arr[0]=arr[n+1]=1;
for (int i = 1; i <=n ; i++) {
arr[i] = nums[i-1];
}
// dp[i][j]表示戳破i~j之间的气球获得的最大值
// 已经初始化了dp[0][0]=dp[n+1][n+1]=0
int [][]dp = new int[n+2][n+2];
// 倒序迭代
// 起点
for (int l = n-1; l>=0 ; l--) {
// 终点
for (int r = l+2; r<=n+1 ; r++) {
// 遍历得到该区间的最大值
for (int k = l+1; k <=r-1 ; k++) {
dp[l][r] = Math.max(dp[l][r],dp[l][k]+dp[k][r]+arr[l]*arr[k]*arr[r]);
}
}
}
return dp[0][n+1];
}
}
322零钱兑换 不同面额总数n 最少硬币
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
class Solution {
public int coinChange(int[] coins, int amount) {
if(coins.length==0) return 0;
if(amount<0) return -1;
int[] dp =new int[amount+1];//因为最多只能为amount 都是一元
Arrays.fill(dp, amount+1);
dp[0]=0;
for(int i=0;i<=amount;i++){
for(int j=0;j<coins.length;j++){
if(amount<coins[j]) continue;
if(i-coins[j]<0) continue;
dp[i]=Math.min(dp[i], dp[i-coins[j]]+1);
}
}
return dp[amount]==amount+1? -1:dp[amount];
}
}
337打家劫舍3
lee337
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入: [3,2,3,null,3,null,1]
3
/ \
2 3
\ \
3 1
输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
示例 2:
输入: [3,4,5,1,3,null,1]
3
/
4 5
/ \ \
1 3 1
输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
思路 递归 首先要看清题 其实就是二叉树结构 不能相邻节点 就是父节点选中 不能有子节点,可以选孙子节点
在解法1和解法2中 我们使用爷爷-两个孩子-4个孙子来说明问题
首先来定义这个问题的状态
爷爷节点获取到最大的偷取的钱数呢
首先要明确相邻的节点不能偷,也就是爷爷选择偷,儿子就不能偷了,但是孙子可以偷
二叉树只有左右两个孩子,一个爷爷最多2个儿子,4个孙子
根据以上条件,我们可以得出单个节点的钱该怎么算
4个孙子偷的钱 + 爷爷的钱 VS 两个儿子偷的钱 哪个组合钱多,就当做当前节点能偷的最大钱数。这就是动态规划里面的最优子结构
由于是二叉树,这里可以选择计算所有子节点
4个孙子投的钱加上爷爷的钱如下
int method1 = root.val + rob(root.left.left) + rob(root.left.right) + rob(root.right.left) + rob(root.right.right)
两个儿子偷的钱如下
int method2 = rob(root.left) + rob(root.right);
挑选一个钱数多的方案则
int result = Math.max(method1, method2);
public int rob(TreeNode root) {
if (root == null) return 0;
int money = root.val;
if (root.left != null) {
money += (rob(root.left.left) + rob(root.left.right));
}
if (root.right != null) {
money += (rob(root.right.left) + rob(root.right.right));
}
return Math.max(money, rob(root.left) + rob(root.right));
}
这样效率低,想到memo[ ] 存储
我们这一步针对重复子问题进行优化,我们在做斐波那契数列时,使用的优化方案是记忆化,但是之前的问题都是使用数组解决的,把每次计算的结果都存起来,下次如果再来计算,就从缓存中取,不再计算了,这样就保证每个数字只计算一次。
由于二叉树不适合拿数组当缓存,我们这次使用哈希表来存储结果,TreeNode当做key,能偷的钱当做value
修改一下上面的代码可得:
class Solution {
HashMap<TreeNode, Integer> map = new HashMap<>();
public int rob(TreeNode root) {
if(root==null) return 0;
// map.put(root,0);
if(map.containsKey(root)) return map.get(root);
int money=root.val;
if(root.left!=null){
money+=(rob(root.left.left)+rob(root.left.right));
}
if(root.right!=null){
money+=(rob(root.right.left)+rob(root.right.right));
}
int res= Math.max(money, rob(root.left)+rob(root.right));
map.put(root,res);
return res;
}
}
一般人想不到的终极解法3
上面两种解法用到了孙子节点,计算爷爷节点能偷的钱还要同时去计算孙子节点投的钱,虽然有了记忆化,但是还是有性能损耗。
我们换一种办法来定义此问题
每个节点可选择偷或者不偷两种状态,根据题目意思,相连节点不能一起偷
当前节点选择偷时,那么两个孩子节点就不能选择偷了
当前节点选择不偷时,两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)
我们使用一个大小为2的数组来表示 int[] res = new int[2] 0代表不偷,1代表偷
任何一个节点能偷到的最大钱的状态可以定义为
当前节点选择不偷: 当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
当前节点选择偷: 当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数
表示为公式如下
root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) + Math.max(rob(root.right)[0], rob(root.right)[1])
root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;
代码如下:
public int rob(TreeNode root) {
int[] result = robInternal(root);
return Math.max(result[0], result[1]);
}
public int[] robInternal(TreeNode root) {
if (root == null) return new int[2];
int[] result = new int[2];
int[] left = robInternal(root.left);
int[] right = robInternal(root.right);
result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
result[1] = left[0] + right[0] + root.val;
return result;
}
338比特位计数
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
示例 1:
输入: 2
输出: [0,1,1]
示例 2:
输入: 5
输出: [0,1,1,2,1,2]
进阶:
给出时间复杂度为O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗?
要求算法的空间复杂度为O(n)。
class Solution {
public int[] countBits(int n) {
if(n==0) return new int[]{0};
int[] res = new int[n+1];
for(int i=1;i<=n;i++){
res[i] = res[i&(i-1)]+1;
}
return res;
}
}
347前k个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
你可以按任意顺序返回答案。
solution1 hashmap记录频率,优先队列最小堆存
class Solution {
public int[] topKFrequent(int[] nums, int k) {
//先统计每个数字出现的次数,这个貌似不可避免,时间复杂度为O(n)
HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
for(int i=0;i<nums.length;i++){
map.put(nums[i],map.getOrDefault(nums[i],0)+1);
}
//然后应该可以使用优先队列了,
PriorityQueue<Integer> pq = new PriorityQueue<Integer>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return map.get(o1)-map.get(o2);
}
});
for(int key:map.keySet()){
if(pq.size()<k){
pq.add(key);
continue;
}
int small = pq.peek();
if(map.get(small)<map.get(key)){
pq.poll();
pq.add(key);
}
}
int[] res =new int[pq.size()];
for(int i=0; i<res.length;i++){
res[i] = pq.poll();
}
return res;
}
}
时:nlogk