mrcrack

信息学奥赛一本通（C++版）第二部分基础算法第九章动态规划

总目录详见：https://blog.csdn.net/mrcrack/article/details/86501716

第一节动态规划的基本模型
//1258 【例9.2】数字金字塔
//动态规划，自底向上计算，找出当前节点的最大值，一步一步推到顶点2017-11-3 21:57
#include
int a[1100][1100],sum[1100][1100];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++)
            scanf("%d",&a[i][j]);
    for(j=1;j<=n;j++)sum[n][j]=a[n][j];
    for(i=n-1;i>=1;i--)
        for(j=1;j<=i;j++)
            sum[i][j]=max(sum[i+1][j]+a[i][j],sum[i+1][j+1]+a[i][j]);
    printf("%d",sum[1][1]);
    return 0;
}

//1259 【例9.3】求最长不下降序列
//提交，未通过，测试点3 答案错误
//上了题目的大当,不下降序列,两个元素值相等也属于不下降序列，
//但从题意来说两个元素相等不属下降序列，认识到这个问题，花了20分钟
//按相等也属序列来处理，修改，提交AC 2017-11-3 23:03
#include
int b[210],d[210],a[210];
int main(){
    int n,i,j,max=-999999999,k,q=0,m;
    scanf("%d",&n);
    for(i=1;i<=n;i++)scanf("%d",&b[i]);
    for(i=1;i<=n;i++){
        d[i]=1;
        for(j=1;j             if(b[j]<=b[i]&&d[j]+1>d[i])d[i]=d[j]+1;//此处写成if(b[j]d[i])d[i]=d[j]+1;
        if(d[i]>max)max=d[i],k=i;
    }
    m=max;
    a[q++]=k,i=k-1;
    while(m>1){//根据d[i]值逆向查找，
        if(d[i]==m-1&&b[i]<=b[k])a[q++]=i,k=i,m--;//此处写成 if(d[i]==m-1&&b[i]         i--;
    }
    printf("max=%d\n",max);
    for(i=q-1;i>=0;i--)
        printf("%d ",b[a[i]]);
    return 0;
}
方法二

#include
int pre[210],b[210],d[210],a[210];
void print(int k){
if(k==-1)return;
print(pre[k]);
printf("%d ",b[k]);
}
int main(){
int n,i,j,max=-999999999,k,q=0,m;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&b[i]);
for(i=1;i<=n;i++)pre[i]=-1;
for(i=1;i<=n;i++){
d[i]=1;
for(j=1;j if(b[j]<=b[i]&&d[j]+1>d[i])pre[i]=j,d[i]=d[j]+1;//此处写成if(b[j]d[i])d[i]=d[j]+1;
if(d[i]>max)max=d[i],k=i;
}
m=max;
printf("max=%d\n",max);
print(k);
return 0;
}
//1260 【例9.4】拦截导弹(Noip1999)
//用之前洛谷p1020 导弹拦截 http://blog.csdn.net/mrcrack/article/details/61625530 AC代码提交，竟然测试点6答案错误，惊愕
//a[]导弹数 b[]最长下降子序列拦截系统 c[]最长上升子序列
//加上等于，提交，测试点3,8答案错误，这下放心，测试点6安全通过，
//仔细想了想，最少能拦截1枚导弹，最少需要一套系统，故mx=-1错误
//提供一组测试样例
//输入：
//123
//输出：
//1
//1
//修改，提交，测试点3答案错误
//突然想到一组测试数据
//输入：
//1 1 1 1 1
//输出：
//5
//1
//修改，提交AC，该题的数据确实比洛谷要精进许多。
#include
int a[1100],b[1100],c[1100];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int cnt=0,i,j,mx=1;//此处写成mx=-1
    while(scanf("%d",&a[cnt++])!=EOF)
    for(i=0;i         b[i]=1;
        for(j=0;j             if(a[j]>=a[i]&&b[j]+1>b[i])//通过测试点6 if(a[j]>=a[i]&&b[j]+1>b[i]) 注意等号不能省
                b[i]=b[j]+1;
        mx=max(mx,b[i]);
    }
    printf("%d\n",mx);
    mx=1;//此处写成mx=-1
    for(i=0;i         c[i]=1;
        for(j=0;j             if(a[j]c[i])//再次测试，发现此处if(a[j]<=a[i]&&c[j]+1>c[i])，要通过测试点3，必须将=号去除//通过测试点6 if(a[j]<=a[i]&&c[j]+1>c[i]) 注意等号不能省
                c[i]=c[j]+1;
        mx=max(mx,c[i]);
    }
    printf("%d\n",mx);
    return 0;
}

//1261 【例9.5】城市交通路网
//很想用Dijkstra 或是 floyd算法，但看到题目要求，想想还是算了
//翻看了一些代码，发现就是Dijkstra算法，想想也是，要是能很快想出的算法，也就不需要研究了。
//决定用Dijkstra算法，采用邻接表方式，也算是一个挑战吧。
//有向图，打印途经路径遇到困难，
//打印路径，http://blog.csdn.net/yuanba_xs/article/details/54799157参考该文，看了代码，很快就有感觉了。
//修改代码，提交AC 2017-11-4
//https://wenku.baidu.com/view/0ab0456883d049649a66588a.html 此文介绍得不错，摘抄如下：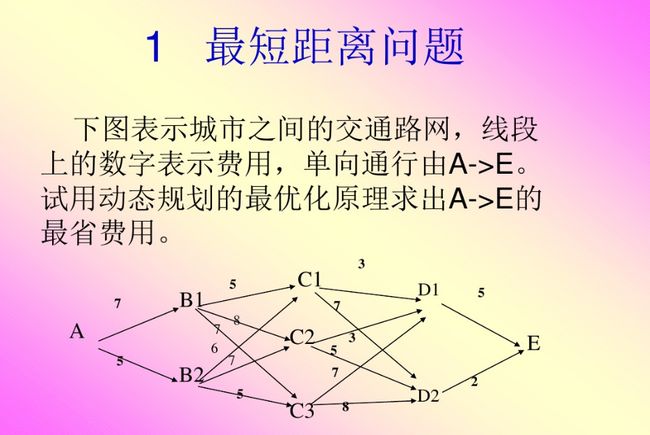

//抽空进行研究。
#include
#include
#define INF 999999999
int cnt=0,head[1000],n,d[1000],vis[1000],path[1000],pre[1000];
struct node{
    int to,next,w;
}e[10000];
void add_edge(int u,int v,int w){
    cnt++,e[cnt].to=v,e[cnt].w=w,e[cnt].next=head[u],head[u]=cnt;
}
void print(int k){//递归打印路径
    if(k==-1)return;
    print(pre[k]);
    printf("%d ",k+1);
}
int main(){
    int i,j,w,b,t,k,v,min,q=0,x;//b边
    memset(head,0,sizeof(head));
    memset(vis,0,sizeof(vis));
    scanf("%d",&n);
    for(i=0;i         for(j=0;j             scanf("%d",&w);
            if(w)add_edge(i,j,w);
        }
    for(i=0;i     d[0]=0,t=n-1,vis[0]=1,pre[0]=-1;
    for(b=head[0];b;b=e[b].next)d[e[b].to]=e[b].w;
    while(t--){//一个点查询一次
        min=INF;
        for(i=0;i             if(vis[i]==0&&d[i]         vis[k]=1;
        for(b=head[k];b;b=e[b].next){
            v=e[b].to,w=e[b].w;//漏了该句 w=e[b].w 查了好久
            if(vis[v]==0&&d[v]>d[k]+w)d[v]=d[k]+w,pre[v]=k;
        }
    }
    printf("minlong=%d\n",d[n-1]);
    k=n-1;
    print(k);
    return 0;
}

//1262 【例9.6】挖地雷
//本想深度优先遍历，发现n<=200，暂放弃。
//画图模拟了一下，发现是一维线性动态规划。
//样例通过，提交AC，太佩服自己了，此题独立思考，编写，提交AC，没有参考任何资料，（期间一度想看看他人代码，忍住了），水平就是这样提高的
//2017-11-25 15:15
#include
#include
int a[210][210],w[210],d[210],pre[210];//d[i]表示挖到i点的最大值
void print(int k){
    if(k==0)return;
    print(pre[k]);
    if(pre[k]==0)printf("%d",k);
    else printf("-%d",k);
}
int main(){
    int i,j,n,max=0,k;
    memset(a,0,sizeof(a)),memset(pre,0,sizeof(pre));
    scanf("%d",&n);
    for(i=1;i<=n;i++)scanf("%d",&w[i]);
    while(scanf("%d%d",&i,&j)&&i&&j){
        a[i][j]=1;//有向图
    }
    for(i=1;i<=n;i++)d[i]=w[i];
    for(i=1;i<=n;i++){
        for(j=1;j<=n;j++)
            if(a[j][i]&&d[j]+w[i]>d[i])//此处写成if(a[j][i]&&d[j]+w[j]>d[i])眼高手低//请注意，有向图,j->i
                d[i]=d[j]+w[i],pre[i]=j;//此处写成 d[i]=d[j]+w[j];
        if(d[i]>max)max=d[i],k=i;
    }
    print(k);
    printf("\n%d",max);
    return 0;
}

//1263 【例9.7】友好城市
//该题破题很难，觉得手足无措
//瞟了一眼http://blog.csdn.net/ruruoran/article/details/38533337看到
//先以南岸排升序。处理数据时用求最长上升子序列的方法，就没再往下看了
//模拟了样例，立马有了思路。
//看了数据范围，N<=5000，冒泡排序应该可以接受，选择原因是代码容易写
//样例通过，提交AC,害怕的TLE没有出现
#include
struct node{
    int a,b;
}q[5100],q_t;
int d[5100];//北岸最长上升子序列
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j,mx=-1;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d%d",&q[i].a,&q[i].b);
    for(i=1;i<=n;i++)//南岸自小到大排序，若相等，北岸自小到大排序
        for(j=i+1;j<=n;j++)
            if(q[i].a>q[j].a)
                q_t=q[i],q[i]=q[j],q[j]=q_t;
            else if(q[i].a==q[j].a)
                if(q[i].b>q[j].b)
                    q_t=q[i],q[i]=q[j],q[j]=q_t;
    for(i=1;i<=n;i++){
        d[i]=1;
        for(j=1;j             if(q[j].b<=q[i].b&&d[j]+1>d[i])
                d[i]=d[j]+1;
        mx=max(mx,d[i]);//此处写成mx=(mx,d[i]);，查了半天，真是犯晕了
    }
    printf("%d",mx);
    return 0;
}

//1264 【例9.8】合唱队形

http://blog.csdn.net/mrcrack/article/details/61625530

2.//p1091 合唱队形

NOIP 2004 提高组复赛 chorus 合唱队形

1.读完题目，可以理解为处理最长上升子序列，最长下降子序列。

2.上述思路闪过后，开始模拟样例，看看能不能整合思路。

3.顺序的上升子序列，逆序的上升子序列。

4.模拟了样例，如下：

5.思路如上，顺序上升，逆序上升，对应位置求和，找出最大值，总数-最大值+1即为答案。

6.开始编码。样例测试通过，提交AC。一次性成功。

附上AC代码，编译环境Dev-C++4.9.9.2

#include
int a[100+10],b[100+10],c[100+10];
int max=1;
int main(){
    int n,i,j;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(i=1;i<=n;i++){//顺序，最长上升子序列
        b[i]=1;
        for(j=1;j             if(a[j]                 if(b[j]+1>b[i])
                    b[i]=b[j]+1;
            }
    }
    for(i=n;i>=1;i--){//逆序，最长上升子序列
        c[i]=1;
        for(j=n;j>i;j--)
            if(a[j]                 if(c[j]+1>c[i])
                    c[i]=c[j]+1;
    }
    for(i=1;i<=n;i++)
        if(max             max=b[i]+c[i];
    printf("%d\n",n-max+1);
}

2017-4-22 15:10

//1265【例9.9】最长公共子序列 2018-3-14
#include
#include
char a[1010],b[1010];
int f[1010][1010];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int i,j,len_a,len_b;
    scanf("%s%s",&a[1],&b[1]);
    len_a=strlen(&a[1]),len_b=strlen(&b[1]);
    for(i=0;i<=len_a;i++)f[i][0]=0;
    for(i=0;i<=len_b;i++)f[0][i]=0;
    for(i=1;i<=len_a;i++)
        for(j=1;j<=len_b;j++)
            if(a[i]==b[j])f[i][j]=f[i-1][j-1]+1;
            else f[i][j]=max(f[i-1][j],f[i][j-1]);
    printf("%d",f[len_a][len_b]);
    return 0;
}

//1265 【例9.9】最长公共子序列
//题目，感受，题目内容书写太烦，最好能改成让人更喜欢读，倾向于下面网站所写的书中内容的描述
//样例通过，提交AC
//此题更详细的解法可以参考http://blog.csdn.net/mrcrack/article/details/78437385
//11.3 最长公共子序列
//ALDS1_10_C:Longest Common Subsequence
#include
#include
int f[210][210];//f[i][j]字符串1 取i个元素字符串2 取j个元素对应的最长公共子序列长度
char a[210],b[210];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int i,j,len_1,len_2;
    a[0]=' ',b[0]=' ';
    scanf("%s%s",a+1,b+1);
    len_1=strlen(a)-1,len_2=strlen(b)-1;//扣除开始的' '
    for(i=1;i<=len_1;i++)f[i][0]=0;
    for(j=1;j<=len_2;j++)f[0][j]=0;
    for(i=1;i<=len_1;i++)
        for(j=1;j<=len_2;j++){
            if(a[i]==b[j])f[i][j]=f[i-1][j-1]+1;//此处写成 if(a[i]==b[i])f[i][j]=f[i-1][j-1]+1;低级错误
            else f[i][j]=max(f[i-1][j],f[i][j-1]);
        }
    printf("%d",f[len_1][len_2]);
    return 0;
}
//1266 【例9.10】机器分配
//http://blog.csdn.net/xy20130630/article/details/51753142此文代码写得够短，内容写得够简洁
//看了里面的公式，发现本人的想法还是差了一点点，不过，进步可喜。
//http://blog.csdn.net/xiaoxiaoluo/article/details/8037288此文打印公司及台数写得不错
//综上所述，解决问题，需要一个一个的来。
//采用对照代码的形式，发现问题，样例通过，提交AC。注意，该题，取最大值时，需要考虑=号
#include
#include
int f[15][20],a[15][20],out[15][20];//f[i][j]前i个公司，分配
void print(int x,int y){
    if(x==0)return;
    print(x-1,y-out[x][y]);
    printf("%d %d\n",x,out[x][y]);//此处写成 printf("%d %d\n",x,y);
}
int main(){
    int i,j,k,n,m;
    memset(f,0,sizeof(f)),memset(a,0,sizeof(a)),memset(out,0,sizeof(out));
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            for(k=0;k<=j;k++)//注意k的取值范围 ,之前写成for(k=1;k<=j;k++)
                if(f[i][j]<=f[i-1][j-k]+a[i][k]){//此处写成if(f[i][j]<=f[i-1][k]+a[i][j-k])//注意，写成if(f[i][j]                     f[i][j]=f[i-1][j-k]+a[i][k];
                    out[i][j]=k;//记录了3个关键信息i,j,k
                }
    printf("%d\n",f[n][m]);
    print(n,m);
    return 0;
}

//1281 最长上升子序列
//此题注意不能取等号
#include
int d[1100],a[1100];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j,mx=-1;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(i=1;i<=n;i++){
        d[i]=1;
        for(j=1;j             if(a[j]d[i])//此处写成 if(a[j]<=a[i]&&d[j]+1>d[i])
                d[i]=d[j]+1;
        mx=max(mx,d[i]);
    }
    printf("%d",mx);
    return 0;
}

//1282 最大子矩阵

//1224 最大子矩阵

#include
#include
int a[110][110],b[110],n;
int maxArray(int c[]){
    int d=0,i,max=-999999999;
    for(i=1;i<=n;i++){
        if(d>0)d=d+c[i];
        else d=c[i];
        if(d>max)max=d;
    }
    return max;//此处写成 return d; 出昏招，查了25分钟
}
int main(){
    int i,j,k,max=-999999999,t;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            scanf("%d",&a[i][j]);
    for(i=1;i<=n;i++){//矩阵扫描思路，1->n,2->n,3->n,4->n,......
        memset(b,0,sizeof(b));
        for(j=i;j<=n;j++){
            for(k=1;k<=n;k++)
                b[k]+=a[j][k];
            t=maxArray(b);
            if(t>max)max=t;
        }
    }
    printf("%d",max);
    return 0;
}

//https://www.cnblogs.com/GodA/p/5237061.html此文介绍得不错，摘抄如下，略做修改
//如果有一个一维数组a[n]，如何找出连续的一段，使其元素之和最大呢？
//例如有 1 2 -3 4 -2 5 -3 -1 7 4 -6 这样一个数组，那么显然 4 -2 5 -3 -1 7 4 这个子数组元素之和最大，为4+(-2)+5+(-3)+(-3)+7+4=14。为找到一维数组的最大子数组，我们可以有以下方法。

//输入数据：

11
1 2 -3 4 -2 5 -3 -1 7 4 -6

//输出数据：

//1.穷举法

#include
int a[1000];
int main(){
    int n,i,j,k,sum,max=-999999999;
    scanf("%d",&n);
    for(i=1;i<=n;i++)scanf("%d",&a[i]);
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++){
            sum=0;
            for(k=j;k<=i;k++)sum+=a[k];
            if(sum>max)max=sum;
        }
    printf("%d",max);
    return 0;
}

//2.带记忆的递推法 ,个人感觉方法应该叫前缀和
#include
int a[1000],b[1000];//b[i]前缀和,i之前元素的和，包括i元素
int main(){
    int n,i,j,k,sum,max=-999999999;
    scanf("%d",&n);
    b[0]=0;
    for(i=1;i<=n;i++)scanf("%d",&a[i]),b[i]=b[i-1]+a[i];
    for(i=1;i<=n;i++)
        for(j=0;j             sum=b[i]-b[j];
            if(sum>max)max=sum;
        }
    printf("%d",max);
    return 0;
}

//3动态规划
//我们来分析一下最优子结构，若想找到n个数的最大子段和，那么要找到n-1个数的最大子段和，这就出来了。我们用b[i]来表示a[0]...a[i]的最大子段和，b[i]无非有两种情况
//：(1)最大子段一直连续到a[i] 　(2)以a[i]为首的新的子段　。由此我们可以得到b[i]的状态转移方程：b[i]=max{b[i-1]+a[i],a[i]}。最终我们得到的最大子段和为max{b[i], 0<=i #include
int a[1000],b; //b[i]必须要选元素i，对应的最大字段和
int main(){
    int n,i,j,k,sum,max=-999999999;
    scanf("%d",&n);
    b=0;
    for(i=1;i<=n;i++){
        scanf("%d",&a[i]);
        if(b>0)b+=a[i];
        else b=a[i];//b<=0
        if(b>max)max=b;
    }
    printf("%d",max);
    return 0;
}

//1283 登山
//正序最长上升子序列，逆序最长上升子序列不考虑等号
//每个位置相加，取最大值
//样例通过，提交AC
#include
int a[1100],b[1100],c[1100];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j,mx=0;
    scanf("%d",&n);
    for(i=1;i<=n;i++)scanf("%d",&a[i]);
    for(i=1;i<=n;i++){
        b[i]=1;
        for(j=1;j             if(a[j]b[i])b[i]=b[j]+1;
    }
    for(i=n;i>=1;i--){
        c[i]=1;
        for(j=n;j>i;j--)
            if(a[j]c[i])c[i]=c[j]+1;
    }
    for(i=1;i<=n;i++)
        mx=max(mx,b[i]+c[i]-1);//b[i],c[i] i算了2次，故需-1
    printf("%d",mx);
    return 0;
}

//1284 摘花生
//动态规划公式：f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];
//样例通过，提交AC
#include
#include
int f[110][110],a[110][110];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int t,r,c,i,j;
    scanf("%d",&t);
    while(t--){
        memset(f,0,sizeof(f));
        scanf("%d%d",&r,&c);
        for(i=1;i<=r;i++)
            for(j=1;j<=c;j++)
                scanf("%d",&a[i][j]);
        for(i=1;i<=r;i++)
            for(j=1;j<=c;j++)
                f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];
        printf("%d\n",f[r][c]);
    }
    return 0;
}

//1285 最大上升子序列和
#include
int a[1100],sum[1100];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j,mx=-1;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(i=1;i<=n;i++){
        sum[i]=a[i];
        for(j=1;j             if(a[j]sum[i])
                sum[i]=sum[j]+a[i];
        mx=max(mx,sum[i]);
    }
    printf("%d",mx);
    return 0;
}

//1286 怪盗基德的滑翔翼
#include
int a[110],d[110],b[110];
int max(int a,int b){
    return a>b?a:b;
}
int f(int a[],int n){
    int i,j,mx_1=-1,mx_2=-1;
    for(i=1;i<=n;i++){//顺序方向
        d[i]=1;
        for(j=1;j             if(a[j]>a[i]&&d[j]+1>d[i])
                d[i]=d[j]+1;
        mx_1=max(mx_1,d[i]);
    }
    for(i=n;i>=1;i--){//逆序方向
        d[i]=1;
        for(j=n;j>i;j--)
            if(a[j]>a[i]&&d[j]+1>d[i])
                d[i]=d[j]+1;
        mx_2=max(mx_2,d[i]);
    }
    return max(mx_1,mx_2);
}
int main(){
    int t,i,n;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        for(i=1;i<=n;i++)scanf("%d",&a[i]);
        printf("%d\n",f(a,n));
    }
    return 0;
}

//1287 最低通行费
//一直被 "商人必须在(2N-1)个单位时间穿越出去" 这句所羁绊
//http://blog.csdn.net/snayf/article/details/70198261此文将困惑解决，摘抄如下：
//先看题目只能走（2n-1）步，不难看出只能向右和向下走，故设f[i][j]为到达（i,j）位上最省钱的花钱数，
//因只能向下与向右，故不难推出f[i][j]=min(f[i][j-1]+f[i-1][j])+a[i][j]。细节请看下面。
//看了上述文字后，代码就没往下看了，完全可以自己编了。
//该题同样，破题难啊。
//样例通过，提交未通过,测试点全部答案错误。
//将int 改成 long long,提交，未通过
//重新将long long 改成int
//使劲查啊查，发现该文代码与本人基本一致http://m.blog.csdn.net/C18854805113/article/details/70243534
//对照，发现没问题，突然发现问题所在， f[1][1]=a[1][1];//此句写成 f[1][1]=1;查了1个小时//漏了该句
//修改，提交AC 2017-11-8 21:15
#include
int f[110][110],a[110][110];
int min(int a,int b){
    return a>b?b:a;
}
int main(){
    int n,i,j;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            scanf("%d",&a[i][j]);
    f[1][1]=a[1][1];//此句写成 f[1][1]=1;查了1个小时//漏了该句
    for(i=2;i<=n;i++)f[i][1]=f[i-1][1]+a[i][1];//这样初始化不行for(i=1;i<=n;i++)f[i][1]=a[i][1];
    for(j=2;j<=n;j++)f[1][j]=f[1][j-1]+a[1][j];//这样初始化不行for(j=1;j<=n;j++)f[1][j]=a[1][j];
    for(i=2;i<=n;i++)
        for(j=2;j<=n;j++)
            f[i][j]=min(f[i-1][j],f[i][j-1])+a[i][j];
    printf("%d",f[n][n]);
    return 0;
}

//1288 三角形最佳路径问题
#include
#include
int a[110][110],d[110][110];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j;
    memset(a,0,sizeof(a));
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++)
            scanf("%d",&a[i][j]);
    for(i=n;i>=1;i--)
        for(j=1;j<=i;j++)
            d[i][j]=max(d[i+1][j]+a[i][j],d[i+1][j+1]+a[i][j]);
    printf("%d",d[1][1]);
    return 0;
}

//1289 拦截导弹
#include
int d[20],a[20];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,i,j,mx=-1;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(i=1;i<=n;i++){
        d[i]=1;
        for(j=1;j             if(a[j]>=a[i]&&d[j]+1>d[i])
                d[i]=d[j]+1;
        mx=max(mx,d[i]);
    }
    printf("%d",mx);
    return 0;
}

2017-11-25 15:15 AC 该节内容

第二节背包问题

1267：【例9.11】01背包问题更深入的讨论详见 01背包进阶

方法三

//1267：【例9.11】01背包问题
//在线测评地址http://ybt.ssoier.cn:8088/problem_show.php?pid=1267
//突然想到，01背包就是多重背包个数为1的形式
//马上编码,样例通过，提交AC。2018-12-9 10:08
//没想到，最后是多重背包统一了完全背包 01背包。收获很大，完成了统一理论，但还有些地方需想想明白
#include
#include
int w[35],c[35],s[35],f[35][210];//s[i]表示物体i的个数
int max(int a,int b){
return a>b?a:b;
}
int main(){
int m,n,i,j,k;
memset(f,0,sizeof(f));
scanf("%d%d",&m,&n);
for(i=1;i<=n;i++){
scanf("%d%d",&w[i],&c[i]);
s[i]=1;
}
for(i=1;i<=n;i++)
for(j=0;j<=m;j++)
if(j f[i][j]=f[i-1][j];
else
for(k=0;k<=s[i];k++)
if(j>=k*w[i])
f[i][j]=max(f[i][j],f[i-1][j-k*w[i]]+k*c[i]);
printf("%d\n",f[n][m]);
return 0;
}

//1267 【例9.11】01背包问题

方法一：

//1267 【例9.11】01背包问题
//二维数组
#include
#include
int w[35],c[35],f[35][210];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int m,n,i,j;
    memset(f,0,sizeof(f));
    scanf("%d%d",&m,&n);
    for(i=1;i<=n;i++)
        scanf("%d%d",&w[i],&c[i]);
    for(i=1;i<=n;i++)
        for(j=0;j<=m;j++)
            if(j>=w[i])f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+c[i]);
            else f[i][j]=f[i-1][j];
    printf("%d",f[n][m]);
    return 0;
}

方法二：

//1267 【例9.11】01背包问题

滚动数组

#include 
#include 
int w[35],c[35],f[2][210];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    	int m,n,i,j;
    	memset(f,0,sizeof(f));
    	scanf("%d%d",&m,&n);
    	for(i=1;i<=n;i++)
        	scanf("%d%d",&w[i],&c[i]);
    	for(i=1;i<=n;i++)
        	for(j=0;j<=m;j++){
        		f[i%2][j]=f[(i-1)%2][j];
            		if(j>=w[i])f[i%2][j]=max(f[(i-1)%2][j],f[(i-1)%2][j-w[i]]+c[i]);
        	}   
    	printf("%d\n",f[n%2][m]);
    	return 0;
}

滚动数组

#include 
#include 
int w[35],c[35],f[2][210];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    	int m,n,i,j,k=0;
    	memset(f,0,sizeof(f));
    	scanf("%d%d",&m,&n);
    	for(i=1;i<=n;i++)
        	scanf("%d%d",&w[i],&c[i]);
   	 for(i=1;i<=n;i++){
   	 	k^=1;//特别注意此行，容易写错位置
        	for(j=0;j<=m;j++){
        		f[k][j]=f[k^1][j];
		    	if(j>=w[i])f[k][j]=max(f[k^1][j],f[k^1][j-w[i]]+c[i]);
         	}
         }
    	printf("%d\n",f[k][m]);
    	return 0;
}

//一维数组
#include
#include
int w[35],c[35],f[210];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int m,n,i,j;
    memset(f,0,sizeof(f));
    scanf("%d%d",&m,&n);
    for(i=1;i<=n;i++)
        scanf("%d%d",&w[i],&c[i]);
    for(i=1;i<=n;i++)
        for(j=m;j>=0;j--)
            if(j>=w[i])f[j]=max(f[j],f[j-w[i]]+c[i]);
    printf("%d",f[m]);
    return 0;
}

//1267 【例9.11】01背包问题

//f[i][j]选i个物体，j是重量对应最大价值
//样例通过，提交，测试点3，9答案错误
//修改，详见代码，提交AC 2017-11-17
#include
#include
int f[40][210],w[40],c[40];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int m,n,i,j;
    memset(f,0,sizeof(f));
    scanf("%d%d",&m,&n);
    for(i=1;i<=n;i++)scanf("%d%d",&w[i],&c[i]);
    for(i=1;i<=n;i++)//此处写成 for(i=0;i<=n;i++),测试点3，9答案错误
        for(j=0;j<=m;j++)
            if(j>=w[i])f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+c[i]);
            else f[i][j]=f[i-1][j];
    printf("%d",f[n][m]);
    return 0;
}

//以下代码，用途是打印01背包中，选中的物品。供读者进行深入学习。2019-12-13
#include 
#include 
int f[40][210],w[40],c[40],g[40][210];//g[][]记录选中的物品
void print(int x,int y){//打印选中的物品
	if(x==0)return;
	print(x-1,y-g[x][y]);
	if(g[x][y])printf("%d\n",g[x][y]);
}
int main(){
    	int m,n,i,j;
    	memset(f,0,sizeof(f));
    	scanf("%d%d",&m,&n);
    	for(i=1;i<=n;i++)scanf("%d%d",&w[i],&c[i]);
    	for(i=1;i<=n;i++)
        	for(j=0;j<=m;j++){
        		f[i][j]=f[i-1][j];
            		if(j>=w[i]&&f[i][j]

 
  上述代码的输入输出数据情况如下： 
  Input:
10 4
2 1
3 3
4 5
7 9
Output:
12
2
3
4
 
  1268：【例9.12】完全背包问题 
  该题的更详细讨论，详见从01背包进化到完全背包 
  //1268：【例9.12】完全背包问题
 //在线测评地址http://ybt.ssoier.cn:8088/problem_show.php?pid=1268 
 //用 多重背包 处理 完全背包
 //一直在想 完全背包 如何 统一 多重背包
 //没想到，最后是  多重背包 统一了 完全背包
 //完全背包 转化成 多重背包 关键是 算出匹配最大容积 的个数
 //样例通过，提交AC。2018-12-8 22:41
 //很高兴，在统一 完全背包 与 多重背包的道路上，进了一步。 
 #include 
 #include 
 int w[35],c[35],s[35],f[35][210];//s[i]匹配最大容积 的个数
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int i,j,k,m,n;
     memset(f,0,sizeof(f));
     scanf("%d%d",&m,&n);
     for(i=1;i<=n;i++){
         scanf("%d%d",&w[i],&c[i]);
         s[i]=m/w[i];
     }
     for(i=1;i<=n;i++)
         for(j=0;j<=m;j++)
             if(j                 f[i][j]=f[i-1][j];
             else
                 for(k=0;k<=s[i];k++)
                     if(j>=k*w[i])
                         f[i][j]=max(f[i][j],f[i-1][j-k*w[i]]+k*c[i]);
     printf("max=%d\n",f[n][m]);
     return 0;
 } 
   
  //1268 【例9.12】完全背包问题 
  //一般思路，样例通过，提交AC 2018-1-18 
  摘自  背包问题九讲   2018-12-5 
   
  以下代码能AC。2018-12-7
#include 
#include 
int w[40],c[40],f[40][210];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int i,j,k,m,n;
    memset(f,0,sizeof(f));
    scanf("%d%d",&m,&n);
    for(i=1;i<=n;i++)
        scanf("%d%d",&w[i],&c[i]);
    for(i=1;i<=n;i++)
        for(j=0;j<=m;j++)
            if(j
 
  以下代码也能AC。2018-12-7 
  #include 
 #include 
 int w[35],v[35],f[35][210];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int m,n,i,j,k;
     memset(f,0,sizeof(f));
     scanf("%d%d",&m,&n);
     for(i=1;i<=n;i++)scanf("%d%d",&w[i],&v[i]);
     for(i=1;i<=n;i++)
         for(j=1;j<=m;j++)
             if(j             else for(k=1;k*w[i]<=j;k++)
                 f[i][j]=max(f[i-1][j],f[i][j-k*w[i]]+k*v[i]);//此处写成 f[i][j]=max(f[i][j],f[i][j-k*w[i]]+v[i]);
     printf("max=%d",f[n][m]);
     return 0;
 } 
  //1268 【例9.12】完全背包问题
 //等同于01背包的做法
 //样例通过，提交，只有测试带点7,8答案正确
 //参照http://blog.csdn.net/ruruoran/article/details/38615425进行修改
 //要从数学模拟角度进行说明
 //提交，AC 2017-11-18 10:38
 #include 
 #include 
 int f[40][210],w[40],c[40];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int m,n,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&m,&n);
     for(i=1;i<=n;i++)scanf("%d%d",&w[i],&c[i]);
     for(i=1;i<=n;i++)
         for(j=0;j<=m;j++)
             if(w[i]>j)f[i][j]=f[i-1][j];
             else f[i][j]=max(f[i-1][j],f[i][j-w[i]]+c[i]);
     printf("max=%d",f[n][m]);
     return 0;
 } 
  //1268 【例9.12】完全背包问题
 //一维数组 2018-1-18 样例通过，提交AC
 #include 
 #include 
 int w[35],v[35],f[210];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int m,n,i,j,k;
     memset(f,0,sizeof(f));
     scanf("%d%d",&m,&n);
     for(i=1;i<=n;i++)scanf("%d%d",&w[i],&v[i]);
     for(i=1;i<=n;i++)
         for(j=w[i];j<=m;j++)//此处写成 for(j=1;j<=m;j++)
             f[j]=max(f[j],f[j-w[i]]+v[i]);//顺序更新，解释如下，因f[j-w[i]]需是最新数据，故必须从左往右更新，若从右往左更新，左边的数据是旧的，但右侧数据需要用最新的左侧数据，故右侧数据不对。理解这句花了好长时间，持续思考时间超过一个月，总算有收获。2018-1-18 请注意完全背包，需自左向右更新。
     printf("max=%d",f[m]);
     return 0;
 } 
  1269 【例9.13】庆功会   更深入的讨论详见01背包进阶到多重背包 
  滚动数组，易于理解2019-12-25 21:48 
  //多重背包
#include 
int f[2][6010],v[505],w[505],s[505],n,m;
int max(int a,int b){
	return a>b?a:b;
}
int main(){
	int i,k,j;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)scanf("%d%d%d",&v[i],&w[i],&s[i]);
	for(i=1;i<=n;i++)
		for(k=0;k<=s[i];k++)
			for(j=k*v[i];j<=m;j++)
				f[i%2][j]=max(f[i%2][j],f[(i-1)%2][j-k*v[i]]+k*w[i]);//此处错写成f[i%2][j]=f[(i-1)%2][j],f[i%2][j]=max(f[i%2][j],f[(i-1)%2][j-k*v[i]]+k*w[i]);
	printf("%d\n",f[n%2][m]);
	return 0;
} 
  //1269 【例9.13】庆功会
 //多重背包。
 //在线测评地址http://ybt.ssoier.cn:8088/problem_show.php?pid=1269
 //采用完全背包写法，提交30分，百思不得其解，搜遍网络，没有满意的文章，铺天盖地一维数组写法
 //而最接近思维的二维数组写法一直不得而见，无奈，只能从数据角度入手。
 //以下为多重背包的完全背包写法，只有30分,提供给读者。2018-12-7
 //提供一组测试数据
  输入 
  5 10      
 6 59 9
 5 62 0  
 7 46 9  
 1 21 5
 5 15 1  
  输出 
  143 
  
 //发现问题， 
   
  //马上 for(k=0;k<=s[i]&&k*v[i]<=j;k++)//此处写成 for(k=1;k<=s[i]&&k*v[i]<=j;k++) 
  //继续测试数据，又发现问题 
   
  //感觉 for(k=0;k<=s[i]&&k*v[i]<=j;k++) 中的 &&k*v[i]<=j画蛇添足了
 //仔细想了细节，f[i][j]一直在f[i-1][j],f[i][j], f[i-1][j-k*v[i]]+k*w[i]之间进行更新
 //故 f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);//此处写成f[i][j]=max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i]);
 //自个举的例子通过，提交AC.2018-12-7
 //真不容易啊，耗去整整半天时间。 不过映像更深了。值，回头要将完全背包全部更新。
 //以下为AC代码。
 #include 
 #include 
 int v[510],w[510],s[510],f[510][6100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,m,i,j,k;
     memset(f,0,sizeof(f));
     scanf("%d%d",&n,&m);
     for(i=1;i<=n;i++)
         scanf("%d%d%d",&v[i],&w[i],&s[i]);
     for(i=1;i<=n;i++)
         for(j=0;j<=m;j++)
             if(j                 f[i][j]=f[i-1][j];
             else{
                 for(k=0;k<=s[i];k++)////此处写成&&k*v[i]<=j画蛇添足了 for(k=1;k<=s[i]&&k*v[i]<=j;k++)
                     if(j>=k*v[i])
                         f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);//此处写成f[i][j]=max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i]);
             }
     printf("%d\n",f[n][m]);
     return 0;
 } 
  //1269 【例9.13】庆功会
 //多重背包。
 //在线测评地址http://ybt.ssoier.cn:8088/problem_show.php?pid=1269
 //采用完全背包写法，提交30分，百思不得其解，搜遍网络，没有满意的文章，铺天盖地一维数组写法
 //而最接近思维的二维数组写法一直不得而见，无奈，只能从数据角度入手。
 //以下为多重背包的完全背包写法，只有30分,提供给读者。2018-12-7
 #include 
 #include 
 int v[510],w[510],s[510],f[510][6100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,m,i,j,k;
     memset(f,0,sizeof(f));
     scanf("%d%d",&n,&m);
     for(i=1;i<=n;i++)
         scanf("%d%d%d",&v[i],&w[i],&s[i]);
     for(i=1;i<=n;i++)
         for(j=0;j<=m;j++)
             if(j                 f[i][j]=f[i-1][j];
             else{
                 for(k=1;k<=s[i]&&k*v[i]<=j;k++)
                     f[i][j]=max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i]);
             }
     printf("%d\n",f[n][m]);
     return 0;
 } 
  //1269 【例9.13】庆功会
 //http://blog.csdn.net/rechard_chen/article/details/38589803比较喜欢此文的思路，摘抄如下：
 //这个题其实完全背包差不多的性质；只不过完全背包的物品的个数是无限的，而这一题是有限制的。
 //采用一维数组，故从大到小开始处理
 //样例通过，提交AC 2017-12-27
 #include 
 int v[510],w[510],s[510],f[6100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,m,i,j,k;
     scanf("%d%d",&n,&m);
     for(i=1;i<=n;i++)scanf("%d%d%d",&v[i],&w[i],&s[i]);
     for(i=1;i<=n;i++)
         for(j=m;j>=0;j--)
             for(k=0;k<=s[i];k++)
                 if(j-k*v[i]>=0)
                     f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
     printf("%d",f[m]);
     return 0;
 }
 //1270：【例9.14】混合背包
 //在线测评地址http://ybt.ssoier.cn:8088/problem_show.php?pid=1270 
 //01背包 完全背包 均可 归结为 多重背包
 //样例通过，提交AC。完成了统一。2018-12-10 12:40 
 #include 
 #include 
 int w[35],c[35],s[35],f[35][210];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int m,n,i,j,k;
     memset(f,0,sizeof(f));
     scanf("%d%d",&m,&n);
     for(i=1;i<=n;i++){
         scanf("%d%d%d",&w[i],&c[i],&s[i]);
         if(s[i]==0)s[i]=m/w[i];//将 完全背包 转化为 多重背包 
     }
     for(i=1;i<=n;i++)
         for(j=0;j<=m;j++)
             if(j                 f[i][j]=f[i-1][j];
             else
                 for(k=0;k<=s[i];k++)
                     if(j>=k*w[i])
                         f[i][j]=max(f[i][j],f[i-1][j-k*w[i]]+k*c[i]);
     printf("%d\n",f[n][m]);
     return 0;
 } 

 //1270 【例9.14】混合背包
 //https://www.cnblogs.com/zzyh/p/6741123.html此文思路不错，摘抄如下：
 //其实就是将三种背包合在了一起，加个if判断是怎么背包 再怎样做就可以了
 //01背包是最基础的背包 容量V 价值 重量 求V范围内价值最大的
 //多重背包是在01背包的基础上 只能取1件改成了能取多件
 //完全背包则是取无限件
 //01背包 和 多重背包是很像的
 //注意如果 容量v逆序是01和多重 这样不会重复拿取产生矛盾
 //顺序则是 完全背包了
 //可惜，上述代码，提交，未通过
 //一查题目，发现n<=30，m<=200,修改代码，提交AC
 //采用一维数组
 //样例通过，提交AC 2017-12-27
 #include 
 #include 
 int w[40],c[40],p[40],f[210];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int m,n,i,j,k;
     scanf("%d%d",&m,&n);
     for(i=1;i<=n;i++)scanf("%d%d%d",&w[i],&c[i],&p[i]);
     for(i=1;i<=n;i++)
         if(p[i]==0)//完全背包
             for(j=w[i];j<=m;j++)//顺序
                 f[j]=max(f[j],f[j-w[i]]+c[i]);
         else//01背包，多重背包
             for(k=1;k<=p[i];k++)
                 for(j=m;j>=w[i];j--)//逆序
                     f[j]=max(f[j],f[j-w[i]]+c[i]);
     printf("%d",f[m]);
     return 0;
 }
 //1271 【例9.15】潜水员
 //http://blog.csdn.net/hynu_zhizuzhe/article/details/38895781此文代码写得不错，需要进行修改
 //采用降维的01背包
 //样例通过，提交AC 2017-12-27 18:59
 #include 
 #include 
 int a[1100],b[1100],c[1100],f[30][90];
 int min(int a,int b){
     return a }
 int main(){
     int m,n,cnt,k,i,j,u,v;
     memset(f,127,sizeof(f));
     f[0][0]=0;//此句不能漏
     scanf("%d%d%d",&m,&n,&cnt);
     for(i=1;i<=cnt;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]);
     for(i=1;i<=cnt;i++)
         for(j=m;j>=0;j--)
             for(k=n;k>=0;k--){
                 u=j+a[i],v=k+b[i];
                 if(u>=m)u=m;
                 if(v>=n)v=n;
                 f[u][v]=min(f[u][v],f[j][k]+c[i]);
             }
     printf("%d",f[m][n]);
     return 0;
 }  

 //1272 【例9.16】分组背包
 //https://www.cnblogs.com/z360/p/6366074.html此文思路不错，摘抄如下：
 //这个问题变成了每组物品有若干种策略：是选择本组的某一件，还是一件都不选。
 //也就是说设f[k][v]表示前k组物品花费费用v能取得的最大权值，
 //则有f[k][v]=max{f[k-1][v]，f[k-1][v-w[i]]+c[i]|物品i属于第k组}。
 //使用一维数组的伪代码如下：
 //for 所有的组k for v=V..0
 //for 所有的i属于组k 　　　　　　
 //f[v]=max{f[v],f[v-w[i]]+c[i]} 　　
 //注意这里的三层循环的顺序，
 //“for v=V..0”这一层循环必须在“for 所有的i属于组k”之外
 //。这样才能保证每一组内的物品最多只有一个会被添加到背包中。
 //另外，显然可以对每组中的物品应用完全背包中“一个简单有效的优化”。
 //http://www.cnblogs.com/zzyh/p/6749387.html此文代码写得不错
 //样例通过，提交AC 2017-12-28 
  //若写成if(j //翻看http://ybt.ssoier.cn:8088/problem_show.php?pid=1272 测试数据，才弄白原因，原来给的数据未必是按规则出牌，提供一组测试数据以供参考
 输入： 
  178 5 4
 40 555 1
 66 333 3
 38 1594 3
 173 1840 1
 99 1186 1
   
  if(j>=w)正确输出： 
  2780 
  if(j 
  
2149 
  经过一番跟踪，弄明白了，if(j                 q=a[i][k];//物品序号 
  W[q]未必是随q单调递减，break；之后，可能还存在数据j>=w[q],但因为break;的原因，之后数据再没有尝试的机会了。上述原因，整整跟踪了两个小时，总算明白了，if(j 
  
#include 
 #include 
 int w[40],c[40],a[20][40],f[210];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int v,n,t,i,j,k,p,q;
     memset(a,0,sizeof(a));
     scanf("%d%d%d",&v,&n,&t);
     for(i=1;i<=n;i++){
         scanf("%d%d%d",&w[i],&c[i],&p);
         a[p][++a[p][0]]=i;//a[p][0]存储p组元素个数
     }
     for(i=1;i<=t;i++)
         for(j=v;j>=0;j--)
             for(k=1;k<=a[i][0];k++){
                 q=a[i][k];//物品序号
                 if(j>=w[q])f[j]=max(f[j],f[j-w[q]]+c[q]);
             }
     printf("%d",f[v]);
     return 0;
 }
 //1273 【例9.17】货币系统
 //http://blog.csdn.net/ruruoran/article/details/39503021此文代码写得不错，摘抄如下：
 //类似于完全背包
 //提交，测试点6,9,10答案错误，将int 改成long long 提交AC 2017-12-28
 //开到a[1010],f[1010]测试点6 运行错误
 #include 
 #include 
 int a[10010];
 long long f[10010];
 int main(){
     int n,m,i,j;
     scanf("%d%d",&n,&m);//漏了此句
     memset(f,0,sizeof(f));
     f[0]=1;
     for(i=1;i<=n;i++)scanf("%d",&a[i]);
     for(i=1;i<=n;i++)
         for(j=a[i];j<=m;j++)//完全背包要自小到大，此处写成 for(j=m;j>=a[i];j--)
             f[j]+=f[j-a[i]];//此处写成 f[j]=max(f[j],f[j-a[i]]+1);
     printf("%lld",f[m]);
     return 0;
 }



 //1290 采药
 //01背包
 //方法一
 //二维数组
 #include 
 #include 
 int t[110],c[110],f[110][1100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int T,M,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&T,&M);
     for(i=1;i<=M;i++)scanf("%d%d",&t[i],&c[i]);
     for(i=1;i<=M;i++)
         for(j=0;j<=T;j++)
             if(j>=t[i])f[i][j]=max(f[i-1][j],f[i-1][j-t[i]]+c[i]);
             else f[i][j]=f[i-1][j];
     printf("%d",f[M][T]);
     return 0;
 }
  
 //1290 采药
 //01背包
 //方法二
 //一维数组
 #include 
 #include 
 int t[110],c[110],f[1100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int T,M,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&T,&M);
     for(i=1;i<=M;i++)scanf("%d%d",&t[i],&c[i]);
     for(i=1;i<=M;i++)
         for(j=T;j>=0;j--)
             if(j>=t[i])f[j]=max(f[j],f[j-t[i]]+c[i]);
     printf("%d",f[T]);
     return 0;
 }
   
  //1290 采药 
    
  4.p1048 采药 
  NOIP 2005 普及组 复赛 medic 采药 
  1.样例比较简单，很快就模拟成功，该题是01背包问题。 
  2.很快编码成功，样例通过，提交10分，只对了测试点1。 
  3.一查，竟然是数组开得太小了，int f[100+10][1000+10];//1此处写成 f[100+10][100+10];修改提交AC。 
  附上AC代码，编译环境Dev-C++4.9.9.2 
  #include 
 int t[100+10],v[100+10];
 int f[100+10][1000+10];//1此处写成 f[100+10][100+10];
 int fun(int a,int b){
     if(a>b)
         return a;
     else
         return b;
 }
 int main(){
     int T,m,i,j;
     scanf("%d%d",&T,&m);
     for(i=1;i<=m;i++)
         scanf("%d%d",&t[i],&v[i]);
     for(i=0;i<=T;i++)
         f[0][i]=0;
     for(i=1;i<=m;i++)
         for(j=0;j<=T;j++)
             if(j                 f[i][j]=f[i-1][j];
             else
                 f[i][j]=fun(f[i-1][j],f[i-1][j-t[i]]+v[i]);
     printf("%d\n",f[m][T]);
 }
   
  4.优化空间 
    
  #include 
 int t[100+10],v[100+10];
 int f[1000+10];//1此处写成 f[100+10][100+10];
 int fun(int a,int b){
     if(a>b)
         return a;
     else
         return b;
 }
 int main(){
     int T,m,i,j;
     scanf("%d%d",&T,&m);
     for(i=1;i<=m;i++)
         scanf("%d%d",&t[i],&v[i]);
     for(i=0;i<=T;i++)
         f[i]=0;
     for(i=1;i<=m;i++)
         for(j=T;j>=0;j--)//1此处写成 for(j=0;j<=T;j++)
             if(j>=t[i])
                 f[j]=fun(f[j],f[j-t[i]]+v[i]);
     printf("%d\n",f[T]);
 }
 //1291 数字组合
 //01背包问题 变种，方案数，基本思路可从01背包开始。
 //样例通过，提交AC 2017-12-17 19:28
 #include 
 #include 
 int f[25][1100],a[25];//f[i][j]取前i个数，和为j的方案数
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,m,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&n,&m);
     for(i=1;i<=n;i++)scanf("%d",&a[i]),f[i][a[i]]=1;
     for(i=1;i<=n;i++)
         for(j=1;j<=m;j++)
             if(j             else f[i][j]+=f[i-1][j]+f[i-1][j-a[i]];//第i个数能放进，分成两类，f[i-1][j]一类不放，f[i-1][j-a[i]]另一类放 ,f[i][j]是本身的情况
     printf("%d",f[n][m]);
     return 0; 
    
  } 
  //1292 宠物小精灵之收服
 //http://blog.csdn.net/kerskver/article/details/53856729此文介绍得不错
 //http://blog.csdn.net/C20192419MYS/article/details/77893920?locationNum=3&fps=1此文介绍得不错 本人更偏爱此文思路及代码
 //思路摘抄如下：
 //题目解析
 //这是一道简单的二维背包——“01”背包的升级版。这道题有两个限制条件：精灵球的数量和皮卡丘的血量。这就意味着我们存状态的数组需要3维——即g[i][j][k] 表示在前i个有j个精灵球并且皮卡丘的血量为k时，能够抓到的精灵的个数。其他的和“01”背包 一样，用一个结构体数组储存每个精灵所对应的数据。
 //struct OP
 //{
 //    int ball,V;
 //}F[105];
 //接下来就是递推DP，也就是3重for循环（不会超时），分别枚举——
 //1.前i个精灵
 //2.用j个精灵球
 //3.能满足的皮卡丘的血量
 //那么状态转移方程式是什么呢？首先设置g[i][j][k] 的最小值-假设皮卡丘的血量或精灵球的数量不足以抓住第i个精灵，则 g[i][j][k]=g[i-1][j][k]。而如果可以抓住，则考虑抓和不抓两种情况，取较大值，若抓，则为 g[i-1][j-F[i].ball][k-F[i].V]。
 //别着急提交——交上去会 Time Limit Exceeded,但并不是因为作者的程序超时，而是测试机上的栈空间不够。
 //还记得 “01”背包 的内存优化吗？二维背包也一样，第一维其实是可以省略的,但是就需要注意——枚举后两维时就需要逆序枚举了。
 //样例通过，提交AC 2017-12-27
 #include 
 #include 
 struct node{
     int a,b;//a球数量，b体力伤害
 }q[110];//此处写成 q[1100]
 int f[1100][510];//此处写成f[510][110]
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,ball,value,i,j,k,ans=0;
     memset(f,0,sizeof(f));
     scanf("%d%d%d",&ball,&value,&n);//此处写成scanf("%d%d%d",&n,&ball,&value);
     for(i=1;i<=n;i++)scanf("%d%d",&q[i].a,&q[i].b);
     for(i=1;i<=n;i++)
         for(j=ball;j>=0;j--)
             for(k=value;k>=0;k--)
                 if(j>=q[i].a&&k>=q[i].b)
                     f[j][k]=max(f[j][k],f[j-q[i].a][k-q[i].b]+1);
     for(i=1;i<=value;i++)
         if(f[ball][i]==f[ball][value]){
             ans=i;
             break;
         }
     printf("%d %d",f[ball][value],value-ans);
     return 0;
 }

   
    
    
    
  //1293 买书
 //http://blog.csdn.net/clover_hxy/article/details/50151377此文代码写得不错
 //完全背包的方案总数问题
 //可以跟踪如下程序的f[i]，就能很快明白此种动态规划的写法
 //样例通过，提交AC 2017-12-26 21:50 
 #include 
 #include 
 int f[1010],v[]={10,20,50,100};
 int main(){
     int n,i,j;
     memset(f,0,sizeof(f));
     scanf("%d",&n);
     f[0]=1;
     for(i=0;i<4;i++)
         for(j=1;j<=n;j++)
             if(j>=v[i])
                 f[j]+=f[j-v[i]];
     printf("%d",f[n]);
     return 0;
 } 
 //1294 Charm Bracelet
 //01背包问题，但要用一维数组来解决，否则超出内存限制
 //样例通过，提交AC 2017-12-18 21:22
 #include 
 #include 
 int w[3600],c[3600],f[13000];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,m,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&n,&m);
     for(i=1;i<=n;i++)scanf("%d%d",&w[i],&c[i]);
     for(i=1;i<=n;i++)
         for(j=m;j>=w[i];j--)
             f[j]=max(f[j],f[j-w[i]]+c[i]);//f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+c[i])//不放 放  
     printf("%d",f[m]);
     return 0;
 } 
    
    
    
  //1295 装箱问题
 //01背包
 //方法一
 //二维数组
 #include 
 #include 
 int v[35],f[35][20100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int V,n,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&V,&n);
     for(i=1;i<=n;i++)scanf("%d",&v[i]);
     for(i=1;i<=n;i++)
         for(j=0;j<=V;j++)
             if(j>=v[i])f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+v[i]);
             else f[i][j]=f[i-1][j];
     printf("%d",V-f[n][V]);
     return 0;
 }

 //1295 装箱问题
 //01背包
 //方法二
 //一维数组
 #include 
 #include 
 int v[35],f[20100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int V,n,i,j;
     memset(f,0,sizeof(f));
     scanf("%d%d",&V,&n);
     for(i=1;i<=n;i++)scanf("%d",&v[i]);
     for(i=1;i<=n;i++)
         for(j=V;j>=0;j--)
             if(j>=v[i])f[j]=max(f[j],f[j-v[i]]+v[i]);
     printf("%d",V-f[V]);
     return 0;
 }

   
  //1295 装箱问题 
  5.//p1049 装箱问题 
  NOIP 2001 普及组 复赛 装箱问题 
  1.一眼看出01背包问题。 
  2.剩下最小体积，可以看成装载最大体积，之后总体积扣除，即得答案。 
  3.样例很快通过，提交AC。 
  附上AC代码，编译环境Dev-C++4.9.9.2 
  #include 
 int v[30+10];
 int f[30+10][20000+10];
 int fun(int a,int b){
     if(a>b)
         return a;
     else
         return b;
 }
 int main(){
     int V,n,i,j;
     scanf("%d%d",&V,&n);
     for(i=1;i<=n;i++)
         scanf("%d",&v[i]);
     for(i=0;i<=V;i++)
         f[0][i]=0;
     for(i=1;i<=n;i++)
         for(j=0;j<=V;j++)
             if(j                 f[i][j]=f[i-1][j];
             else
                 f[i][j]=fun(f[i-1][j],f[i-1][j-v[i]]+v[i]);
     printf("%d\n",V-f[n][V]);
     return 0;
 } 

 4.空间优化，采用一维数组。 
    
  #include 
 int v[30+10];
 int f[20000+10];
 int fun(int a,int b){
     if(a>b)
         return a;
     else
         return b;
 }
 int main(){
     int V,n,i,j;
     scanf("%d%d",&V,&n);
     for(i=1;i<=n;i++)
         scanf("%d",&v[i]);
     for(i=0;i<=V;i++)
         f[i]=0;
     for(i=1;i<=n;i++)
         for(j=V;j>=0;j--)
             if(j>=v[i])
                 f[j]=fun(f[j],f[j-v[i]]+v[i]);
     printf("%d\n",V-f[V]);
     return 0; 
    
  } 
    
  //1296 开餐馆
 //奇了怪，《信息学奥赛一本通(C++版)》，提供两个代码，参考程序1 AC 参考程序2 50分
 //样例通过，提交答案错误，静态阅读代码，printf("%d\n",f[a[n]]);//此处写成printf("%d\n",f[n]);，有失水准
 //样例未通过，静态检查代码， f[a[i]]=max(f[a[i-1]],f[a[m]]+f[a[i]]);//此处写成f[i]=max(f[a[i-1]],f[a[m]]+f[a[i]]);有失水准
 //修改，提交AC 2018-1-3
 #include 
 #include 
 int a[110],f[1000100];//a[]存储距离 f[]存储利润 f[i] 1-i 之间开餐馆 最多利润
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int t,i,j,n,k,m;
     scanf("%d",&t);
     while(t--){
         scanf("%d%d",&n,&k);
         a[0]=0,memset(f,0,sizeof(f));
         for(i=1;i<=n;i++)scanf("%d",&a[i]);
         for(i=1;i<=n;i++)scanf("%d",&f[a[i]]);
         for(i=1;i<=n;i++){
             m=i-1;
             while(m>0&&a[i]-a[m]<=k)m--;
             f[a[i]]=max(f[a[i-1]],f[a[m]]+f[a[i]]);//此处写成f[i]=max(f[a[i-1]],f[a[m]]+f[a[i]]);有失水准//类似01背包,f[a[i-1]] a[i]处不建餐馆，最大利润 ,f[a[m]]+f[a[i]] a[i]处建餐馆，最大利润
         }
         printf("%d\n",f[a[n]]);//此处写成printf("%d\n",f[n]);，有失水准
     }
     return 0;
 }
 2018-1-3 AC 该节内容
   
    
  第三节 动态规划经典题 
    
  //1274 【例9.18】合并石子
 //此类动态规划思想，元素量逐渐增加，递推，枚举
 //http://blog.csdn.net/u011123263/article/details/25507705此文代码写得不错
 //样例通过，提交AC 2017-12-26 18:57
 #include 
 #include 
 #define INF 999999999
 int sum[110],f[110][110];//f[i][j] i堆 与 j堆合并之后的最大值
 int min(int a,int b){
     return a }
 int main(){
     int n,i,j,k,a;
     memset(f,127,sizeof(f));//f[][]=2139062143
     scanf("%d",&n);
     sum[0]=0;
     for(i=1;i<=n;i++){
         scanf("%d",&a);
         sum[i]=sum[i-1]+a;//sum[i] 1-i元素之和
     }
     for(i=1;i<=n;i++)f[i][i]=0;
     for(i=n;i>=1;i--)
         for(j=i+1;j<=n;j++)
             for(k=i;k<=j-1;k++)//此句最难写，可以根据下面的动态转移方程分析得出 //此处写成for(k=i+1;k<=j-1;k++) 查得有点久
                 f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
     printf("%d",f[1][n]);
     return 0;
 }

   
  //1275 【例9.19】乘积最大
 //http://blog.csdn.net/fine_rose/article/details/63685548此文介绍得不错，思路摘抄如下
 //创建二维数组 f[][] ,用 f[i][j] 表示前 i 位数包含 j 个乘号所能达到的最大乘积
 //将 i 从 2 到 n 枚举，表示分割为前i位数字
 //对每一次分割再次将 a 从 1 到 min(i-1,k) 枚举，表示前 i 位中含有 a 个乘号
 //将 b 从 a 到 i - 1 进行一次枚举，表示前 i 位中含有 a 个乘号，且最后一个乘号的位置在 b 处。那么当最后一个乘号在 b 处时最大值为前 b 位中含有 a - 1 个乘号的最大值乘上 b 处之后的数字
 //因此得出了状态转移方程 f[i][a] = max(f[i][a] , f[b][a-1] * cut(b + 1,i))
 //——（cut(b + 1,i) 表示 b + 1 到 i 位数字）
 //样例通过，提交AC 2017-12-26
 #include 
 #include 
 char in[20];
 int f[20][10];//f[i][j] i个数之间，放j个乘号，对应的积的最大值
 int cut(int left,int right){//返回left到right之间的整数值
     int i,ans=0;
     for(i=left;i<=right;i++)
         ans*=10,ans+=in[i]-'0';
     return ans;
 }
 int min(int a,int b){
     return a }
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,k,i,a,b;
     memset(f,0,sizeof(f));
     scanf("%d%d%s",&n,&k,&in[1]);
     for(i=1;i<=n;i++)f[i][0]=cut(1,i);//0个乘号
     for(i=2;i<=n;i++)
         for(a=1;a<=min(i-1,k);a++)//乘号个数
             for(b=a;b                 f[i][a]=max(f[i][a],f[b][a-1]*cut(b+1,i));
     printf("%d",f[n][k]);
     return 0;
 } 
  //1276 【例9.20】编辑距离
 //该题 与 1298    计算字符串距离 思路基本雷同
 //https://www.cnblogs.com/ylyvictor/p/7791510.html此文思路写得不错，摘抄如下
 //dp大法好【手动滑稽
 //好了进入正题
 //状态：f[i][j]记录ai与bj的最优编辑距离
 //结果：f[m][n]，其中m、n分别是a、b的串长
 //初值：b串空，要删a串长个字符；a串空，要插b串长个字符
 //转移方程：当a[i]=b[j]时，f[i][j]=f[i-1][j-1]，否则，f[i][j]=min(f[i-1][j-1]+1,f[i][j-1]+1,f[i-1][j]+1)
 //说明：f[i-1][j-1]+1：改a[i]为b[j]；
 //f[i][j-1]+1：a[i]后插入b[j-1]；
 //f[i-1][j]+1：删a[i]。
 //PS：数组一定要开大点，不然会RE后几个点
 //亲身经历qaq
 //样例通过，提交,测试点5 答案错误，测试点6-10运行错误，看开题目中说的 字符串A和B的长度均小于200 是不对的
 //马上更改， #define maxn 2100//该句写成 #define maxn 210 提交AC 2018-1-7 20:46
 #include 
 #include 
 #define maxn 2100//该句写成 #define maxn 210
 char a[maxn],b[maxn];
 int f[maxn][maxn];//f[i][j] 1-i与1-j 最小编辑距离
 int min(int a,int b){
     return a }
 int main(){
     int i,j,n,m;
     scanf("%s%s",a+1,b+1);//注意此处技巧，字符串从a[1]开始而不是a[0]开始
     n=strlen(a+1),m=strlen(b+1),memset(f,0,sizeof(f));//请注意 获取 字符串长度技巧
     for(i=1;i<=n;i++)f[i][0]=i;//删除a中i个元素，需i次
     for(i=1;i<=m;i++)f[0][i]=i;//在a中添加i个元素，需i次
     for(i=1;i<=n;i++)
         for(j=1;j<=m;j++)
             if(a[i]==b[j])f[i][j]=f[i-1][j-1];//无需操作，故与之前相等
             else f[i][j]=min(f[i-1][j],min(f[i][j-1],f[i-1][j-1]))+1;//f[i-1][j] 删除a中的i元素 f[i][j-1]将b中的j元素插到a[i]后 f[i-1][j-1] 将a[i]改成b[j]
     printf("%d",f[n][m]);
     return 0;
 }

   
  //1277 【例9.21】方格取数
 //http://blog.csdn.net/yanyanwenmeng/article/details/77073629此文思路代码都写得很不错 
  //NOIP2000复赛 提高组 第四题 
   
  1. 设状态：f[i][j][h][k];//表示两条路同时走，第一条路径走到(i,j)时，第二条走到（h,k）时的最大数字和； 
  2. 初始状态：f[0][0][0][0]=0; 
      最终状态：f[n][n][n][n]; 
  3. 状态转移方程：当i==h&&j==k时，f[i][j][h][k]=max{f[i-1][j][h-1][k],f[i][j-1][h][k-1],f[i-1][j][h][k-1],f[i][j-1][h-1][k])+a[i][j];//取上上，左左，上左，左上四个方向的最大值加上当前的值； 
  当i!=h&&j!=k时，f[i][j][h][k]=max{f[i-1][j][h-1][k],f[i][j-1][h][k-1],f[i-1][j][h][k-1],f[i][j-1][h-1][k])+a[i][j]+a[h][k];//取上上，左左，上左，左上四个方向的最大值加上两条路径当前的值； 
  //一个笔误，修改了一个多小时，样例通过，提交AC 2017-12-29
 #include 
 #include 
 int a[15][15],f[15][15][15][15];//f[i][j][r][c];(i,j),(r,c)最大值
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int i,j,r,c,n,u,v,w,t1,t2;
     scanf("%d",&n);
     memset(a,0,sizeof(a)),memset(f,0,sizeof(f));
     while(scanf("%d%d%d",&u,&v,&w)&&u&&v&&w)a[u][v]=w;
     for(i=1;i<=n;i++)
         for(j=1;j<=n;j++)
             for(r=1;r<=n;r++)
                 for(c=1;c<=n;c++){
                     t1=max(f[i-1][j][r-1][c],f[i-1][j][r][c-1]);
                     t2=max(f[i][j-1][r-1][c],f[i][j-1][r][c-1]);//此处写成 t1=max(f[i][j-1][r-1][c],f[i][j-1][r][c-1]);昏招尽出，查了一个多小时
                     f[i][j][r][c]=max(t1,t2)+a[i][j];//找 f[i-1][j][r-1][c] f[i-1][j][r][c-1] f[i][j-1][r-1][c] f[i][j-1][r][c-1]中的最大值，顺序可打乱
                     if(i!=r&&j!=c)f[i][j][r][c]+=a[r][c];
                 }
     printf("%d",f[n][n][n][n]);
     return 0;
 }

 //1278 【例9.22】复制书稿(book)
 //http://blog.csdn.net/c20182030/article/details/53445204此文写得不错
 //https://www.cnblogs.com/shamman/p/7295495.html此文写得不错
 //http://blog.csdn.net/wasd6081058/article/details/7110084?locationNum=5&fps=1此文思路介绍得不错，摘抄如下
 //动态规划就是在做最优的选择，那么我们先随便做上一次选择，看看会把问题转化成什么样子（其实就是把大问题转化成小题），以赋值书稿问题为例，n个人去复制m本书，就是划分嘛，但怎么样才是最优的呢？不知道！好，那么我先尝试选择一下，一个人完成k本和m-1个人完成n-k本，问题就转换成max{f(m-1,n-k),f(1,k)},好，f(1,k)我们是知道的，而f(m-1,n-k)就是子问题了，这个子结构是最优子结构我就不证明了，而动态规划要找到最优的解，那书的划分我们就要尝试所有的可能，因此外面一定要套循环，也就是在k的所有可能里面找到min，那么这个min就是解了。
 //在解决这个问题的时候，刚入手我老是在划分第一个人的时候搞不清楚，老想这第一个人copy k本书也有可能在中间呀？就不知道怎么用动态规划来解决了，其实这完全包含在子问题里面嘛！我们要注意动态规划的解决，（应该是所有的递归）都是从顶到下的，这就意味它是有顺序的，我的这个问题就是不会找这种顺序。
 //样例通过，提交AC 2018-1-6 21:34 动态规划，动态转移方程是关键。动态规划的学习 任重而道远
 #include 
 #include 
 #define maxn 510
 int a[maxn],b[maxn],sum[maxn],f[maxn][maxn],c[maxn][maxn];//a[i]第i本书页码 b[i]第i个人 复制页面数  sum[i] 1-i本书页码数 f[i][j] 1-i个人 复制 1-j本书 最短时间
 int max(int a,int b){
     return a>b?a:b;
 }
 int min(int a,int b){
     return a }
 int main(){
     int i,j,k,m,n,max_num,t;
     scanf("%d%d",&m,&n);//m本书 n个人
     sum[0]=0,memset(f,127,sizeof(f)),memset(b,0,sizeof(b)),memset(c,0,sizeof(c));
     for(i=1;i<=m;i++)scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
     for(j=1;j<=m;j++)f[1][j]=sum[j];//一个人 复制 j本书
     for(i=2;i<=n;i++)
         for(j=1;j<=m;j++)
             for(k=i-1;k                 f[i][j]=min(f[i][j],max(f[i-1][k],sum[j]-sum[k]));//max(f[i-1][k],sum[j]-sum[k]) f[i][j]的时间由1-i中某个人的最大时间决定 //min(f[i][j],max(f[i-1][k],sum[j]-sum[k])) 在所有f[i][j]的可能结果中寻找最短时间
     max_num=f[n][m],t=n;//采用贪心算法 计算抄写 书码
     for(i=m;i>0;i--){
         if(a[i]+b[t]>max_num)t--;
         b[t]+=a[i],c[t][++c[t][0]]=i;//c[t][0]统计t人 复制的书 的数量 c[t][1]对应 t人复制书的最大序号  c[t][c[t][0]]对应 t人复制书的最小序号
     }
     for(i=1;i<=n;i++)printf("%d %d\n",c[i][c[i][0]],c[i][1]);
     return 0;
 } 
  //1279 【例9.23】橱窗布置(flower)
 //http://blog.csdn.net/u012773338/article/details/38414445此文代码和思路都写得漂亮 可惜提交，测试点1-2,4-5,8-10答案错误
 //https://www.cnblogs.com/zzyh/p/6682979.html?utm_source=itdadao&utm_medium=referral此文思路和代码都写得漂亮,代码提交AC
 //动态规划转移方程难写，但变量初始化以及变量的范围更难
 //一直测试样例未通过，输出结果如下
 //23
 //2 3 4
 //跟踪程序，发现从题中拷贝的输入数据有误，有误数据如下：
 //3 5
 //7 23 –5 –24 16
 //5 21 -4 10 23
 //-21 5 -4 -20 20
 //更正后数据如下，请仔细对照,在输入数据上，耗费了1个小时，跟踪了程序，才发现问题
 //3 5
 //7 23 -5 -24 16
 //5 21 -4 10 23
 //-21 5 -4 -20 20
 //更正输入数据后，发现程序对样例的处理，没有问题，看来 http://ybt.ssoier.cn:8088/problem_show.php?pid=1279 要对该题输入数据进行重新 输入
 //样例通过，提交AC 2018-1-9 收获，学会了变量边界计算。最优过程路径的打印，还需多练习。
 #include 
 #include 
 #define INF 999999999
 int b[110][110],a[110][110],c[110][110],d[110];//d[i]用来记录最优美学值时，f-(i-1)花所放 花瓶 位置 //c[i][j]记录i束花插在j个空瓶，对应最大美学值，i-1束花所放瓶子位置
 int main(){
     int f,v,i,j,k,max=-INF,pos;
     scanf("%d%d",&f,&v);
     for(i=1;i<=f;i++)
         for(j=1;j<=v;j++)
             scanf("%d",&a[i][j]);
     memset(b,128,sizeof(b));
     for(j=1;j<=v-(f-1);j++)b[1][j]=a[1][j];//一束花//v-(f-1)//剩下f-1束花，至少需要f-1个空瓶，至多留给1束花 v-(f-1)个空瓶
     for(i=1;i<=f;i++)//i束花
         for(j=i;j<=v-(f-i);j++)//i束花，至少需要空瓶i个，故j=i,剩下的f-i束花 至少空瓶f-i个 故 可给 i束花 支配的 空瓶 最多v-(f-i)个空瓶
             for(k=i-1;k<=j-1;k++)//i-1束花至少需要i-1个空瓶，故k=i-1,因第i-1束花必须在第i束花的左边，故第i-1束花最远可放在j-1空瓶里
                 if(b[i][j]                     b[i][j]=b[i-1][k]+a[i][j],c[i][j]=k;//c[i][j]记录i束花插在j个空瓶，对应最大美学值时，i-1束花所放瓶子位置   
     for(j=f;j<=v;j++)
         if(b[f][j]>max)
             max=b[f][j],pos=j;//因b[i][j]数据由上一层b[i-1][k]决定，故 最大值 未必出现在 b[f][v]; //pos记录 美学值 最大 对应的 最后一束 花的 位置
     printf("%d\n",max);//此处写成printf("%d\n",b[f][v]);错误  因b[i][j]数据由上一层b[i-1][k]决定，故 最大值 未必出现在 b[f][v];
     for(i=f;i>=1;i--)//从最后一束花开始遍历
         d[f-(i-1)]=pos,pos=c[i][pos];//请注意 //c[i][j]记录i束花插在j个空瓶，对应最大美学值时，i-1束花所放瓶子位置 技巧
     for(i=f;i>=1;i--)printf("%d ",d[i]);//逆序输出
     return 0;
 } 
  //1280    【例9.24】滑雪 
  2.//p1434 滑雪 
  http://blog.csdn.net/mrcrack/article/details/61625530 
    
  //难度：普及/提高- 
 //考点：输入，输出 ,深度优先遍历，记忆化搜索。  
 //适用：小学生 
 //注意：过大的数组要开到main函数的外面。 
 //提交：70分，早有预料，还是很满意的，至少深度优先搜索找最大步数，还是掌握得不错， 测试点3,5WA 测试点10 TLE 
 //int max=1;//3之前 int max=0;仔细想想第一个点就算一步。 修改此处过了测试点3,5 
 //测试点10 TLE，估计代码需要大改。
 //采用剪枝，记忆化搜索，测试点10还是TLE
 //if(step //        return;
 //    d[r1][c1]=step;//记忆
 //为了通过测试点10，程序经历大改。
 //去除了vis数组，与以往写法大有不同。因其数据，是按自大到小读取，并且采用记忆方式读取，故略去vis数组。 
 #include 
 #include 
 int a[100+10][100+10];
 int d[100+10][100+10];
 int r,c;
 int next[][2]={{-1,0},{1,0},{0,-1},{0,1}};//上 下 左 右 
 int fun(int a,int b){
     if(a>b)
         return a;
     else
         return b;
 } 
 int dfs(int step,int r1,int c1){
     int i,j,nr,nc,t=1;//请注意，初始化t=1 
     if(d[r1][c1]>0)
         return d[r1][c1];
     for(i=0;i<4;i++){
         nr=r1+next[i][0];
         nc=c1+next[i][1];
         if(nr>=1&&nr<=r&&nc>=1&&nc<=c&&a[r1][c1]>a[nr][nc]){//2此处写成a[r1][c1]>a[nr][nc]查了会
             t=fun(t,dfs(step+1,nr,nc)+1);
         }
     }
     d[r1][c1]=t;
     return t;
 }
 int main(){
     int i,j,max=1;
     memset(d,0,sizeof(d));
     scanf("%d%d",&r,&c);
     for(i=1;i<=r;i++)//1漏写了读取数据的循环 
         for(j=1;j<=c;j++)
             scanf("%d",&a[i][j]);
     for(i=1;i<=r;i++)
         for(j=1;j<=c;j++){
             max=fun(max,dfs(1,i,j));//3此处写成 max=(max,dfs(1,i,j));查了会 
         }
     printf("%d\n",max);
     return 0;
 } 
    
  //1297 公共子序列
 //1265 【例9.9】最长公共子序列
 //题目，感受，题目内容书写太烦，最好能改成让人更喜欢读，倾向于下面网站所写的书中内容的描述
 //样例通过，提交AC
 //此题更详细的解法可以参考http://blog.csdn.net/mrcrack/article/details/78437385
 //11.3 最长公共子序列
 //ALDS1_10_C:Longest Common Subsequence
 //样例通过，提交AC 2017-12-28 21:19
 #include 
 #include 
 int f[210][210];//f[i][j]字符串1 取i个元素 字符串2 取j个元素 对应的最长公共子序列长度
 char a[210],b[210];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int i,j,len_1,len_2;
     while(scanf("%s%s",a+1,b+1)!=EOF){
         a[0]=' ',b[0]=' ';
         len_1=strlen(a)-1,len_2=strlen(b)-1;//扣除开始的' '
         for(i=1;i<=len_1;i++)f[i][0]=0;
         for(j=1;j<=len_2;j++)f[0][j]=0;
         for(i=1;i<=len_1;i++)
             for(j=1;j<=len_2;j++){
                 if(a[i]==b[j])f[i][j]=f[i-1][j-1]+1;//此处写成 if(a[i]==b[i])f[i][j]=f[i-1][j-1]+1;低级错误
                 else f[i][j]=max(f[i-1][j],f[i][j-1]);
             }
         printf("%d\n",f[len_1][len_2]);
     }
     return 0;
 } 
  //1298 计算字符串距离
 //http://blog.csdn.net/July_xunle/article/details/70290836此文介绍得不错，思路摘抄如下：
 //1.f[i][j]代表a字符串前i个字符和b字符串前j个字符改动次数;
 //2.当i等于0时，需要改动j次，j等于0时，需要改动i次，即f[0][j]=j,f[i][0]=i;
 //3.当a[i]=b[j]时，不需要改动，即f[i][j]=f[i-1][j-1];
 //4.当a[i]!=b[j]时，有三种改动方式：改成一样，删a[i]，删b[j]，即得f[i][j]=min(f[i-1][j-1],f[i-1][j],f[i][j-1])+1;
 //http://blog.csdn.net/just_young/article/details/43113327此文思路讲解不错，摘抄如下 
  这道题的时间限制是1秒，但处理的字符串长度可能达到1000，所以如果使用递归的话，则必然超时。因此，可采用动态规划的方法，构造一个二维数组，数组的“长”和“宽”分别是两个字符串的长度。 
  以题中的一个例子举例，字符串a=“jlknm”，b=“mnklj”，则可构造一个6×6的二维数组array，并将二维数组的第一行和第一列初始化为如下，因为一个空字符串和任意一个字符串的距离始终为该字符串的长度。 
    
   
    
  用两层for循环遍历两个字符串a、b（i和j从1开始取值），对比每一个字符a[i-1]和b[j-1]，若两个字符相等，即a[i-1] == b[j-1]，则不增加距离，因此对应的数组array[i][j]=array[i-1][j-1]；若两个字符不相等，则可删除a[i-1]这个字符、删除b[j-1]这个字符，或修改a[i-1]使它与b[i-1]相等。array[i][j]取这三种方法的最小值。选择修改，则array[i][j] = 1 + array[i-1][j-1]，若选择删除a[i-1]，则array[i][j] = 1 + array[i-1][j]，若选择删除b[i-1]，则array[i][j] = 1 + array[i][j-1]。运用这个方法，可将二维数组填满，如下图所示。 
   
  最后，取这个数组的最后一个元素4，即为答案。 
  
 //样例通过，提交AC 2017-12-31 22:51
 //感觉代码写得挺别扭，字符数组与f[][]数组存在错位关系，马上进行修改,提交，样例通过2018-1-1 9:05
 #include 
 #include 
 char a[1100],b[1100];//此处写成 char a[1100],b[1100],f[1100][1100];笔误坏事
 int f[1100][1100];
 int min(int a,int b){
     return a }
 int main(){
     int n,i,j,lena,lenb;
     scanf("%d",&n);
     while(n--){
         scanf("%s%s",a+1,b+1);//请注意此处技巧 2018-1-1
         lena=strlen(a+1),lenb=strlen(b+1);//请注意此处技巧 2018-1-1
         for(i=0;i<=lena;i++)f[i][0]=i;
         for(j=0;j<=lenb;j++)f[0][j]=j;
         for(i=1;i<=lena;i++)
             for(j=1;j<=lenb;j++)
                 if(a[i]==b[j])f[i][j]=f[i-1][j-1];
                 else f[i][j]=min(min(f[i-1][j-1],f[i-1][j]),f[i][j-1])+1;
         printf("%d\n",f[lena][lenb]);
     }
     return 0;
 }
 //1299 糖果
 //http://blog.csdn.net/clove_unique/article/details/50171355此文代码和思路都不错，思路摘抄如下：
 //Dzx的选择是2+3+4+5=14，这样糖果总数是7的倍数，并且是总数最多的选择。
 //这道题是背包的一个变形，背包的体积需要%一个数。
 //刚开始的思路是写一个恰放入的背包，然后枚举一下，但是发现那样的话体积的最大值达到了10^8，无论是时间还是空间都无法承受。
 //那么考虑一下优化。其实%已经给我们提供了一个思路，那就是把体积缩小到需要%的这个正整数。
 //f[i][j]表示前i个物品体积%k为j的最优值，我们可以得到状态转移方程。注意每一次都要更新，因为每个数%k的值是不确定的。
 //https://www.cnblogs.com/candy99/p/5828055.html此文代码写得最接近01背包 
    
  //样例通过，提交AC 该题还是不理解，在初始化上，要好好模拟数据生成过程。 
    
  //样例数据生成过程如下所示： 
  f[0][0]=0 f[0][6]=-999999999 a[1]=1 f[1][0]=0
 f[0][1]=-999999999 f[0][0]=0 a[1]=1 f[1][1]=1
 f[0][2]=-999999999 f[0][1]=-999999999 a[1]=1 f[1][2]=-999999998
 f[0][3]=-999999999 f[0][2]=-999999999 a[1]=1 f[1][3]=-999999998
 f[0][4]=-999999999 f[0][3]=-999999999 a[1]=1 f[1][4]=-999999998
 f[0][5]=-999999999 f[0][4]=-999999999 a[1]=1 f[1][5]=-999999998
 f[0][6]=-999999999 f[0][5]=-999999999 a[1]=1 f[1][6]=-999999998
 f[1][0]=0 f[1][5]=-999999998 a[2]=2 f[2][0]=0
 f[1][1]=1 f[1][6]=-999999998 a[2]=2 f[2][1]=1
 f[1][2]=-999999998 f[1][0]=0 a[2]=2 f[2][2]=2
 f[1][3]=-999999998 f[1][1]=1 a[2]=2 f[2][3]=3
 f[1][4]=-999999998 f[1][2]=-999999998 a[2]=2 f[2][4]=-999999996
 f[1][5]=-999999998 f[1][3]=-999999998 a[2]=2 f[2][5]=-999999996
 f[1][6]=-999999998 f[1][4]=-999999998 a[2]=2 f[2][6]=-999999996
 f[2][0]=0 f[2][4]=-999999996 a[3]=3 f[3][0]=0
 f[2][1]=1 f[2][5]=-999999996 a[3]=3 f[3][1]=1
 f[2][2]=2 f[2][6]=-999999996 a[3]=3 f[3][2]=2
 f[2][3]=3 f[2][0]=0 a[3]=3 f[3][3]=3
 f[2][4]=-999999996 f[2][1]=1 a[3]=3 f[3][4]=4
 f[2][5]=-999999996 f[2][2]=2 a[3]=3 f[3][5]=5
 f[2][6]=-999999996 f[2][3]=3 a[3]=3 f[3][6]=6
 f[3][0]=0 f[3][3]=3 a[4]=4 f[4][0]=7
 f[3][1]=1 f[3][4]=4 a[4]=4 f[4][1]=8
 f[3][2]=2 f[3][5]=5 a[4]=4 f[4][2]=9
 f[3][3]=3 f[3][6]=6 a[4]=4 f[4][3]=10
 f[3][4]=4 f[3][0]=0 a[4]=4 f[4][4]=4
 f[3][5]=5 f[3][1]=1 a[4]=4 f[4][5]=5
 f[3][6]=6 f[3][2]=2 a[4]=4 f[4][6]=6
 f[4][0]=7 f[4][2]=9 a[5]=5 f[5][0]=14
 f[4][1]=8 f[4][3]=10 a[5]=5 f[5][1]=15
 f[4][2]=9 f[4][4]=4 a[5]=5 f[5][2]=9
 f[4][3]=10 f[4][5]=5 a[5]=5 f[5][3]=10
 f[4][4]=4 f[4][6]=6 a[5]=5 f[5][4]=11
 f[4][5]=5 f[4][0]=7 a[5]=5 f[5][5]=12
 f[4][6]=6 f[4][1]=8 a[5]=5 f[5][6]=13
 14 
  2018-1-4 21:10 
    
    
   
 #include 
 #define INF 999999999//此处写成 #define INF -999999999
 int a[110],f[110][110];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int n,k,i,j;
     scanf("%d%d",&n,&k);
     for(i=1;i<=n;i++)scanf("%d",&a[i]);
     f[0][0]=0;//漏了此句  
     for(j=1;j     for(i=1;i<=n;i++)
         for(j=0;j             f[i][j]=max(f[i-1][j],f[i-1][(k+j-a[i]%k)%k]+a[i]);//此处写成f[i][j]=max(f[i-1][j],f[i][(k+j-a[i]%k)%k]+a[i]);//不放，放
     printf("%d",f[n][0]);
     return 0;
 } 
    
    
    
    
  //1300 鸡蛋的硬度
 //https://www.cnblogs.com/CXCXCXC/p/4888383.html此文，思路代码都写得不错 ,思路摘抄如下：
 //f[i][j]表示从第i层，用j个蛋尝试，所用得的最小次数，f[i][j]并不代表一定在第i层去扔，可以在1~i中任意一层扔下一个蛋，因此搞一个循环变量k，k从1~i，对于一个当前的k，这个鸡蛋扔下去有两种情况：碎和不碎。如果碎了，那此时只有j-1个蛋，要尝试1~k-1层，即是f[k-1][j-1]; 如果不碎，还有j个蛋，那么就要考虑k+1~i层，这等效于f[i-k][j]。所以f[i][j]=min(f[i][j],max(f[k-1][j-1],f[j-k][j])+1)。 
 //样例通过，提交AC 2017-12-29 22:30 
    
    
  //提供一组数据生成过程 
  //输入:10 2 
  //f[1][2]=1 f[0][1]=0 f[0][2]=0
 f[2][2]=2 f[0][1]=0 f[1][2]=1
 f[2][2]=2 f[1][1]=1 f[0][2]=0
 f[3][2]=3 f[0][1]=0 f[2][2]=2
 f[3][2]=3 f[1][1]=1 f[1][2]=1
 f[3][2]=2 f[2][1]=2 f[0][2]=0
 f[4][2]=4 f[0][1]=0 f[3][2]=2
 f[4][2]=3 f[1][1]=1 f[2][2]=2
 f[4][2]=3 f[2][1]=2 f[1][2]=1
 f[4][2]=3 f[3][1]=3 f[0][2]=0
 f[5][2]=5 f[0][1]=0 f[4][2]=3
 f[5][2]=4 f[1][1]=1 f[3][2]=2
 f[5][2]=3 f[2][1]=2 f[2][2]=2
 f[5][2]=3 f[3][1]=3 f[1][2]=1
 f[5][2]=3 f[4][1]=4 f[0][2]=0
 f[6][2]=6 f[0][1]=0 f[5][2]=3
 f[6][2]=4 f[1][1]=1 f[4][2]=3
 f[6][2]=4 f[2][1]=2 f[3][2]=2
 f[6][2]=3 f[3][1]=3 f[2][2]=2
 f[6][2]=3 f[4][1]=4 f[1][2]=1
 f[6][2]=3 f[5][1]=5 f[0][2]=0
 f[7][2]=7 f[0][1]=0 f[6][2]=3
 f[7][2]=4 f[1][1]=1 f[5][2]=3
 f[7][2]=4 f[2][1]=2 f[4][2]=3
 f[7][2]=4 f[3][1]=3 f[3][2]=2
 f[7][2]=4 f[4][1]=4 f[2][2]=2
 f[7][2]=4 f[5][1]=5 f[1][2]=1
 f[7][2]=4 f[6][1]=6 f[0][2]=0
 f[8][2]=8 f[0][1]=0 f[7][2]=4
 f[8][2]=5 f[1][1]=1 f[6][2]=3
 f[8][2]=4 f[2][1]=2 f[5][2]=3
 f[8][2]=4 f[3][1]=3 f[4][2]=3
 f[8][2]=4 f[4][1]=4 f[3][2]=2
 f[8][2]=4 f[5][1]=5 f[2][2]=2
 f[8][2]=4 f[6][1]=6 f[1][2]=1
 f[8][2]=4 f[7][1]=7 f[0][2]=0
 f[9][2]=9 f[0][1]=0 f[8][2]=4
 f[9][2]=5 f[1][1]=1 f[7][2]=4
 f[9][2]=5 f[2][1]=2 f[6][2]=3
 f[9][2]=4 f[3][1]=3 f[5][2]=3
 f[9][2]=4 f[4][1]=4 f[4][2]=3
 f[9][2]=4 f[5][1]=5 f[3][2]=2
 f[9][2]=4 f[6][1]=6 f[2][2]=2
 f[9][2]=4 f[7][1]=7 f[1][2]=1
 f[9][2]=4 f[8][1]=8 f[0][2]=0
 f[10][2]=10 f[0][1]=0 f[9][2]=4
 f[10][2]=5 f[1][1]=1 f[8][2]=4
 f[10][2]=5 f[2][1]=2 f[7][2]=4
 f[10][2]=5 f[3][1]=3 f[6][2]=3
 f[10][2]=4 f[4][1]=4 f[5][2]=3
 f[10][2]=4 f[5][1]=5 f[4][2]=3
 f[10][2]=4 f[6][1]=6 f[3][2]=2
 f[10][2]=4 f[7][1]=7 f[2][2]=2
 f[10][2]=4 f[8][1]=8 f[1][2]=1
 f[10][2]=4 f[9][1]=9 f[0][2]=0 
  2017-12-30 8:43 
  #include 
 int f[110][20];
 int max(int a,int b){
     return a>b?a:b;
 } 
 int min(int a,int b){
     return a }
 int main(){
     int n,m,i,j,k;
     while(scanf("%d%d",&n,&m)!=EOF){
         for(i=1;i<=n;i++)
             for(j=1;j<=m;j++)
                 f[i][j]=i;
         for(i=1;i<=n;i++)
             for(k=1;k<=i;k++)
                 for(j=2;j<=m;j++)
                     f[i][j]=min(f[i][j],max(f[k-1][j-1],f[i-k][j])+1);//+1表示当前尝试 
         printf("%d\n",f[n][m]);
     }
     return 0;
 }
   
  //1301 大盗阿福
 //https://www.cnblogs.com/zzyh/p/6683813.html此文介绍得不错，思路摘抄如下：
 //DP求出每一个状态的最优值，f[i]为盗窃前i家店铺的最优值，那么f[n]就是盗窃前n家店铺的最优值；
 //面临的每个抉择就是这个店铺盗还是不盗？那就从盗和不盗中选择一个最优值。
 //盗：f[i-2]+a[i];为前i-2家店铺的最优值+现在盗的店铺；
 //不盗：f[i-1]；就是前f[i-1]家店铺的最优值；
 //最后输出f[n]； 
 //思路有些类似01背包
 //样例通过，提交AC 2017-12-26 21:22 
 #include 
 int a[100100],f[100100];
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int t,i,n;
     scanf("%d",&t);
     while(t--){
         scanf("%d",&n);
         for(i=1;i<=n;i++)scanf("%d",&a[i]);
         f[0]=0,f[1]=a[1];
         for(i=2;i<=n;i++)f[i]=max(f[i-1],f[i-2]+a[i]);
         printf("%d\n",f[n]);
     }
     return 0;
 } 
  //1302 股票买卖
 //http://blog.csdn.net/jklcl/article/details/54933193此文代码写得不错，甚合心意
 //样例通过，提交AC 2017-12-30 16:48
 #include 
 #define maxn 100100
 int dp1[maxn],dp2[maxn],a[maxn];//dp1[i] 1->i第一次买卖  dp2[i] i->n 第二次买卖  因同一天可以多次买卖，故dp1[i] dp2[i]都可以取到i值
 #define INF 999999999
 int min(int a,int b){
     return a }
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int t,n,i,min_t,max_t,ans;
     scanf("%d",&t);
     while(t--){
         scanf("%d",&n);
         min_t=INF,max_t=-INF,dp1[0]=0,dp2[n+1]=0,ans=-INF;//此处写成 min_t=-INF,max_t=INF 大失水准
         for(i=1;i<=n;i++)scanf("%d",&a[i]);
         for(i=1;i<=n;i++){//从左往右，左边找最小值，右边找最大值
             min_t=min(min_t,a[i]);
             dp1[i]=max(dp1[i-1],a[i]-min_t);
         }
         for(i=n;i>=1;i--){////从右往左，左边找最小值，右边找最大值
             max_t=max(max_t,a[i]);
             dp2[i]=max(dp2[n+1],max_t-a[i]);
         }
         for(i=1;i<=n;i++)ans=max(ans,dp1[i]+dp2[i]);
         printf("%d\n",ans);
     }
     return 0;
 }

   
  //1303 鸣人的影分身
 //弄懂样例是关键
 //https://www.cnblogs.com/zzyh/p/6685427.html此文介绍得不错，摘抄如下：
 //【思路】相当于把m个相同的苹果放入n个盘子中的方法的个数
 //就将就着这个问题写思路吧 m个克拉能量相当于m个苹果，n个分身相当于n个盘子；
 //对放入的情况进行讨论
 //（1）当n>m(即当盘子个数大于苹果个数时)
 //一定有m-n个盘子空着 那么这种情况和把m个苹果放入m个盘子效果是一样的；
 //（2）当n<=m时（即当盘子个数小于苹果数）
 //分类讨论：
 //1、至少有一个盘子是空的的时候 就相当于把m个苹果放入n-1盘子中
 //2、当每个盘子都有的时候（每个盘子都有苹果了那么至少是一个吧）
 //效果就是 f(m-n,n)，把每个盘子的苹果都拿出一个；、
 //因为递归（1）是盘子数不断减少，所以当n==1时，return 1（只有一个盘子那就只有一种方法）
 //       （2）是苹果数不断减少，所以我们定义m==0时 return 1（有一种方法）；
 //样例通过，提交AC 2017-12-28 21:08
 #include 
 int dp(int m,int n){
     if(m==0||n==1)return 1;
     if(m     return dp(m,n-1)+dp(m-n,n);
 }
 int main(){
     int t,m,n;
     scanf("%d",&t);
     while(t--){
         scanf("%d%d",&m,&n);
         printf("%d\n",dp(m,n));
     }
 }

 //1304 数的划分
 //http://blog.csdn.net/u011860483/article/details/43967651此文思路写得不错，摘抄如下：
 // 根据本题要求，要将整数n划分为k部分，而且在不考虑顺序的情况下每种划分互不相同。
 //在此可以把问题抽象为一下模型：
 //有n个箱子，要把它们垒成k栋，可以假设箱子按某种满足该要求的方式已经摆好，现在从最底层每栋拿掉一个箱子，这样就只有两种情况：
 //1）之前每栋箱子的数量都多于1，则拿掉箱子后总栋数不变，则之前排列n个箱子成k栋的情况数与之后排列n-k个箱子成k栋的情况数是一样的
 //2）之前有一栋箱子的数量是1，则之前排列n个箱子成k栋的情况数与之后排列n-1个箱子成k-1栋的情况数相同
 //于是得出递推方程dp[n][k]=dp[n-j][k]+dp[n-1][k-1];
 //出口是：dp[i][1]=1;
 //http://blog.csdn.net/cacyth/article/details/51168371此文代码写得不错
 //样例通过，提交AC 2017-12-29 18:56
 #include 
 int f[10][210];
 int main(){
     int n,k,i,j;
     scanf("%d%d",&n,&k);
     f[0][0]=1;
     for(i=1;i<=k;i++)
         for(j=i;j<=n;j++)
             f[i][j]=f[i][j-i]+f[i-1][j-1];//此处写成 f[i][j]=f[i][j-i]+f[i-1][j-i];
     printf("%d",f[k][n]);
     return 0;
 }

 //1305 Maximum sum
 //http://blog.csdn.net/wangjian8006/article/details/7588345此文思路介绍得不错，摘抄如下：
 //题目大意： 对于连续的整数和的串s1和s2，s1与s2不相交，使得s1+s2最大
 //解题方法： DP。
 // lt[i]代表以第i个元素结尾的串最大值
 // rt[i]代表以第i个元素开头的串的最大值
 // 那么设置一个rtm[i]代表取后i个元素之中最大连续子串的和
 // 很显然，lt[i]=max(a[i],lt[i-1]+a[i]);
 // rt[i]=max(a[i],rt[i+1]+a[i]);
 // rtm[i]=max(rtm[i+1],rt[i]);
 //此题与poj2593一模一样，但是要将MAXV改成10010就可以A了
 //理解rtm[i]花了些时间，采用跟踪数据的办法，弄明白了，同时派生出了自己的ltm[i]
 //样例通过，提交AC 2018-1-7 17:13
 #include 
 #define maxn 50100
 int lt[maxn],ltm[maxn],rt[maxn],rtm[maxn],a[maxn];//lt[i] 以i元素结尾的值最大串 ltm[i] 1-i元素中 值最大串  rt[i] 以i元素开始的值最大串 rtm[i] i-n元素中 值最大串
 int max(int a,int b){
     return a>b?a:b;
 }
 int main(){
     int t,n,i,ans;
     scanf("%d",&t);
     while(t--){
         scanf("%d",&n);
         for(i=1;i<=n;i++)scanf("%d",&a[i]);
         lt[1]=a[1],rt[n]=a[n],ltm[1]=a[1],rtm[n]=a[n],ans=a[1];//初始化
         for(i=2;i<=n;i++)lt[i]=max(a[i],lt[i-1]+a[i]);//lt[i] 1-i中 必须选元素i的最大值
         for(i=n-1;i>=1;i--)rt[i]=max(a[i],rt[i+1]+a[i]);//rt[i] i-n中 必须选元素i的最大值
         for(i=2;i<=n;i++)ltm[i]=max(ltm[i-1],lt[i]);//ltm[i] 1-i中 串的最大值
         for(i=n-1;i>=1;i--)rtm[i]=max(rtm[i+1],rt[i]);//rtm[i] i-n中 串的最大值
         for(i=2;i<=n;i++)ans=max(ans,ltm[i-1]+rtm[i]);//ltm[i-1]+rtm[i] 1-(i-1) 与 i-n 两个串的和的最大值
         printf("%d\n",ans);
     }
     return 0;
 }

信息学奥赛一本通（C++版） 第二部分 基础算法 第九章 动态规划

你可能感兴趣的:(信息学奥赛一本通（C++版）)

信息学奥赛一本通（C++版）第二部分基础算法第九章动态规划