[十六]基础类型BigInteger简介
BigInteger和BigDecimal都是Java针对大数提供的类
超出了java的表示范围
属性简介
借助于signum和mag 来实现数据的符号位和实际数据的保存
final int signum 保存BigInteger的符号
| 负数 | -1 |
| 0 | 0 |
| 正数 | 1 |
final int[] mag;保存数字的数据
字节序为大端模式,大端模式就是低地址存储高位
数组的第一个元素必须是非0的,也就是如果有前导零将会被移除
这样可以保证每个数都有一个唯一的表示形式
这种要求下 BigInteger的0有一个0长度的数组保存
| 对于BigInteger 他的数据打开就是这么一种形式
[ 101....32位....1] [ 110....32个....1] ....N个..... [ 0110....32个....1]
它的真值的计算方法与其他的二进制序列一样的 二进制为 0111 1110 的十进制为126 相信谁都会计算,BigInteger也是如此的
尤其是对于BigInteger字符串参数的构造形式 千万不要以为就是把字符的编码或者字符转换成数字切段存放到int数组中 他存放的都是转换后的真值 下面会详细介绍 |
使用字节数组构造
内部是Int数组,一个int 32位就是 4个字节,所以自然是可以使用字节对BigInteger进行构造的
提供了两种形式的字节构造方法,可以指定符号的
使用字节进行构造,就是把所有的字节填充到int数组中
不过要注意的是,
计算机中存储的数值都是补码的形式
正数的补码与原码相同
负数的补码是他的原码取反再加一
就是把这些字节的补码按照顺序拼在一起,组合成int数组
- 如果是一个负数,会先得到真值的绝对值
- 如果有前导零,还会去掉所有的前导零
而且,是大端排序,大端排序,大端排序的把最终的数据存储起来
也就是说int数组中保存的都是真值的绝对值,使用专门的符号位记录正负和0
原码/反码/补码
先回顾下原码/反码/补码 的概念
| 原码 |
符号位+数值位 符号位为0 表示正数,符号位为1 表示负数
数值位就是真值的绝对值 又被称为带符号的绝对值表示 |
| 反码 | 正数的反码为其原码 负数的反码为其原码的除符号位外,逐位取反 |
| 补码 | 正数的补码为其原码 负数的补码为其反码+1 |
补码计算步骤
| 第一步求原码: 先写出来她的原码--->符号位+数值位(绝对值) |
| 第二步求反码: 如果是正数 反码与原码一样 如果是负数 反码为原码取反(除符号位外,逐位翻转) |
| 第三步求补码: 如果是正数 补码与原码一样 如果是负数 补码为反码 + 1 |
| 第四步扩充: 如果不足数据类型的宽度,将需要填充到指定宽度 符号位扩充,也就是正数补0 负数补1 |
| 总结 不管什么形式,第一位始终都是符号位,0 表示正数, 1表示负数 正数原码/反码/补码 全都一样,知道一种就直接得到另外的形式 负数如果知道补码,想要得到他的原码,只需要对补码再一次的求补码即可 |
示例1
示例2
通过这两个例子应该可以看得出来,数值都是补码形式存放
字节存储的也是补码 , int存储的也是补码,
所以使用字节构造 就是把所有的补码拼凑在一起就好了
拼凑排列好的补码,如果是正数,那么原码/反码/补码全都一样,存储的就是这个值
如果是负数,还需要取他的绝对值,绝对值就是 再求一次补码,去掉符号位就是绝对值了
BigInteger数组中,存储的都是真值的绝对值的补码,真值绝对值得补码,其实就是原码去掉符号位嘛,一个意思
就像上面的第二个例子 得到的补码为:
1000 0011 1111 0111 0000 0000 0101 1001
实际存储的是:
0111 1100 0000 1000 1111 1111 1010 0111
使用String构造
String作为参数的构造方法有两种形式
本质上只是一种,那就是指定基数的字符串转换为BigInteger
简化形式就是默认十进制的形式
通过String构造BigInteger的逻辑比较简单,但是实现看起来会有些令人模糊
接下来我们先介绍一点相关的计算基础
算法基础
int能够支撑的数据长度以及基数
我们知道,存储实际数据的是int数组
int表示范围是:
-231 ~ 231-1 也就是 -2147483648 ~ 2147483647
同理它内部也有两个针对Long 的数组,用于内部计算使用
| BigInteger内部使用int数组表示 普通数值使用每个数值位上的数字进行表示 |
| 一个BigInteger有多个int 一个普通数值有多个数字位 |
| 每个int能够表示的指定进制的最大值--intRadix 中保存的数据 其实 就是 BigInteger 的基于每个int作为一个元素的进制基数
|
说到这,我们再回头看看上面介绍的几个数组
| digitsPerInt 表示不同基数(进制)下一个int 能够表示的数字的长度 ,这个位数其实就是按照多长进行分割组装 intRadix 就是基数 bitsPerDigit 是用来推算需要多少个int的,也就是int数组的长度 |
以上是String构造BigInteger的用到的一些基本概念
构造方法源码解析
我们从构造方法入手,简单介绍下内部是如何运作的
public BigInteger(String val, int radix) {
//定义了两个变量一个光标,光标记录着应该要处理的数据索引下标
//另一个numDigits 用来保存需要处理的数字位数 也就是有效长度,比如去掉前导零后的
int cursor = 0, numDigits;
final int len = val.length();//传递进来的字符数组的长度
//如果给定的基数,不在合法范围内,那么抛出异常,不会默认处理
if (radix < Character.MIN_RADIX || radix > Character.MAX_RADIX)
throw new NumberFormatException("Radix out of range");
//如果字符串长度为0 也是一种非法的参数
if (len == 0)
throw new NumberFormatException("Zero length BigInteger");
// Check for at most one leading sign
int sign = 1;
int index1 = val.lastIndexOf('-');
int index2 = val.lastIndexOf('+');
//符号- + 只能出现一个,而且还必须是第一个位置,否则都不合法
//根据最后一个的索引与0 进行比较,可以简便的判断符号位是否合法
if (index1 >= 0) {
if (index1 != 0 || index2 >= 0) {
throw new NumberFormatException("Illegal embedded sign character");
}
sign = -1;
cursor = 1;
} else if (index2 >= 0) {
if (index2 != 0) {
throw new NumberFormatException("Illegal embedded sign character");
}
cursor = 1;
}
//经过前面的判断,如果有符号位的话,光标的值更新为1 也就是后续不处理符号位
//如果此时光标的值等于字符长度,说明没有有效数字了,将会抛出异常
if (cursor == len)
throw new NumberFormatException("Zero length BigInteger");
// Skip leading zeros and compute number of digits in magnitude
//如果有前导0 ,将会去掉这些,光标的位置也会跟着一起移动
while (cursor < len &&
Character.digit(val.charAt(cursor), radix) == 0) {
cursor++;
}
//跳过了所有的0之后就不再有有效数据了,说明他就是个0
//哪怕他原来设置的负数的0 将会变为0 的标记
if (cursor == len) {
signum = 0;
mag = ZERO.mag;
return;
}
//记录实际需要处理的数据长度以及对符号位使用signum进行记录
numDigits = len - cursor;
signum = sign;
// Pre-allocate array of expected size. May be too large but can
// never be too small. Typically exact.
//根据前面的公式计算实际需要的二进制位数 numDigits需要处理的数字的长度
//bitsPerDigit 里面记录了每个进制1位数需要的二进制位数,但是放大了1024倍,所以还要除以1024 也就是右移10
//真正的值可能是小数个,除以1024之后变成了取整了,然后再加上一,百分百够用,需要的比特位数保存到numBits
long numBits = ((numDigits * bitsPerDigit[radix]) >>> 10) + 1;
if (numBits + 31 >= (1L << 32)) {
reportOverflow();
}
//numWords 记录的是实际需要的int类型数据的个数,也就是数组的长度
//右移5位就是除以32 就是计算数组的长度,除法会取整,防止1个不足32位的时候,就会变成0了所以numBits加上31 之后再除以32
int numWords = (int) (numBits + 31) >>> 5;
//此时创建真正的保存数据的int数组了
int[] magnitude = new int[numWords];
// Process first (potentially short) digit group
//numDigits 需要处理的数字的个数
//digitsPerInt 保存的是每一个int能够保存的指定数制下的字符长度
//如果有余数,说明有一个不足最大长度的位数
//如果没有余数,那么每一组都是刚好能够保存的最大长度
int firstGroupLen = numDigits % digitsPerInt[radix];
if (firstGroupLen == 0)
firstGroupLen = digitsPerInt[radix];
//第一组数据存放到数组的最后一个
String group = val.substring(cursor, cursor += firstGroupLen);
magnitude[numWords - 1] = Integer.parseInt(group, radix);
if (magnitude[numWords - 1] < 0)
throw new NumberFormatException("Illegal digit");
// Process remaining digit groups
int superRadix = intRadix[radix];
int groupVal = 0;
while (cursor < len) {
group = val.substring(cursor, cursor += digitsPerInt[radix]);
groupVal = Integer.parseInt(group, radix);
if (groupVal < 0)
throw new NumberFormatException("Illegal digit");
// 这个方法是用来累计计算的,方法内部写的很复杂
//其实逻辑很简单,比如一个数字序列1234,求他表示的值是多少
// ( ( (1*10)+2 )*10+3 )*10 +4 = 1234
//这个方法就是用来计算的,只不过每一个位置是一个int 低32位当做数值 高32位当做进位
destructiveMulAdd(magnitude, superRadix, groupVal);
}
// Required for cases where the array was overallocated.
mag = trustedStripLeadingZeroInts(magnitude);
if (mag.length >= MAX_MAG_LENGTH) {
checkRange();
}
}
构造方法运行步骤
简单概括下这个方法:
前面的校验比较简单
1. 校验字符的合法性,并且获得符号位
2. 经过校验获取出来最终需要处理的字符的长度
然后就开始了计算
在正式计算之前,需要处理最高位,按照前面介绍的,能够表示的指定基数的最多位数进行划分
比如10进制表示9位,那么就是9个字符一组
先判断是否刚好整数倍?
如果不是,比如10位,那么这个最高位这一个数字自己一组,剩下的9位一组,将会被放到两个int中
获得了最高位之后,就开始正式进行计算
如果还有字符需要处理的话
1. 按照位数进行截取,比如10进制截取9位
2. 截取后转换为数值,然后destructiveMulAdd 这个方法就是第一个参数的数,乘以第二个参数,然后加上第三个参数
就是这样一个过程
( ( (1*10)+2 )*10+3 )*10 +4 = 1234
每一次的循环中int数组的值都会发生变化
最终获得最后的结果
字符串构造方法计算示例
使用字符串"-12345678986543215678901" 进行构造
我们按照方法的计算步骤走一下这个过程
看起来很繁琐复杂,好奇害死猫,分析这么多只是为了更好地了解这一过程
如果没兴趣只需要记住BigInteger可以直接把字符串转换为数值进行存储就好了
其他构造方法
另外还有两个构造方法
public BigInteger(int bitLength, int certainty, Random rnd)
构造一个随机生成的正 BigInteger,它可能是一个具有指定 bitLength 的素数
public BigInteger(int numBits, Random rnd)
构造一个随机生成的 BigInteger,它是在 0 到 (2numBits - 1)(包括)范围内均匀分布的值
方法简介
基础方法
| 获取符号位 signum() |
| 常用数学函数 negate() 取负 abs() 绝对值 pow(int) 求幂 gcd(BigInteger) 最大公约数 min(BigInteger) 最小值 max(BigInteger) 最大值 |
| 四则运算与取整求余 add(BigInteger) 加法 subtract(BigInteger) 减法 multiply(BigInteger) 乘法 divide(BigInteger) 除法(取整) remainder(BigInteger) 求余 divideAndRemainder(BigInteger) 取整和求余 返回的是一个数组 |
| 获取基本类型的值 不同于基本数值类型的包装类,此处并不是直接强转的 如果太大intValue 和 longValue 将分别返回低的32位和64位 longValue 和 doubleValue可能会被转换为无穷 intValue() longValue() floatValue() doubleValue() |
| 数值类型的准确值 longValueExact() intValueExact() shortValueExact() byteValueExact() 所谓准确就是不会舍入或者转换,因为他们会进行数据长度的校验 否则将会抛出异常 比如 |
| 位操作相关 and(BigInteger) 与 or(BigInteger) 或 not() 非 xor(BigInteger) 异或 andNot(BigInteger) 返回其值为 (this & ~val) 的 BigInteger 等效于 and(val.not()) shiftLeft(int) 左移 shiftRight(int) 右移 |
取模与求余对比
| 计算过程相同 对于整型数a,b来说,取模运算或者求余运算的方法都是:
求模运算和求余运算在第一步不同: 取余运算在取c的值时,向0 方向舍入; 而取模运算在计算c的值时,向负无穷方向舍入;
因此,求模时结果的符号与b一致,求余时结果的符号与a一致 如果a,b都是正整数的话,求模与求余没有区别 |
| mod(BigInteger) 返回其值为 (this mod m) 的 BigInteger,取模不同于 remainder
BigInteger modPow(BigInteger exponent,BigInteger m)
BigInteger modInverse(BigInteger m) |
bitCount与bitLength
| public int bitCount() 返回此 BigInteger 的二进制补码表示形式中与符号不同的位的数量 特别注意这个方法的含义 不是二进制补码表示形式的 1 位的数量,而是与符号不同的 |
| bitLength 最小的二进制补码表示形式的位数,不包括 符号位 对于正 BigInteger,这等于常规二进制表示形式中的位数 就是去掉符号位占用的长度 |
valueOf(long)
| valueOf(long) 包装一个long为BigInteger BigInteger的valueOf有缓冲的作用 |
![[十六]基础类型BigInteger简介_第22张图片](http://img.e-com-net.com/image/info8/c6b144c93c394278b10a5a6e26a0ee64.png) |
equals(Object)
| equals(Object) 重写了equals方法 数据相等 才是相等 |
![[十六]基础类型BigInteger简介_第23张图片](http://img.e-com-net.com/image/info8/0bf9dea7be434cc48f4ae488dd9f800e.png) |
toString hashCode CompareTo
| public String toString(int radix) 转换为指定基数 toString() |
| hashCode() |
| compareTo(BigInteger) 小于、等于或大于 时,返回 -1,0,或 1 |
素数相关
| 是否素数 public boolean isProbablePrime(int certainty) 如果此 BigInteger 可能为素数,则返回 true,如果它一定为合数,则返回 false 如果 certainty <= 0,则返回 true
参数: certainty - 调用方允许的不确定性的度量 如果该调用返回 true,则此 BigInteger 是素数的概率超出 ( 1 - 1/(2的certainty次方) ) 此方法的执行时间与此参数的值是成比例的 返回: 如果此 BigInteger 可能为素数,则返回 true,如果它一定为合数,则返回 false |
| public static BigInteger probablePrime(int bitLength, Random rnd) 返回有可能是素数的、具有指定长度的正 BigInteger此方法返回的 BigInteger 是合数的概率不超出 2的-100次方 参数: bitLength - 返回的 BigInteger 的 bitLength。 rnd - 随机比特源,用这些随机比特选择用来进行质数测试的候选数 |
| nextProbablePrime public BigInteger nextProbablePrime() 返回大于此 BigInteger 的可能为素数的第一个整数 此方法返回的数是合数的概率不超出 2的-100次方 |
特殊的"位操作"
| testBit(int) 计算 (this & (1< setBit(int) 计算 this | (1< clearBit(int) 计算 this & ~(1< flipBit(int) 计算 this ^ (1< |
| getLowestSetBit() 返回此 BigInteger 最右端(最低位)1 比特位的索引 也就是从最右边开始数找到的第一个1 此字节的右端开始到本字节中最右端 1 之间的 0 比特的位数 如果此 BigInteger 不包含1位,则返回 -1 计算 this==0? -1 : log2(this & -this) |
toByteArray
| public byte[] toByteArray() |
| BigInteger 内部使用int数组进行数据保存 一个int包含4个byte BigInteger可以使用byte数组构造 也自然能够分解成byte数组进行保存 |
总结
要记住,内部的存储int数组 是final int[] mag; 所以是不可变的
他只是用来表示超出Java范围内的数值
本身的方法虽然内部细节特殊
但是外部呈现并没有什么特别的,只不过不能使用平时的+-*/符号,需要使用专门的方法
它提供了BigInteger大数值作为数值的基本运算的对应方法
并且还提供了java.lang.Math 的所有相关方法
另外,BigInteger 还提供以下运算:模算术、GCD 计算、质数测试、素数生成、位操作以及一些其他操作
![[十六]基础类型BigInteger简介_第1张图片](http://img.e-com-net.com/image/info8/0fa1d0e187154495a848bfb98797f637.png)

![[十六]基础类型BigInteger简介_第2张图片](http://img.e-com-net.com/image/info8/b21010ac2b5f4721939fd816e72df1da.jpg)
![[十六]基础类型BigInteger简介_第3张图片](http://img.e-com-net.com/image/info8/7cd3486b7b9e4dbd9f8f544d22592709.png)
![[十六]基础类型BigInteger简介_第4张图片](http://img.e-com-net.com/image/info8/fd7f195f5aaf4f74a4f05b6ab4420f6e.png)
![[十六]基础类型BigInteger简介_第5张图片](http://img.e-com-net.com/image/info8/9760cb7ff93e47949901b6378c79b986.jpg)
![[十六]基础类型BigInteger简介_第6张图片](http://img.e-com-net.com/image/info8/7595cc854f8847699c68fac53f02ecbc.jpg)
![[十六]基础类型BigInteger简介_第7张图片](http://img.e-com-net.com/image/info8/93053f58ce67466890b22829469e3744.jpg)
![[十六]基础类型BigInteger简介_第8张图片](http://img.e-com-net.com/image/info8/b1490a2b33db42e09cd093b9f383c287.jpg)
![[十六]基础类型BigInteger简介_第9张图片](http://img.e-com-net.com/image/info8/7674d28199864bf0933344885693f5ed.jpg)
![[十六]基础类型BigInteger简介_第10张图片](http://img.e-com-net.com/image/info8/458fbba39397445bbedb71d9bbe74b30.png)
![[十六]基础类型BigInteger简介_第11张图片](http://img.e-com-net.com/image/info8/2c71741fb08a4ec8ac9582973cad1c69.png)
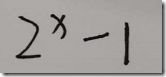
![[十六]基础类型BigInteger简介_第12张图片](http://img.e-com-net.com/image/info8/e22e983644e74f16bf693198a2a66bb5.jpg)
![[十六]基础类型BigInteger简介_第13张图片](http://img.e-com-net.com/image/info8/499d4ec6a19b4e2a90c48b6626e521fe.jpg)
![[十六]基础类型BigInteger简介_第14张图片](http://img.e-com-net.com/image/info8/d56fa01c99cf4269bb16aab9108f8a44.jpg)
![[十六]基础类型BigInteger简介_第15张图片](http://img.e-com-net.com/image/info8/d3f885487d4240b2ada3e5a8d59fcf19.png)
![[十六]基础类型BigInteger简介_第16张图片](http://img.e-com-net.com/image/info8/3b062cef14d3405a90b70d2d9ea3792e.png)
![[十六]基础类型BigInteger简介_第17张图片](http://img.e-com-net.com/image/info8/9cb68e645ed446698ad6520c8f6d0dec.png)
![[十六]基础类型BigInteger简介_第18张图片](http://img.e-com-net.com/image/info8/2b9e176061424fcf8f7e0d299caaa6bf.png)

![[十六]基础类型BigInteger简介_第19张图片](http://img.e-com-net.com/image/info8/fcc4fed918164bb3880eacf7078ec9fa.png)
![[十六]基础类型BigInteger简介_第20张图片](http://img.e-com-net.com/image/info8/185e92596ba94826b8cd6e1514aa649f.png)
![[十六]基础类型BigInteger简介_第21张图片](http://img.e-com-net.com/image/info8/ff44abee978f4208b5e48e4d846afdfc.png)

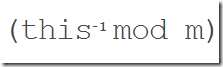
![[十六]基础类型BigInteger简介_第24张图片](http://img.e-com-net.com/image/info8/454dd5a7987e45aa9c793a8a9f62e712.jpg)