从九宫问题浅谈广度优先搜索与深度优先搜索策略

九宫拼图游戏

先说说一个游戏，大多数80后、90后小时候应该都玩过一个拼图游戏，一共9个格子，其中一个是空的格子，剩下8个是被打乱的图片残块，通过移动图片残块来复原最初的图像，这个游戏就是九宫拼图游戏。进阶的还有4乘4，16宫格的，呃，扯远了。

状态、结点与路径

那么对于这个游戏，我们尝试用状态去描述它，那么它的复原过程就是一个个状态的组合，或者说是排列。它有一个初始状态，有一个目标状态，还有若干个不确定的中间状态。我们要从初始状态变换到目标状态，中间就会产生一些中间状态，连起来就是一条条的路径，可能这条路径行不通，就需要换另一条路径。路径上的各个状态也称为结点。

九宫问题

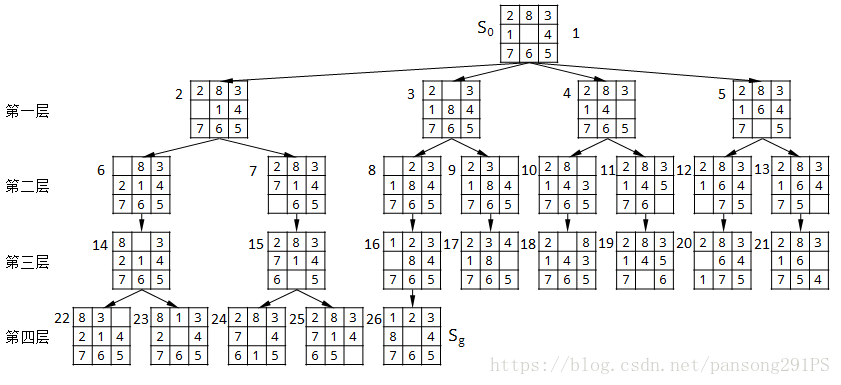
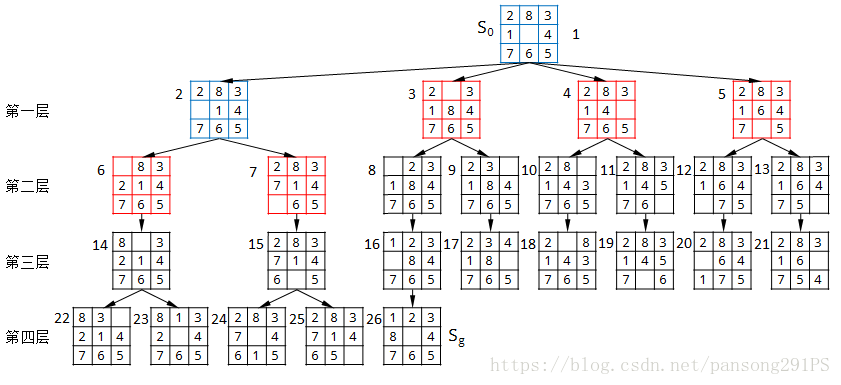
那么现在有一个九宫格，初始状态为S0，目标状态为Sg，只允许把位于空格上下左右的数字块移入空格，要求寻找从初始状态到目标状态的路径。

这里不妨做一个移动对象的转换，把数字块的移动看成是空格块的移动，那么在初始状态S0中，数字块8下移就变成了空格块上移，这样的好处就是方便描述和理解，当我们获取S0的次态（下一个可能的状态）时，就不是数字块8的下移、数字块6的上移、数字块1的右移和数字块4的左移，而是空格块的上下左右移动了。

状态空间的一般搜索过程

问题求解过程实际上是一个搜索过程。通过运用搜索技术解决此问题的基本思想是，首先把问题的初始状态（即初始结点）作为当前状态，适当的对其进行运算操作，生成一组子状态（或后继状态、后继结点、子结点），然后检查目标状态是否在其中出观。若出现，则搜索成功，找到了问题的解；若不出现，则按某种搜索策略从已生成的状态中再选一个状态作为当前状态，重复上述过程，直到目标状态出现或者不再有可供运算操作的状态时为止。

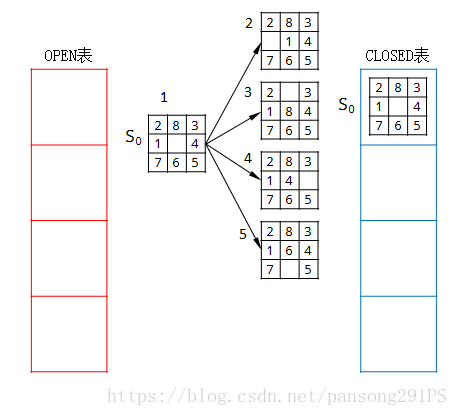
在搜索过程中，要建立两个数据结构：OPEN表和CLOSED表，其形式分别如图所示。

OPEN表用于存放刚生成的、还未扩展的结点，对不同的策略，结点在此表中的排列顺序是不同的。例如对广度优先搜索，是将扩展结点n的子结点放入到OPEN表的尾部，而深度优先搜索，则是把结点的子结点放入到OPEN表的首部。

CLOSED表用于存放已扩展的结点。所谓对一个结点进行扩展，是指用合适的算法对该结点进行运算操作，生成一组子结点。需要注意的是，在这些子结点中，可能有些是当前扩展结点（即结点n）的父结点、祖父结点等。此时不能把这些先辈结点作为当前扩展结点的子结点，否则会出现无限重复死循环。

搜索的一般过程如下：

（1）把初始结点S0放入OPEN表中。

（2）检查OPEN表是否为空，若为空则问题无解，退出。否则进行下一步。

（3）把OPEN表的第一个结点取出放入CLOSED表中。并记该结点为结点n。

（4）考虑结点n是否为目标结点，若是，则求得问题的解，退出。此解可从目标结点开始直到初始结点的返回指针中得到。否则，继续下一步。

（5）扩展结点n，若没有后继结点，则立即转步骤（2），否则生成一组子结点，把其中是结点n的先辈的子结点去掉。

（6）针对子结点的不同情况，分别进行如下处理：

①对于那些未曾在CLOSED表中出现过的子结点，设置一个指向父结点（即结点n）的指针，并把它们放入OPEN表中。

②对于那些先前已在CLOSED表中出现过的子结点，确定是否需要修改它指向父结点的指针。

（7）按某种搜索策略对OPEN表中的结点进行排序。

（8）返回至第（2）步。

下面对上述过程作一些必要的说明。

（1）上述过程是状态空间的一般搜索过程，具有通用性，在此之后讨论的各种搜索策略都可看做是它的一个特例。各种搜索策略的主要区别是对OPEN表中结点排序的准则不同。

（2）不能把当前结点的先辈作为当前结点的子结点。

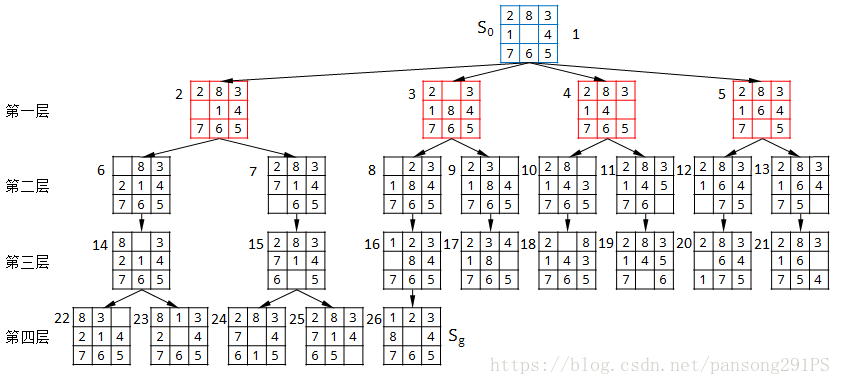
（3）新生成的结点，有可能是之前已经生成过的结点，此时，就可能出现一个子结点有多个父结点的情况，应选取其中一个父结点，使得该结点到原始结点的路径最短，即代价最小。现举例说明，设下图第一张为搜索过程所形成的图，其中实心黑点代表已扩展了的结点，它们位于CLOSED表上；空心圆圈代表未扩展的结点，它们位于OPEN表上，有向箭头是指向父结点的指针，它们是在步骤（6）形成的，例如结点3是结点2的父结点。

假设现在要扩展结点1，并且只生成单一的子结点2。但是目前结点2已有父结点3，那结点2在先前扩展结点3时已被生成了，现在又作为结点1的子结点被再次生成。此时，为确定哪一个结点作为结点2的父结点，需要计算路径代价。假设每条边的代价为1，则从S0经右边路径到结点2的代价为2，而从S0经中间路径到结点2的代价为4，显然右边路径到结点2的代价较小，因此应修改结点2指向父结点的指针，让它指向结点1，即把结点1作为结点2的父结点，不再以结点3作为它的父结点。另外，结点4既然是结点2的子结点又是结点5的子结点，当结点2以结点3作为父结点时，由于从S0经中间路径到结点4的代价大于从S0经左边路径到结点4的代价，所以结点4以结点5为父结点。但是，经扩展结点1之后，从S0经右边路径到结点4的代价为3，而从S0经左边路径到结点4的代价为4，所以结点4不能再以结点5为父结点，而需要改为以结点2为父结点。此时，搜索图如上图第二张所示。这就是搜索过程步骤（6）所阅述的内容。

广度优先搜索策略

广度优先搜索（也称宽度优先搜索）的基本思想是：从初始结点S0开始，逐层地对结点进行扩展并考察它是否为目标结点，在第n层的结点没有全部扩展并考察完之前，不对第n+1层的结点进行扩展。OPEN表中的结点总是按照进入的先后顺序排列，先进入的结点排在前面，后进入的排在后面。其搜索过程只需将一般搜索过程中的第（7）步改为始终将新生成的节点放入OPEN表的尾部即可。下面根据九宫问题给出广度优先搜索的详细图解。

先看如下树状图。

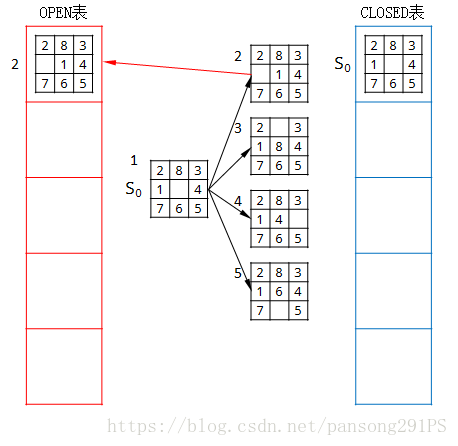
1、搜索开始，先把S0放入OPEN表。

2、判断OPEN表是否为空，不是则继续，如下图。

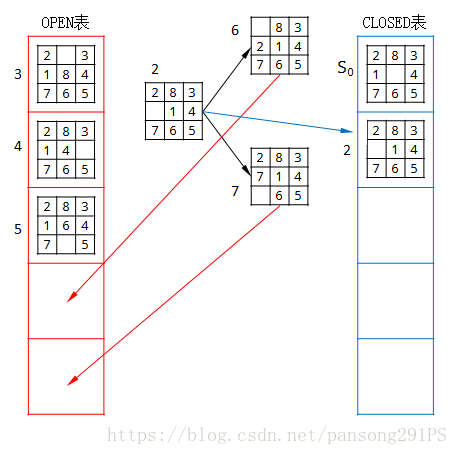
3、将OPEN表第一个结点取出并放入CLOSED表中，判断是否为目标结点，若不是求得该结点的所有可能子结点，如下图。

4、将其中是结点n的先辈的子结点去掉，剩余的放入OPEN表的尾部，如下图。

此时对应的树状图如下。

5、重复2、3、4，判断OPEN表，不为空，继续将OPEN表第一个结点取出并放入CLOSED表中，判断是否为目标结点，若不是求得该结点的所有可能子结点，将其中是结点n的先辈的子结点去掉（这里去掉了一个空格块右移的情况，因为这个情况就是结点2的先辈，也就是结点S0），剩余的放入OPEN表的尾部，如下图。

此时对应的树状图如下。

6、继续重复，可以得到以下各图。

可以看出，从初始结点S0开始，逐层地对结点进行扩展并考察它是否为目标结点，在第n层的结点没有全部扩展并考察完之前，不对第n+1层的结点进行扩展。而OPEN表中的结点总是按照进入的先后顺序排列，先进入的结点排在前面，后进入的排在后面。

综上，广度优先搜索就是横向搜索，直到找到目标结点或者全部搜索完毕。第3步的判断当前结点是否是目标结点，如果是则找到了路径。而第2步的判断则是判断是否全部搜索完毕，如果全部搜索完了的话，最后一个结点是不能扩展子结点的，或者说扩展出来的子结点全部都是先辈结点，全部都被去掉了，最后OPEN表自然就是空的。

由此，可以得出九宫问题的解了，解得路径是S0→3→8→16→26。由于广度优先搜索总是在扩展完n层的结点之后才转向n+1层，所以它总能找到路径最优解（花费的层数最少），但实用意义不大，因为每层搜索生成的后裔较大，最后导致组合爆炸，尽管资源耗尽，也可能会在可利用的空间中找不到解。

深度优先搜索策略

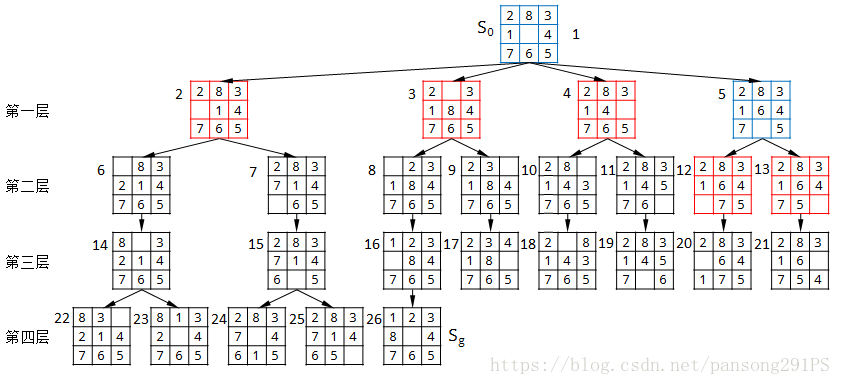
深度优先搜索的基本思想是：从初始结点S0开始扩展，若没有得到目标结点，则选择最后产生的子结点进行扩展，若还是不能到达目标结点，则再对刚才最后产生的子结点进行扩展，一直如此向下搜索。当到达某个子结点，且该子结点既不是目标结点又不能继续扩展时，才选择其兄弟结点进行考察。其搜索过程只需将一般搜索过程中的第（7）步改为始终将新生成的节点放入OPEN表的首部即可。下面根据九宫问题给出深度优先搜索的详细图解。

1、搜索开始，前几步是一样的。

2、将其中是结点n的先辈的子结点去掉，剩余的放入OPEN表的首部（只有这里不一样，是放至表首），这里为了更加清晰地展示这个过程，拆解成了多张图片。

每一次放入结点时，都是放在OPEN表的表首。可以看出，结点在OPEN表中的排序规则与广度优先是不一样的，此时对应的树状图如下。

树状图貌似与广度优先的一样，实际上这里深度优先的树状图的第一层顺序是从右至左的。

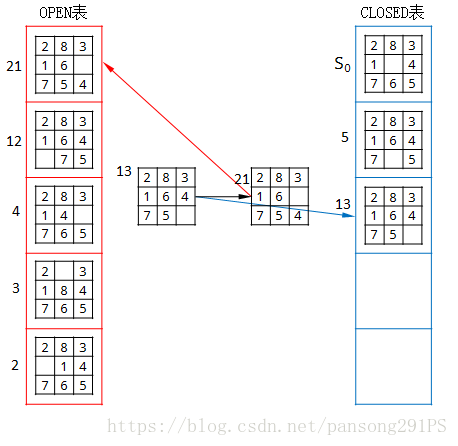
3、继续重复，判断OPEN表，不为空，继续将OPEN表第一个结点取出并放入CLOSED表中，判断是否为目标结点，若不是求得该结点的所有可能子结点，将其中是结点n的先辈的子结点去掉（这里去掉了一个空格块上移的情况，因为这个情况就是结点5的先辈，也就是结点S0），剩余的放入OPEN表的首部，如下图。

注意结点12和结点13放入OPEN表的位置，先把结点12放入OPEN表的表首，再把结点13放入OPEN表的表首。每一次放入结点时，都是放在OPEN表的表首。如果你把结点12和结点13一起放入表首，OPEN表的顺序就变成12，13，4，3，2了，这样是不正确的。正确的深度优先搜索，OPEN表的顺序一定是倒序的。此时对应的树状图如下。

4、继续重复，可以得到以下各图。

可以看出，深度优先搜索就是纵向搜索，搜索一旦进入某个分支，就将沿着该分支一直向下搜索。若目标结点恰好在此分支上，则可较快得到解。但是，若目标结点不在此分支上，而该分支又是一个无穷分支，则就不可能得到解。所以深度优先搜索是不完备的，即使问题有解，它也不一定能求得到解。且用深度优先搜索求得的解，不一定是路径最优的解。OPEN表中的结点排列总是，先进入的结点排在后面，后进入的排在前面。

盲目搜索与启发式搜索策略

一、有界深度优先搜索

为了解决深度优先搜索不完备问题，避免搜索过程陷入无穷分支的死循环，提出了有界深度优先搜索方法。有界深度优先搜索的基本思想是：对深度优先搜索方法引入搜索深度的界限，当搜索深度达到了深度界线，而尚未出现目标结点时，就换一个分支进行搜索。

二、代价树的广度优先搜索和代价树的深度优先搜索

上面讨论的广度优先搜索和深度优先搜索都没有考虑搜索代价问题，而只假设各边的代价均相同，且为一个单位量，实际上，各边的代价不会相同，故在搜索过程中还应对此进行考虑，这类搜索称之为代价树的广度优先搜索和代价树的深度优先搜索。

以上五种搜索策略都是盲目搜索。它们的一个共同特点就是它们的搜索路线是事先决定好的，是按照固定的顺序去进行搜索的，因而这样的搜索策略都具有较大的盲目性。盲目搜索所需扩展的结点数目很大，产生的无用结点肯定就很多，效率就会较低。

三、启发式搜索

盲目搜索没有利用被求解问题的任何特征信息，在决定要被扩展的结点时，没有考虑该结点到底是否可能出现在解的路径上，也没有考虑它是否有利于问题的求解以及所求得的解是否为最优解（广度优先搜索能得到路径最优解，但不一定能得到代价最优解）。若能找到一种搜索方法，能充分利用待求解问题自身的某些特性信息，以指导搜索朝着最有利于问题求解的方向发展，即在选择结点进行扩展时，优先选择那些最有希望的结点加以扩展，则搜索效率就会大大提高。这种利用问题自身特性信息，以提高搜索效率的搜索策略，称为启发式搜索。关于更详细的介绍，请查阅相关文献资料。

参考资料

《人工智能技术》曹承志主编，清华大学出版社