洛谷 P1514 引水入城 ( 记忆化搜索+贪心） 题解

题目来源：

https://www.luogu.org/problemnew/show/P1514

题目描述：

题目描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个NN 行\times M×M 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第11 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第NN 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入输出格式

输入格式：

 

每行两个数，之间用一个空格隔开。输入的第一行是两个正整数N,MN,M，表示矩形的规模。接下来NN 行，每行MM个正整数，依次代表每座城市的海拔高度。

 

输出格式：

 

两行。如果能满足要求，输出的第一行是整数11，第二行是一个整数，代表最少建造几个蓄水厂；如果不能满足要求，输出的第一行是整数00，第二行是一个整数，代表有几座干旱区中的城市不可能建有水利设施。

 

输入输出样例

输入样例#1： 复制

2 5
9 1 5 4 3
8 7 6 1 2

输出样例#1： 复制

1
1

输入样例#2： 复制

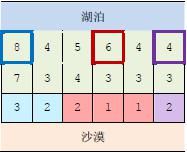
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2

输出样例#2： 复制

1
3

说明

【样例1 说明】

只需要在海拔为99 的那座城市中建造蓄水厂，即可满足要求。

【样例2 说明】

上图中，在33个粗线框出的城市中建造蓄水厂，可以满足要求。以这33个蓄水厂为源头在干旱区中建造的输水站分别用3 种颜色标出。当然，建造方法可能不唯一。

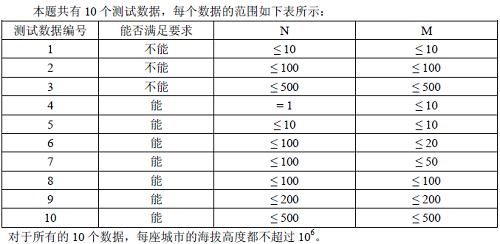
【数据范围】

解题思路：

        我们可以知道，每一个点能到的沙漠区都是连续的，我们只要求出左端点和右端点就行，我们用dp的思想，l【x】【y】=min（l【nx】【ny】），nx，ny是x，y能到的点，r【x】【y】同理，用记忆化dfs搜索，求出所有的湖泊区的点能到的区间，我们还要用一个vis数组记录每个点的到达情况，然后就可以判断是否可以覆盖所有沙漠城市。

我们关键是求最少用几个城市覆盖多有沙漠的问题，这时候问题变成了，n条线段，问覆盖一个区间最少要几条，我们可以贪心的去做，就是按照左端点从小到大排序，然后再找一条左端点比上一条右端点小或等的，且右端点最大的，依次找下去直到覆盖整个区间。。。。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include