赫夫曼数——文件压缩与解压
一、赫夫曼树
1.概念
赫夫曼树:给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称为赫夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。
-
赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
-
路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1
-
结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积
-
树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
2.创建一颗赫夫曼树
步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗赫夫曼树
以{13,7,8,3,29,6,1}为例,图解:
首先进行排序得到{1,3,6,7,8,13,29}
然后构建赫夫曼树:

取出最小的和次小的1和3,构建出一颗新的二叉树,然后得到新的{4,6,7,8,13,29}
接下来再取出最小的和次小的4和6,构建出一颗新的二叉树

依次这样。。。。之后得到赫夫曼数:
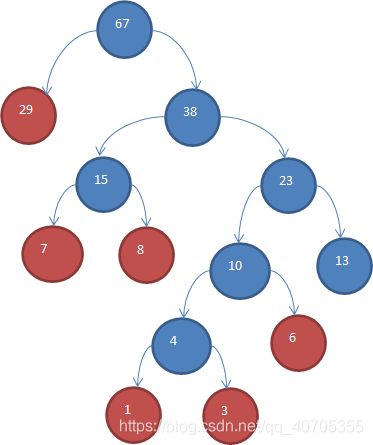
红色标记的为原数组的内容。
代码实现:
节点信息
public class Node implements Comparable {
private int value;
private Node left; // 左子节点
private Node right;// 右子节点
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
// 前序遍历
public void preOrder(Node node){
System.out.println("node => " + node);
if (node.getLeft() != null){
preOrder(node.getLeft());
}
if (node.getRight() != null){
preOrder(node.getRight());
}
}
@Override
public int compareTo(Object o) {
return this.getValue() - ((Node)o).getValue();
}
}
创建一颗赫夫曼树
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node huffmanTree = createHuffmanTree(arr);
HuffmanTree huffmanTree1 = new HuffmanTree();
huffmanTree1.preOrder(huffmanTree);
}
public void preOrder(Node huffmanTree){
if (huffmanTree != null){
huffmanTree.preOrder(huffmanTree);
}
}
/**
* @Description: createHuffmanTree 创建一个赫夫曼数
* @param: [arr ]
* @return: tree.huffmanTree.Node
* @auther: zqq
* @date: 20/6/21 17:04
*/
public static Node createHuffmanTree(int[] arr){
ArrayList<Node> nodes = new ArrayList<>();
for (int item : arr) { // 将数组内的数据加入链表
nodes.add(new Node(item));
}
while (nodes.size() > 1){ // 知道只有一个节点为止
Collections.sort(nodes);
// 1. 取出第一个数(最小的)
Node leftNode = nodes.get(0);
// 2. 取出第二个数(次小的)
Node rightNode = nodes.get(1);
// 3. 创建父node
Node parentNode = new Node(leftNode.getValue() + rightNode.getValue());
parentNode.setLeft(leftNode);
parentNode.setRight(rightNode);
// 4. 从ArrayList 删除处理过的二叉树
nodes.remove(leftNode); // 删除最小的
nodes.remove(rightNode); // 删除次小的
// 5. 将 parent 加入到 nodes
nodes.add(parentNode);
}
return nodes.get(0);
}
}
二、赫夫曼编码
1.介绍
-
赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法
-
赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
-
赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%~90%之间
-
赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,称之为最佳编码
2.通信编码处理方式
1).定长编码
如:
i like like like java do you like a java
对应的ASCII码为:
105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97
对应的二进制数为:
01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001
很长。
2).变长编码
还是对上面的字符,进行字符统计:
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数
对统计结果进行编码
0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d 按照各个字符出现的次数进行编码,原则是出现次数越多的,则编码越小,比如 空格出现了9 次, 编码为0 ,其它依次类推.
按照上面给各个字符规定的编码,则我们在传输 “i like like like java do you like a java” 数据时,编码就是
![]()
这里要介绍一个概念:前缀编码
前缀编码: 字符的编码都不能是其他字符编码的前缀,符合此要求的编码叫做前缀编码, 即不能匹配到重复的编码
显然上面的编码是方式是不符合前缀编码的,会导致解码的时候不知道解码是的那个字符:如10对应的i和100对应的k,当遇见100时是解码成为i 还是解码成为k
3.赫夫曼编码
像变长编码一样统计字符出现的次数,次数作为赫夫曼树的权值,进行构建赫夫曼树。如图:

根据赫夫曼树,给各个字符,规定编码 (前缀编码), 向左的路径为0 向右的路径为1 , 编码如下:
o: 1000, u: 10010, d: 100110 , y: 100111, i: 101, a : 110 , k: 1110, e: 1111 , j: 0000, v: 0001 , l: 001 , : 01
赫夫曼数满足前缀编码。
按照上面的赫夫曼编码,我们的"i like like like java do you like a java" 字符串对应的编码为 (使用的无损压缩)
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
长度为 : 133
说明:
- 原来长度是 359 , 压缩了 (359-133) / 359 = 62.9%
- 此编码满足前缀编码, 即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性
是不是长度少了很多尼,但是若是以这个来进行传输就比原来的字符长度还要长了,所以这里我们还需要将其以8个为一组转换为对应的字符。
赫夫曼树根据排序不同得到的赫夫曼编码不一样,但是WPL是一样的,都是最小的。
3.赫夫曼树对字符串压缩
首先要得到字符串对应的字节数组:
String str = "i like like like java do you like a java";
byte[] bytes = str.getBytes();
将字符串对应的字节数组转换为包含节点信息的list:
/**
* @Description: getNodes 将字节数字转换为包含Node节点的List
* 如:[Node[data = 97, weight = 5],...]
* @param: [bytes]
* @return: java.util.List
* @auther: zqq
* @date: 20/6/23 14:56
*/
public static List<Node> getNodes(byte[] bytes){
List<Node> nodes = new ArrayList<>();
HashMap<Byte, Integer> stringHashMap = new HashMap<Byte, Integer>();
// 同记每一只字母出现的次数
for (byte aByte : bytes) {
if (!stringHashMap.containsKey(aByte)){
stringHashMap.put(aByte,1);
}else {
stringHashMap.replace(aByte,stringHashMap.get(aByte) + 1);
}
}
// 将map的内容转换到list中
for (Map.Entry<Byte, Integer> byteIntegerEntry : stringHashMap.entrySet()) {
nodes.add(new Node(byteIntegerEntry.getKey(), byteIntegerEntry.getValue()));
}
return nodes;
}
根据上述的list生成赫夫曼树:
/**
* @Description: createHuffmanTree 将包含节点的nodes转换成为赫夫曼树
* @param: [nodes]
* @return: huffmancode.Node
* @auther: zqq
* @date: 20/6/23 15:10
*/
public static Node createHuffmanTree(List<Node> nodes){
while (nodes.size() > 1){
Collections.sort(nodes); // 1 排序
Node first = nodes.get(0);// 2.找出最小和次小节点
Node second = nodes.get(1);
Node parent = new Node(null, first.getWeight() + second.getWeight()); // 3.创建它们的父节点
parent.setLeft(first); // 4.将父节点与子节点形成关系
parent.setRight(second);
nodes.remove(first); //5. 删除建立好关系的节点
nodes.remove(second);
nodes.add(parent); // 将新的节点加入list
}
return nodes.get(0);
}
根据赫夫曼树创建赫夫曼表:
/**
* @Description: getCodes 得到node所有子节点节点的赫夫曼编码,并放入huffmanCodes集合中
* @param: [node, code: 左子节点是0,右子节点是1, stringBuilder:拼接路径]
* @return: void
* @auther: zqq
* @date: 20/6/23 15:40
*/
public static void getCodes(Node node, String code, StringBuilder stringBuilder){
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
stringBuilder2.append(code);
if (node.getData() == null){ // 不是叶子节点
getCodes(node.getLeft(), "0",stringBuilder2);
getCodes(node.getRight(), "1",stringBuilder2);
}else { // 是叶子节点
huffmanCodes.put(node.getData(), stringBuilder2.toString());
}
}
/**
* @Description: getCodes 重载方法
* @param: [node]
* @return: void
* @auther: zqq
* @date: 20/6/23 15:47
*/
public static Map<Byte, String> getCodes(Node node){
if (node == null){
return null;
}
// 处理左子树
getCodes(node.getLeft(), "0", stringBuilder);
// 处理右子树
getCodes(node.getRight(), "1", stringBuilder);
return huffmanCodes;
}
再根据字符串对应的自己数组与赫夫曼表进行压缩:
/**
* @Description: zip 将字符串对应的byte[] 数组,通过生成的赫夫曼编码表,,返回一个赫夫曼压缩后的byte[]
* @param: [bytes, huffmanCodes]
* @return: byte[]
* @auther: zqq
* @date: 20/6/23 16:39
*/
public static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes){
StringBuilder stringBuilder = new StringBuilder();
for (byte aByte : bytes) { //
stringBuilder.append(huffmanCodes.get(aByte));
}
int len = (stringBuilder.length() + 7) / 8;// 计数字节数组的长度
// 创建存储压缩后的byte数组
byte[] huffmanCodeBytes = new byte[len];
int index = 0;
String stringByte;
for (int i = 0; i < stringBuilder.length(); i+= 8 ) {
if (i + 8 > stringBuilder.length() ){
stringByte = stringBuilder.substring(i);
}else {
stringByte = stringBuilder.substring(i, i + 8);
}
// 将stringByte转换为一个byte,存放到huffmanCodeBytes
huffmanCodeBytes[index++] = (byte) Integer.parseInt(stringByte,2);
}
return huffmanCodeBytes;
}
这样就得到了压缩后的字节数组。
4.对字符串进行解压
根据哈夫曼表与压缩后的字节数组逆向一次就可以得到原字符串
/**
* @Description: decode 将字节数组转换为字符转换的字节数组
* @param: [huffmanCodes 赫夫曼编码表, huffmanBytes 赫夫曼编码得到的字节数组]
* @return: byte[]
* @auther: zqq
* @date: 20/6/23 18:03
*/
public static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes){
// 1.先得到huffmanBytes对应的二进制字符串
StringBuilder stringBuilder = new StringBuilder();
// 2.将byte字节数组转换为二进制的字符串
for (int i = 0; i < huffmanBytes.length; i++) {
// 判断是不是最后一个字节
boolean flag = (i == huffmanBytes.length-1); // 不足需要补位的标志
stringBuilder.append(byteToBitString(!flag, huffmanBytes[i]));
}
HashMap<String, Byte> map = new HashMap<>();
// 将赫夫曼编码进行调换,需要进行方向查询
for (Map.Entry<Byte, String> byteStringEntry : huffmanCodes.entrySet()) {
map.put(byteStringEntry.getValue(), byteStringEntry.getKey());
}
ArrayList<Byte> list = new ArrayList<>();
for (int i = 0; i < stringBuilder.length();) {
int count = 1;
Boolean flag = true;
Byte b = null;
while (flag){
String key = stringBuilder.substring(i, i + count);// count移动匹配一个字符
b = map.get(key);
if (b == null){
count++;
}else {
flag = false;
}
}
list.add(b);
i += count;
}
// for循环结束后,list中就存放了所有字符
// 把list中的数据放入到byte[]中,并返回
byte[] b = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
/**
* @Description: byteToBitString 将一个byte转成一个二进制字符串
* @param: [flag 标志是否需要补高位,true表示补齐高位, b]
* @return: java.lang.String 二进制对应的字符串
* @auther: zqq
* @date: 20/6/23 17:50
*/
public static String byteToBitString(boolean flag, byte b){
int temp = b;
// 如果是正数,需要补高位
if (flag){
temp |= 256;
}
String str = Integer.toBinaryString(temp); // 返回的是二进制对应的补码
if (flag){
return str.substring(str.length() - 8);
}else {
return str;
}
}
三、对文件的压缩与解压
1.文件压缩
原理与字符串一样,只是引入了IO流:
/**
* @Description: zipFile 对文件进行压缩
* @param: [srcFile, dstFile]
* @return: void
* @auther: zqq
* @date: 20/6/23 21:59
*/
public static void zipFile(String srcFile, String dstFile){
FileInputStream is = null;
FileOutputStream os = null;
ObjectOutputStream oos = null;
try{
is = new FileInputStream(srcFile);
// 创建一个和源文件大小一样的byte[]
byte[] b = new byte[is.available()];
is.read(b);//读取文件
// 对文件进行压缩
byte[] bytesCode = HuffmanCode.huffmanZip(b);
//创建文件输出流
os = new FileOutputStream(dstFile);
//创建一个和文件输出流关联的流objectOutputStream
oos = new ObjectOutputStream(os);
// 将压缩好后的字节数组写输入输出流
oos.writeObject(bytesCode);
// 将赫夫曼编码表写如,才可以解压
oos.writeObject(huffmanCodes);
}catch (Exception e){
System.out.println("e.getMessage() = " + e.getMessage());
}finally {
try {
is.close();
os.close();
oos.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
2 .对文件解压
/**
* @Description: unZip 解压文件
* @param: [srcFile, dstString]
* @return: void
* @auther: zqq
* @date: 20/6/23 22:09
*/
public static void unZipFile(String srcFile, String dstString){
FileInputStream is = null;
ObjectInputStream ois = null;
FileOutputStream os = null;
try {
is = new FileInputStream(srcFile);
ois = new ObjectInputStream(is);
// 读取赫夫曼编码
byte[] huffmanBytes = (byte[]) ois.readObject();
// 读取赫夫曼编码表
Map<Byte, String> huffmanCodes = (Map<Byte, String>) ois.readObject();
byte[] bytes = decode(huffmanCodes, huffmanBytes);
os = new FileOutputStream(dstString);
os.write(bytes);
}catch (Exception e){
e.printStackTrace();
}finally {
try {
is.close();
ois.close();
os.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
}
全部代码参考供下载
四、注意事项
- 如果文件本身就是经过压缩处理的,那么使用赫夫曼编码再压缩效率不会有明显变化, 比如视频,ppt 等等文件
- 赫夫曼编码是按字节来处理的,因此可以处理所有的文件(二进制文件、文本文件)
- 如果一个文件中的内容,重复的数据不多,压缩效果也不会很明显.
