dfs详解————by ly，cx
• DFS:
• 全名:Depth-First-Search,中文名:深度优先搜索。
• 算法简要过程:对每一个可能的分支路径深入到不能再深入为止,而且每个节
点只能访问一次。以上均为百度百科以及强大怪的的che dan
首先先讲思想（口胡）
图的dfs
当然树形结构也一样。
简单的就不说了，给出一种模板
void dfs(答案,搜索层数,其他参数){
if(层数==maxdeep){
更新答案;
return;
}
(剪枝)
for(枚举下一层可能的状态){
更新全局变量表示状态的变量;
dfs(答案+新状态增加的价值,层数+1,其他参数);
还原全局变量表示状态的变量;
}
}进入正题，简单的dfs没什么好讲的，我们来讲讲dfs的奇淫巧技
1.dfs遍历图
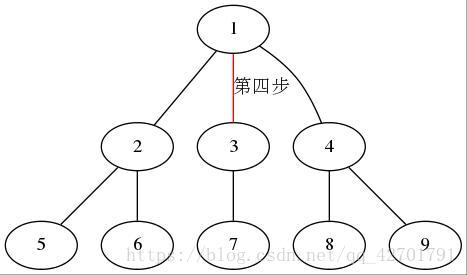
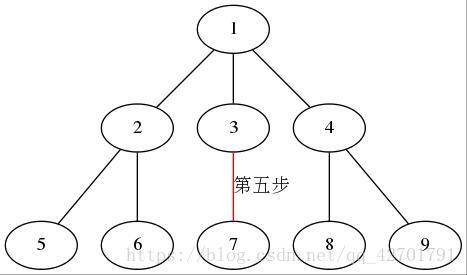
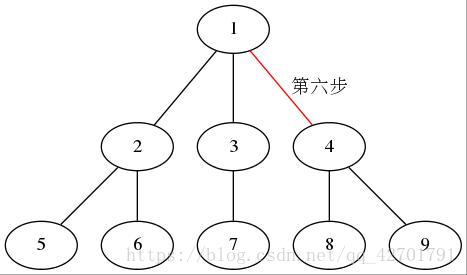
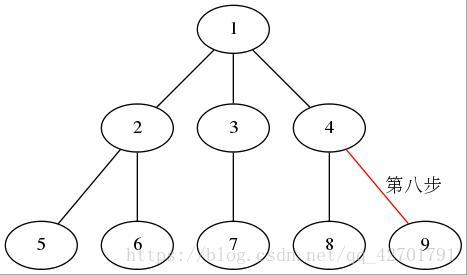
之前的图大家也看了，我们发现dfs可以遍历一张图
从图中某个顶点v出发，首先访问v;访问结点v的第一个邻接点，以这个邻接点vt作为一个新节点，访问vt所有邻接点。直到以vt出发的所有节点都被访问到，回溯到v的下一个未被访问过的邻接点，以这个邻结点为新节点，重复上述步骤，直到图中所有与v相通的所有节点都被访问到。若此时图中仍有未被访问的结点，则另选图中的一个未被访问的顶点作为起始点。重复该过程，直到图中的所有节点均被访问过。
用一个b数组记录该点是否被访问过。
#include
#include
#include
#include
using namespace std;
struct Edge
{
int to,w,next;
}edge[100001];
int k,n,m,x,y,z,sum=0,b[100001],head[100001];
inline void add(int u,int v,int w)//领接链表建图
{
edge[++k].to=v;
edge[k].w=w;
edge[k].next=head[u];
head[u]=k;
}
void dfs(int u)//dfs遍历,u表示当前所在的起点编号
{
sum++;
if(sum==n)return;
for(register int i=head[u];i;i=edge[i].next)
if(!b[edge[i].to])
{
b[edge[i].to]=1;
dfs(i);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
}
for(register int i=1;i<=n;i++)
if(!b[i])dfs(i);
return 0;
} dfs序还是很重要的在二分图，拓扑排序中皆有应用。
出自zh的blog，想要详细了解图论，请点图论
2.flag妙用
大家都知道
是搜索中判断是否合法或是否使用的宝贝，但许多人不知道如何用好。
所以我们用一道题来讲一讲妙用P1074。
我们要满足每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，且不重复。
许多人犯难了，该如何判断？
我们仔细思考：总共就是9x9的格子，填的数也只有1-9，情况并不多，
所以我们设三个
数组 ![line[10][10],list[10][10],nine[10][10]](http://img.e-com-net.com/image/info8/da61f1592f934661b6b9d732a775aff2.gif){kind=small}
分别代表行，列，九宫格中数字1-9使用情况。
行和列都还好，循环判断即可，但九宫格，就需要一个函数
int ninth( int i , int j ) {
if( i <= 3 && j <= 3 ) return 1 ;
if( i <= 3 && j <= 6 ) return 2 ;
if( i <= 3 ) return 3 ;
if( i <= 6 && j <= 3 ) return 4 ;
if( i <= 6 && j <= 6 ) return 5 ;
if( i <= 6 ) return 6 ;
if( j <= 3 ) return 7 ;
if( j <= 6 ) return 8 ;
return 9 ;
}此题详解：P1074 靶形数独题解
3.搜索出金牌算法
这个很好解释，不会的题可以用搜索瞎搞一下，兴许就能AC
如P3958。
出题人可能是想把并查集作为标算，但是经过测试发现，dfs才是最快的。
首先，我们找出所有可以从下表面进入的球，然后深度优先搜一遍。一旦遇到一个点最高处高度
，就表示可以到上表面，退出。因为每个洞最多访问一次（只需要求是否能到达上表面，而不是最短步数），然后决定下一步的时候还需要
的时间。所以总复杂度时
。
至于为什么dfs最快：
实际上，往往不需要访问所有的洞就可以判断“Yes”，大多数情况下只有“No”的情况要访问全部。因此很少达到的最高复杂度。
所以在赛场上程序不会打不要紧，可以试一试搜索。
4.搜索结合其他算法瞎搞
前面dfs序算一种，还有：
搜索+dp P1021
这道题用dfs来拼数，用dp来找最优方案。
#include
#include
using namespace std;
int a[17],n,k,c[17],maxn;
inline int dp(int x,int y)
{
int f[50000];
f[0]=0;
for(register int i=1;i<=a[x]*n;i++)
f[i]=50000;
for(register int i=1;i<=x;i++)
for(register int j=a[i];j<=a[x]*n;j++)
f[j]=min(f[j],f[j-a[i]]+1);
for(register int i=1;i<=a[x]*n;i++)
if(f[i]>n)return i-1;
return a[x]*n;
}
inline void dfs(int x,int y)
{
if(x==k+1)
{
if(y>maxn)
{
maxn=y;
for(int i=1;i<=x-1;i++)
c[i]=a[i];
}return;
}
for(register int i=a[x-1]+1;i<=y+1;i++)
{
a[x]=i;
int y1=dp(x,y);
dfs(x+1,y1);
}
}
int main()
{
scanf("%d%d",&n,&k);
dfs(1,0);
for(register int i=1;i<=k;i++)
printf("%d \n",c[i]);
printf("MAX=%d\n",maxn);
} 5.重点：剪枝
剪枝有两种：可行性剪枝和最优性剪枝
可行性剪枝：
当搜索到一个状态时，如果可以判断这个状态之后的状态都不合法，则直接退出当前状态。一般用于求方案数的题目中。
例如之前的奶酪，就是达到上表面就退出，就让程序跑得很快。
例题：给定一个 
和 
，求满足 
的排列个数。
朴素算法是求出所有的序列，再计数。
但是在这个题中，满足条件是对所有的 i，不等式都要成立，那么换言之，只要有一个 i 不满足之前的不等式，那么排列就是不满足条件的。
所以只要不满足，就退出，就好了，这样就做到了剪枝。
例如之前的P1074。
若暴搜则有几个点过不去，要到2s左右。
所以我们考虑剪枝：
像我这种没玩过数独的乡里人，不知道玩数独有这样一个方法：
从数多的一行开始填，这样要选择的数就少了，不合法的情况就可以省掉一些
所以我们定义一个
（struck），用一个
来存每行
的个数。
用它作为关键字
一遍后，再从最少的开始搜。
最优性剪枝：
当搜索到一个状态时，如果可以判断这个状态之后的状态都不会比当前的最优状态更优，则直接退出当前状态。
例如：P1034。
加一个套路的最优化剪枝就过了啊，矩形不可能重叠，check一下就好了。
6.高级操作：优化
1、记搜
在搜索的时候，如果搜到了之前搜过的状态，而且搜索的结果只与搜索的初始状态有关，那么可以将每一个搜索初始状态所对应的结果记录下来，减少搜索次数，降低时间复杂度。
举个例子，用递归算 Fibonacci 数列复杂度为
如果我们能把每个 fib(n) 记录下来，比如：
int Fib[MAXN];
int fib(int n)
{
if (n <= 1) return n;
else if (Fib[n]) return Fib[n];
else return Fib[n] = f(n - 2) + f(n - 1);
}
那么每个 fib(i) 都只会被算一次，而且可以认为是在 O(1) 的时间内被算出来。 所以总的时间复杂度就变成 了。
2、前缀和优化
如：P2130。
简单一看：看似是正常的广搜，从每个点扩展出长度为
的路径，那么只要暴搜就好了。
这道题数据不大，所以可以过。
但我们考虑一下优化：如何快速求出两个格子中间是否有阻碍：
可以在每一列和每一行维护一个前缀和，障碍设为1，否则设为0，然后在搜索时只需要求一下终点与起点的差，如果是零，则两点联通。
就可以轻松跑过了。