子集生成(无重复集合)------三种方法
给定一个集合,枚举所有可能的子集。集合中没有重复元素。
1.增量构造法
第一种思路是一次选出一个元素放到集合中,程序如下:
用A[i]记录集合S中被选取元素的下标。由于A中记录的元素个数不确定,每次递归调用都要输出当前集合。另外,递归边界也不需要显式确定——如果无法继续添加元素,自然就不会再递归了。下面的代码用到了定序的技巧:规定集合S中所有元素的编号从小到大排列,就不会把集合{1, 2}按照{1, 2}和{2, 1}输出两次了。
提示:在枚举子集的增量法中,需要使用定序的技巧,避免同一个集合枚举两次。
#include
using namespace std;
int A[1000],S[1000];
int len;
void printSubset(int cur) {
for(int i = 0; i < cur; i++) cout<> len;
for(int i = 0;i < len; i++)
cin>> S[i];
printSubset(0);
return 0;
}
2、位向量法(标记)
第二种思路是构造一个位向量B[i],而不是直接构造子集A本身,其中B[i]=1,当且仅当S[i]在子集S中。递归实现如下:
必须当“所有元素是否选择”全部确定完毕后才是一个完整的子集,所以时间复杂度比增量构造法高。
提示:在枚举子集的位向量法中,解答树的结点数略多,但在多数情况下仍然够快。
#include
using namespace std;
bool B[1000];
int S[1000];
int len;
void printSubset(int cur) {
if(cur == len) {
for(int i = 0; i < cur; i++)
if(B[i]) cout<>len;
for(int i=0;i>S[i];
printSubset(0);
return 0;
} 3.二进制法
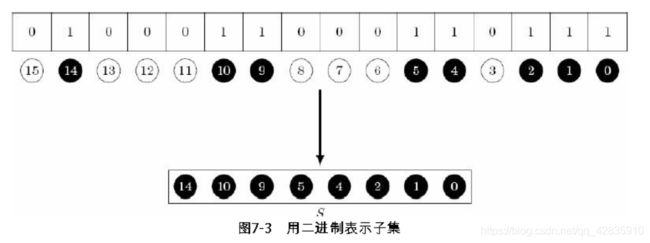
另外,还可以用二进制来表示{0, 1, 2,…,n-1}的子集S:从右往左第i位(各位从0开始编号)表示元素i是否在集合S中。图7-3展示了二进制0100011000110111是如何表示集合{0, 1,2, 4, 5, 9, 10, 14}的。
图7-3 用二进制表示子集
注意:为了处理方便,最右边的位总是对应元素0,而不是元素1。
提示:可以用二进制表示子集,其中从右往左第i位(从0开始编号)表示元素i是否在集合中(1表示“在”,0表示“不在”)。
提示7:当用二进制表示子集时,位运算中的按位与、或、异或对应集合的交、并和对称差。
提示:从代码量看,枚举子集的最简单方法是二进制法。
#include
using namespace std;
int a[1000],num[1000];
void printSubset(int n, int s) { //打印{0, 1, 2,..., n-1}的子集S
for(int i = 0; i < n; i++) //对每次传入的s的二进制进行逐个位数判断
if(s&(1<>n;
for(int i=0;i>num[i];
for(int i = 0; i < (1<