首先,何为最短路?
假设有五个点,每个点之间都有一条连线,并且赋予距离。给予一对起点与终点,让你求出从起点到终点的最短距离,或者最短时间。
HDU2544.
这个问题可以枚举,从1-2,1-3,1-2-3等等并求出其最短的路线,但是如果数据太多怎么办。假如有1000个点,挨个枚举可能会枚举半年,所以这个时候引出几种算法,我们先来看第一种。以下算法我们都以一道题为例题:输入N,M(分别表示终点N,并且有M条边),接下来输入M行x,y,z分别表示从点x到点y的距离为z,求出1-N的最短距离,例如
2 3
1 2 4
1 3 1
2 3 1 输出结果应该是:2 即最短路线为 1-3-2;(如果未特殊情况说明,路线为双向)
一、Dijkstra算法
1.首先,盗图。(如有侵权,立即删除)


2.我们从起点出发,依次遍历与起点相连的每一个点,更新他们与起点的距离,比如该图中,与6的距离会变成14,与3的距离变成9,与2的距离变成7.然后再选择一个与起点距离最短的点,再去更新与之相邻的点,这样由于每次都选择的是最优解(即最短路)所以,每个点都遍历完之后,每个点上面的数值,就是与起点的最短距离。(还不懂就认真看盗的动图)。
3.所以首先加边,然后进行算法,第一个代码有加边环节,剩下的就不写了,只写算法,下面我们看一下求解这道题的Dijkstra算法:
时间复杂度O(n^2) 空间复杂度O(n)
#include
#include
#include
#include
二、Floyd算法
1.首先,再次盗图:

2.我们从图中可以看出如果从1-到4.有3种可能,1-4或者1-3-4或者1-2-3-4.我们基于动态规划的思想,一个点经过点k或者不经过点k距离变不变小。所以这里的状态转移方程应该是 dp[i][j]=dp[i][k]+dp[k][j](经过点k变短)否则dp[i][j]=dp[i][j]。
Floyd算法,时间复杂度O(n^3) 空间复杂度O(n^2)
#include
#include
#include
#include
三、队列求短路【Spfa】
1. 该算法运用C++里的STL库,queue进行逐步更新。
2.首先,还是盗图。
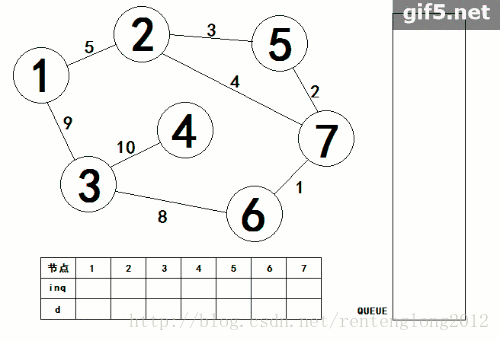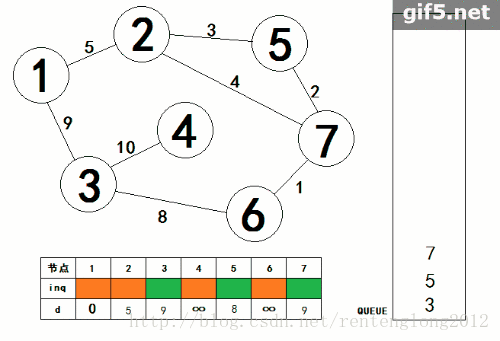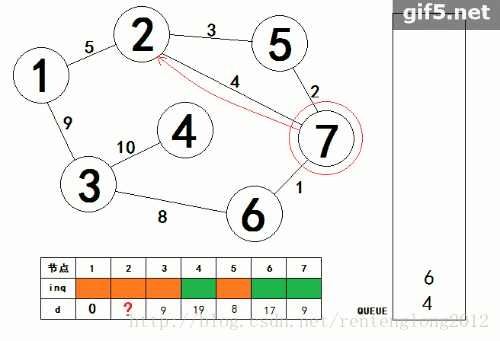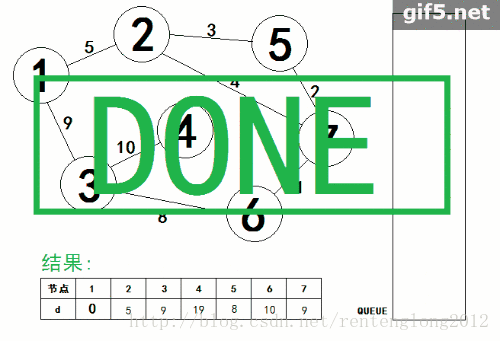
3.运用队列的性质,从起点开始,将与他相连的点遍历,判断这个点是否在队列当中,如果不在队列当中就把这个点加上,在队列中则不能加,只更新他最小距离。
Spfa算法
时间复杂度:O(nlgn)-O(n^2)
#include
#include
#include
#include
四、堆优化队列【priority queue】
根据Dijkstra的思想,每次应该从距离起点最近的点去更新其他点,所以用堆优化求最短路。
时间复杂度 O(nlgn)
#include
#include
#include
#include
五、总结
以上就是全部的在我已知范围内的求最短路的方法,总结一下这些方法的根本都在于,去更新最小距离,Spfa是对Dijistra的优化,而priorityqueue是对queue的优化。Floyd是基于动态规划的思想每次都更新最短路,首先更新自己与其他点的距离,再去更新,经过点K的距离。
最后PS:还需要加油啊!
![]()


