RNN浅析

来源：http://blog.csdn.net/leochen1983/article/details/64133814

参考资料

• A Critical Review of Recurrent Neural Networks for Sequence Learning （2015年的一篇综述性文章）

• Long Short-Term Memory in RNN （Felix Alexander Gers大牛的博士论文）

• Supervised sequence labelling with recurrent neural network （Alex Graves大牛的springer出版物）

• Deep Learning（Yoshua Bengio大神的基础教程）

---

目录

• 一、简述

• 二、RNN基础算法

• 三、LSTM以及LSTM的变种

---

一、简述

循环神经网络（Recurrent neural networks，简称RNN）是一种通过隐藏层节点周期性的连接，来捕捉序列化数据中动态信息的神经网络，可以对序列化的数据进行分类。和其他前向神经网络不同，RNN可以保存一种上下文的状态，甚至能够在任意长的上下文窗口中存储、学习、表达相关信息，而且不再局限于传统神经网络在空间上的边界，可以在时间序列上有延拓，直观上讲，就是本时间的隐藏层和下一时刻的隐藏层之间的节点间有边。RNN广泛应用在和序列有关的场景，如如一帧帧图像组成的视频，一个个片段组成的音频，和一个个词汇组成的句子。尽管RNN有一些传统的缺点，如难以训练，参数较多，但近些年来关于网络结构、优化手段和并行计算的深入研究使得大规模学习算法成为可能，尤其是LSTM与BRNN算法的成熟，使得图像标注、手写识别、机器翻译等应用取得了突破性进展。 

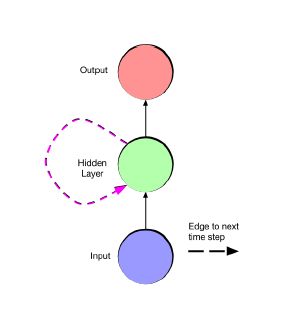
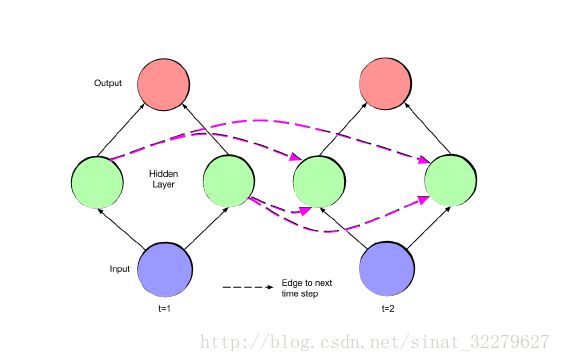
最简单的RNN（fold状态和unfold状态）

注意：输入层、隐藏层、输出层的比例不一定是1：1：1,(fold状态和unfold状态)

注意：输入层、隐藏层、输出层的比例不一定是1：1：1,(fold状态和unfold状态)

1. WHY——关于序列化（sequentiality）的几个问题

1.为什么需要进行显式表达序列模型？

传统的机器学习方法，如SVM、logistics回归和前向神经网络都没有将时间进行显式模型化，用这些方法建模而得出的好的实验结果都是基于独立性假设的前提。还有一些模型将本节点和时间上的前驱节点与后继节点相连接，通过上下文的滑动窗口来将时间隐式模型化，例如深度置信网络DBN。尽管独立性假设非常有用，但是这些模型排除了长时依赖（long-range dependencies）的实际情况。比如用时间窗口大小为5进行训练的模型无法回答需要6个时间输入的问题。人机对话系统、现代交互系统都需要将序列化模型或时间模型显式表达，否则任何分类器或回归器都是无法组合起来解决这种问题的。

2.为什么不用Markov模型？

RNN并非唯一一个将时间依赖显式表达的模型，Markov链也包含时间信息（或说是观测序列），但它有一定局限性。首先，离散状态空间必须是有限尺寸，而不是无限，因为动态规划算法在运算复杂度上是状态空间尺寸的平方；其次，转移表的大小（两个任意时间点的状态转移轨迹概率）也是状态空间尺寸的平方，如果隐藏状态数量较大，运算复杂度呈平方数增长；最后，隐藏状态仅依赖此刻的上一个状态，而不是多个前次的状态，即便可以设定窗口来与多个先前状态建立关系，但状态空间的增长随窗口的大小成指数性增长，使得长时依赖（long-range dependencies）的建模计算变得不切实际。

相比之下全连接的ANN模型没有上述问题，首先RNN可以捕捉长时依赖信息，和Markov链相比传统RNN的一个状态依赖于当前输入和上一个时间步骤的网络状态，隐藏层包含任何时间点的网络状态信息，几乎相当于任意长度的时间上下文。而且不同状态的数量可以随隐藏层的节点数增长而指数增长，即便每个节点仅能2值表示，N个隐藏层节点也可表示2的N次幂个状态，若节点是实数则表达的不同状态的数量更多。所以说潜在的表达能力随着节点数的增长而指数的增长，推演和训练的复杂度也成二次方增长

3.RNN是否非常有表现力？

有限尺寸的RNN和非线性激活函数可以组建大量的模型，几乎可以拟合任意函数，甚至是通用图灵机。Hava T. Siegelmann and Eduardo D. Sontag. Turing computability with neural nets. Applied Mathematics Letters, 4(6):77-80, 1991.体现了强大的计算表现力，虽然C语言几乎可以编写任何程序，也有很强大的表现力。但实际上C语言并非机器学习的灵丹妙药，其中一个原因就是C语言开发并不容易并不高效，比如没有一个C语言实现的通用方法来求损失函数的梯度。此外给定一个有限数据集，有很多程序可以过耦合去生成想要的训练结果，但是却无法生成test例子。 
为什么RNN没有上述问题呢，首先，即便架构确定好，即节点数、边界与激活函数固定，RNN也会体现出端到端的不同，损失函数可以对任意权值进行求导，使得RNN可以进行基于梯度的训练；其次，RNN一大特性就是图灵完全，C语言程序无法通过复制来生成出任意程序；最后，不同于C语言编写的程序，RNN可以通过标准手段进行正则化如weight decay、dropout、阶数限制等避免过饱和。

2. HOW——关于序列化方式，即如何给序列进行标签化（sequence labeling）的问题

对序列进行标签化（sequence labeling）是RNN比较关键的问题，如语音识别、手写识别的边界标记，以及非时域上的蛋白质结构预测。对于给定输入的标签边界划分应该是由学习算法来确定的，这是算法的一个难点因为有些场景不能通过手动或自动化的预处理过程事先确定边界，而又有些场景我们只关系输出的标签的序列，边界似乎并不重要，标签并不一定非常精确的出现在发生的时间点上或输入的边界上。

如下图所示，sequence分类输入是一个片段，输出是一个标签，它是segment分类的一种特殊情况；segment分类输入是有边界且边界位置任意的序列，输出是有边界且边界位置任意的序列，它是segment分类的一种特殊情况，属于strongly labelled；temporal分类输入是无边界的序列，输出是有边界且边界位置任意的序列，属于weaklly labelled，

sequence分类:该分类中固定长度输入，单个的输入向量，如MNIST。对于输入数据旋转变换的不变性，可用multidimensional recurrent neural networks去解决。sequence分类错误率表示如下

segment分类:输入是离散可分割的，输出也是一个序列，有多个标签，例如NLP，上下文信息是至关重要的，对于边界不清晰的可以用时间窗口，错误率用汉明矩来表示。在语音识别中，音频帧作为一个segment，在图像处理中，一块区域内的像素点为一个segment。segment分类错误率表示如下

temporal分类:除了label序列的长度小于输入序列之外，没有任何其他假定，segment分类起码会通过算法来决定输入序列从哪儿开始到哪儿结束，而temporal分类则没有，这就需要显式或隐式模型来掌握的全局结构。temporal分类错误率如下

此外,根据输入输出的序列关系，RNN可以表达如下几种结构（全部是unfold状态）：

(1)非RNN (2) 一对多 (图像标注，输入是图像，输出是多个词汇组成的句子). (3) 多对一 (语句情感分析，输入是一句话，输出是正负情感判断). (4) 多对多 (机器翻译). (5) 同步多对多 (视频分类，输入是视频帧，输出是一些标签）

注意：输入层、隐藏层、输出层的比例不一定是1：1：1,(fold状态和unfold状态)

二、RNN基础算法

首先提出RNN的是Hopfiled，文章为 
*John J. Hopfeld. Neural networks and physical systems with emergent collective 
computational abilities. Proceedings of the National Academy of Sciences, 79 
(8):2554-2558, 1982.* 
前向网络结构是Boltzmann machines和auto-encoders

第一次提出对sequences进行监督学习的是Jordan，该结构有两个突出的特点 
(1). 输出节点对隐藏节点也有反馈；(2). 隐藏层节点有self-connected，文章为Michael I. Jordan. Serial order: A parallel distributed processing approach.Technical Report 8604, Institute for Cognitive Science, University of California,San Diego, 1986. 
Elman简化了这种结构，输出节点不再直接对隐藏节点做反馈，名称也有了变化，对于fold状态的隐藏节点单元称为”context node”替换了”state node”。该种结构是下一节LSTM等算法的基础，文章为Jerey L. Elman. Finding structure in time. Cognitive science, 14(2):179-211,1990.

学习过程被认为是NP完全的，难点尤其是在长距离的依赖上，而在反向多次求导的过程中还会出现梯度消失或梯度暴增的现象，研究者们认为必须对参数进行正则化，并限制权值的范围来避免梯度变化过快的问题。主流参数训练的方法是通过穿越时间的反向求导来实现的，称为（backpropagation through time，BPTT）算法，文章为Paul J. Werbos. Backpropagation through time: what it does and how to do it.Proceedings of the IEEE, 78(10):1550-1560, 1990. Williams和Zipser在此基础上做了改进，提出了TBPTT算法，该算法可以减轻梯度暴增的问题，而LSTM算法彻底解决了梯度消失的问题，具体会在下一节做详细的阐述。 
局部最优的问题是有效训练最大的障碍，而且是无法通过修改网络架构来解决的，即便是单层隐藏层前向网络也是NP问题，最近的经验和理论研究表明 
这种问题一次性解决并不是很重要。许多极值点在大规模神经网络的误差表面上，局部最小值的鞍点比率随着网络的增大指数性的增长，算法可以被设计成尽量去避开鞍点。 
前向算法

后向算法

此外，还有一种Hessian-free truncated的牛顿方法，牛顿方法要计算Hessian矩阵，对于大规模的网络来说参数非常多，而该算法仅仅估计Hessian矩阵，即便如此相对于SGD还是很耗费计算量，但是的确能够弥补SGD的部分不足。

三、LSTM以及LSTM的变种

LSTM

正如上一节所述，RNN面临的第一大问题即是对长跨度时间可能会有梯度消失或爆发的问题的问题，

BPTT（Back propgation through time)中从t+1到t时刻的误差信号计算如下

从t时刻的u节点到t-q时刻的v节点的误差传递信号为

把连乘展开

把连乘的用T来表示

结果对T求和的次数是n的q-1次幂，即n的q-1次幂个T，每个T需要q次下面的乘法

如果上式> 1, 误差就会随着q的增大而呈指数增长，那么网络的参数更新会引起非常大的震荡。 
如果上式< 1， 误差就会消失，导致学习无效，一般激活函数用sigmoid函数，它的倒数最大值是0.25, 权值最大值要小于4才能保证不会小于1。 
误差呈指数增长的现象比较少，误差消失在BPTT中很常见。

以上的推导过程，参考了Sepp Hochreiter. “The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions..” International Journal of Uncertainty Fuzziness and Knowledge-Based Systems 6.2(1998):107-116..

于是诞生了long short term memory network的方法 LSTM Sepp Hochreiter and Jurgen Schmidhuber. Long short-term memory. Neural Computation, 9(8):1735-1780, 1997.和Gustavsson, Anders, et al. “On the difficulty of training Recurrent Neural Networks.” Indian Journal of Microbiology 52.3(2012):337-345.

长时记忆：对于权重（weights）来说，在训练过程中变化比较缓慢 
短时记忆：对于激活函数（activation）来说，从一个节点到另一个节点是短暂的 
LSTM利用cell来存储一些值，并可控制其输入、遗忘和输出 
cell是用来替换node的

在Alex大神的描述下，cell结构如下：

细胞自己有状态，并能通过内部更新的方式更改自己的状态，而门（gate）解雇来对细胞状态增加或者删除信息，门分为输入门、输出门和遗忘门

unfold如下：

梯度变化情况表示：

但上个图比较抽象，并且符号使用也比较混乱 
colah’s blog的图更为直观 
注意符号含义对照：

将隐藏层中的节点放大来看（目前设定每个时间t的隐藏层仅一个节点A），输入输出都是向量

将内部透明化来看如下图，其中粉色节点是point-wise（即element-wise）

细胞的状态在节点中发生改变，并将改变传递给下一时刻的该层，这种变化是通过point-wise的乘性操作和加性操作来完成的，这个图在Alex的fold图中表现的比较混乱

遗忘门决定细胞中遗弃何种信息，1为保留，0为遗忘

细胞存储何种信息由两部分决定，输入门的结果（sigmoid）以及新的候选向量（tanh）

细胞更新如下

细胞输出如下

LSTM 变种

1.peephole变体

在所有门上加了peephole

前向算法：

后向算法：

具体内容详见Gers, Felix A., and J. Schmidhuber. “Recurrent Nets that Time and Count.” Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks (IJCNN’00)-Volume 3 - Volume 3 IEEE Computer Society, 2000:3189.

2.配对遗忘与输入门

该算法将决定遗忘和添加信息两个过程进行了归并，即输入新的内容一定会忘记旧的内容，从而简化了算法

3. Gated Recurrent Unit

该算法将输入门和遗忘门结合成了更新门，并且合并了细胞状态和隐含状态，在不减少功能的同时简化了算法

具体内容详见Cho, Kyunghyun, et al. “Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation.” Eprint Arxiv (2014).

4. 其他

此外还有Depth-Gated Recurrent Neural Networks、A Clockwork RNN等变种，LSTM: A Search Space Odyssey、An Empirical Exploration of Recurrent Network Architectures对变种做了比较。

注意：输入层、隐藏层、输出层的比例不一定是1：1：1,(fold状态和unfold状态)