面试突击——数据结构基础,排序
在待排序的文件中,若存在多个关键字相同的记录,经过排序后这些具有相同关键字的记录之间的相对次序保持不变,该排序方法是稳定的,若具有相同关键字的记录之间的相对次序发生变化,则称这种排序方法是不稳定的。
选择排序:包括简单选择排序和堆排序。
1 简单选择排序
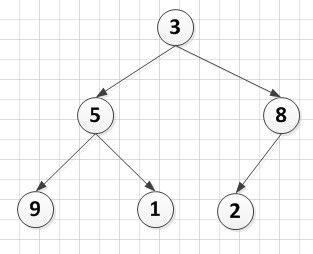
示例:假设给定数组A[1......6]={ 3,5,8,9,1,2 },我们来分析一下A数组进行选择排序的过程
第一趟:i=1,index=5, a[1] 和 a[5] 进行交换。得到序列:{ 1,5,8,9,3,2 }
第二趟:i=2,index=6, a[2] 和 a[6] 进行交换。得到序列:{ 1,2,8,9,3,5 }
第三趟:i=3,index=5, a[3] 和 a[5] 进行交换。得到序列:{ 1,2,3,9,8,5 }
第四趟:i=4,index=6, a[3] 和 a[5] 进行交换。得到序列:{ 1,2,3,5,8,9 }
第五趟:i=5,index=5, 不用交换。得到序列:{ 1,2,3,5,8,9 }
(6-1)趟选择结束,得到有序序列:{ 1,2,3,5,8,9 }
描述:给定待排序序列A[ 1......n ] ,选择出第i小元素,并和A[i]交换,这就是一趟简单选择排序。
性能分析:不论最坏还是最佳情况,比较次数都是一样的,所以简单选择排序平均时间,最坏情况,时间复杂度O(n^2)。
简单选择排序是稳定的排序。
2 堆排序——相对于选择排序来说,主要目的是减少比较次数
堆:一棵完全二叉树且满足性质:所有非叶子结点的值均不大于或均不小于其左、右孩子结点的值。
过程描述:1、建堆 2、将堆顶记录和堆中最后一个记录交换 3、筛选法调整堆,堆中记录个数减少一个,重复第2步。整个过程中堆是在不断的缩减。
堆排序是不稳定的原地排序算法。
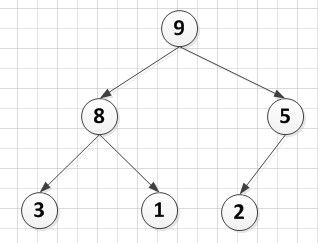
这个堆可以看成是一个一维数组A[6]={9,8,5,3,1,2},那么相应的这个数组需满足性质:A[i]<=A[2*i] && A[i]<=A[2*i+1] 。其中A[i]对应堆中的非叶子结点,A[2*i]和A[2*i+1]对应于左右孩子结点。并且最后一非叶子结点下标为[n/2]向下取整。
调整:
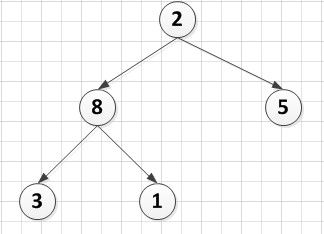
把9跟2互换,同时把a[6]这个结点从堆中去掉,于是得到下面这个完全二叉树。
A[5]={2,8,5,3,1}
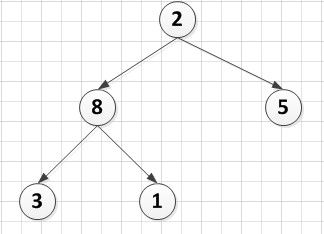
比较根结点和左、右孩子的值,若根结点的值不小于孩子结点的值,说明根结点并没有破坏堆的性质,不用调整;若根结点的值小于左右孩子结点中的任意一个值,则根结点与孩子结点中较大的一个互换,互换之后又可能破坏了左或右子树的堆性质,于是要对子树进行上述调整。这样的一次调整我们称之为一次筛选。
A[5]={2,8,5,3,1}
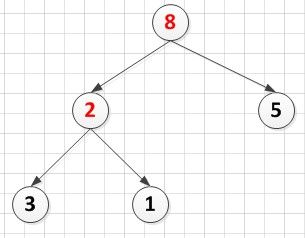
A[5]={8,2,5,3,1}
A[5]={8,3,5,2,1}
建堆:
A[6]={3,5,8,9,1,2},怎样使它变成一个堆呢?
仔细想一想筛选法的前提条件是什么:根结点的左右子树已经是堆。那么这棵树中哪个结点的左右子树是堆呢,很自然的发现是最后一个非叶子结点,所以我们在这里需要自下而上的调整这个完全二叉树。
A[6]={3,9,8,5,1,2}
时间分析:堆排序时间=建堆时间+调整堆时间。从上文中知道建堆时间复杂度为O(n*log2n)。筛选法调整堆(maxHeap函数)时间O(log2n),总共循环了n-1次maxHeap函数,所以调整堆时间复杂度为O(n*log2n)。得出堆排序时间复杂度O(n*log2n)。
堆排序的本质和选择排序的本质是一样的。选择一个待排序序列中的最小(大)值,这就是选择排序的本质。
插入排序,包括:直接插入排序、折半插入排序、表插入排序、希尔插入排序