Kth Ancestor of a Tree Node

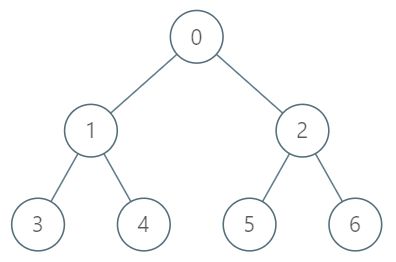
You are given a tree with n nodes numbered from 0 to n-1 in the form of a parent array where parent[i] is the parent of node i. The root of the tree is node 0.

Implement the function getKthAncestor(int node, int k) to return the k-th ancestor of the given node. If there is no such ancestor, return -1.

The k-th ancestor of a tree node is the k-th node in the path from that node to the root.

Example:

 

Input:
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

Output:
[null,1,0,-1]

Explanation:
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2);  // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3);  // returns -1 because there is no such ancestor

Constraints:

• 1 <= k <= n <= 5*10^4
• parent[0] == -1 indicating that 0 is the root node.
• 0 <= parent[i] < n for all 0 < i < n
• 0 <= node < n
• There will be at most 5*10^4 queries.

思路：正确的解法应该是binary lifting；具体看这个视频：https://www.youtube.com/watch?v=02zM-QoKoPg

以2的倍数往上找；这是个新的知识点，需要掌握；九章没讲过；

class TreeAncestor {
    private HashMap> graph;
    private int[][] father;
    public TreeAncestor(int n, int[] parent) {
        // binary lifting, fa[i][j]表示：i点的2^j的往上的祖先是谁；
        this.father = new int[n][30];
        graph = new HashMap<>();
        for(int i = 0; i < n; i++) {
            Arrays.fill(father[i], -1);
            graph.put(i, new ArrayList());
        }
        for(int i = 1; i < n; i++) {
            graph.get(parent[i]).add(i);
            father[i][0] = parent[i];
        }
        dfs(0);
    }
    
    private void dfs(int cur) {
        for(int i = 1; father[cur][i - 1] >= 0; i++) {
            father[cur][i] = father[father[cur][i - 1]][i - 1];
        }
        for(int next: graph.get(cur)) {
            dfs(next);
        }
    }
    
    public int getKthAncestor(int node, int k) {
        // k往左shift几位，i就增加了几个；
        for(int i = 0; k > 0; i++, k>>=1) {
            if((k & 1) > 0) {
                node = father[node][i];
                if(node < 0) {
                    return -1;
                }
            }
        }
        return node;
    }
}

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor obj = new TreeAncestor(n, parent);
 * int param_1 = obj.getKthAncestor(node,k);
 */

思路：刚看了解答，无语了，竟然直接存个parent的depth信息就可以过。估计直接height[node] < k 这个判断，省去了很多时间；因为搜索的话，还是个log(n)的搜索；findHeight用到了记忆化递归；

class TreeAncestor {

    private int n;
    private int[] parent;
    private int[] height;
    public TreeAncestor(int n, int[] parent) {
        this.n = n;
        this.parent = parent;
        this.height = new int[n];
        for(int i = 0; i < n; i++) {
            findHeight(i);
        }
    }
    
    private int findHeight(int node) {
        if(node == 0 || height[node] != 0) {
            return height[node];
        }
        height[node] = height[parent[node]] + 1;
        return height[node];
    }
    
    public int getKthAncestor(int node, int k) {
        if(height[node] < k) {
            return -1;
        }
        int res = node;
        while(k > 0) {
            res = parent[res];
            k--;
        }
        return res;
    }
}

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor obj = new TreeAncestor(n, parent);
 * int param_1 = obj.getKthAncestor(node,k);
 */