CodeForces580C Kefa and Park 【dfs vector】
C. Kefa and Park
time limit per test2 seconds
memory limit per test256 megabytes
inputstandard input
outputstandard output
Kefa decided to celebrate his first big salary by going to the restaurant.
He lives by an unusual park. The park is a rooted tree consisting of n vertices with the root at vertex 1. Vertex 1 also contains Kefa’s house. Unfortunaely for our hero, the park also contains cats. Kefa has already found out what are the vertices with cats in them.
The leaf vertices of the park contain restaurants. Kefa wants to choose a restaurant where he will go, but unfortunately he is very afraid of cats, so there is no way he will go to the restaurant if the path from the restaurant to his house contains more than m consecutive vertices with cats.
Your task is to help Kefa count the number of restaurants where he can go.
Input
The first line contains two integers, n and m (2 ≤ n ≤ 105, 1 ≤ m ≤ n) — the number of vertices of the tree and the maximum number of consecutive vertices with cats that is still ok for Kefa.
The second line contains n integers a1, a2, …, an, where each ai either equals to 0 (then vertex i has no cat), or equals to 1 (then vertex i has a cat).
Next n - 1 lines contains the edges of the tree in the format “xi yi” (without the quotes) (1 ≤ xi, yi ≤ n, xi ≠ yi), where xi and yi are the vertices of the tree, connected by an edge.
It is guaranteed that the given set of edges specifies a tree.
Output
A single integer — the number of distinct leaves of a tree the path to which from Kefa’s home contains at most m consecutive vertices with cats.
Examples
inputCopy
4 1
1 1 0 0
1 2
1 3
1 4
output
2
inputCopy
7 1
1 0 1 1 0 0 0
1 2
1 3
2 4
2 5
3 6
3 7
output
2
Note
Let us remind you that a tree is a connected graph on n vertices and n - 1 edge. A rooted tree is a tree with a special vertex called root. In a rooted tree among any two vertices connected by an edge, one vertex is a parent (the one closer to the root), and the other one is a child. A vertex is called a leaf, if it has no children.
Note to the first sample test:
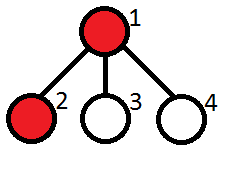
The vertices containing cats are marked red. The restaurants are at vertices 2, 3, 4. Kefa can’t go only to the restaurant located at vertex 2.
Note to the second sample test:
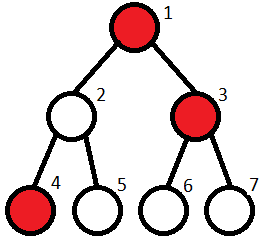
The restaurants are located at vertices 4, 5, 6, 7. Kefa can’t go to restaurants 6, 7.
思路:Kafe的家在树的顶点,每个叶子节点都是一个餐厅。但是沿途不能连续进过m只猫,求最后能到达的餐厅个数。
首先用vetcor数组记录每一个顶点可以到达的点,开始以为形容变的时候,是father son的顺序,但样例中是有后面的节点小于前面的节点,所以应该作为一个无向图处理。当遍历玩所有tree[node]中的节点后,即走完了一条路径。
/*
invalid types 'int[int]' for array subscript 出现了这个错是因为变量名和数组名都要用的cat导致
*/
#include::iterator it;
vector<int> tree[100005];
void dfs(int node,int cats);//第一个参数表示遍历到第几个节点,第二个表示累计多少个连续的猫
int main()
{
cin>>n>>m;
int temp1,temp2;
for(int i = 1;i<=n;i++)
{
cin>>cat[i];
}
for(int i = 1;i<=n-1;i++)
{
cin>>temp1>>temp2;
tree[temp1].push_back(temp2);
tree[temp2].push_back(temp1);
}
vis[1] = 1;//标记根节已经访问过
dfs(1,cat[1]);
cout<void dfs(int node,int cats)
{
vis[node] = 1;
if (cats>m) return ;
int ok = 1;
for(int i = 0;iif(!vis[tree[node][i]])//仍有没有访问过的点
{
ok = 0;
if(cat[tree[node][i]])//该结点有猫
{
dfs(tree[node][i],cats+1);
}
else
dfs(node[tree][i],0);//如果当前没有猫 则归为零,因为m是指的连续的m只猫
}
}
cnt += ok;
return ;
}
这道题实在是折腾的久,就是对于数据结构掌握的不够好,对于这种较简单的题,没有一眼看出来构造树的数据结构。开始尝试用队列来记录每一个子节点。但是进行出队入队操作前后,结构体的内容并没有变化。。。。神奇。大佬指点,是因为对于队列的操作是对一个副本进行操作,并不会改变原来结构体的值。
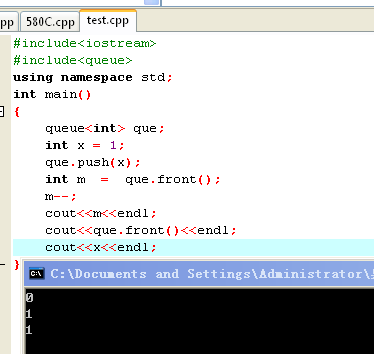
可见对于队首元素的操作并没有真的影响原来x的值。
top.mao = node[top.father].mao + top.data;
node[top.xuhao].mao = top.mao;//!!!重要 第二句话则是知道后,将改变的top.mao真正的赋值到node[top.node].mao。
其实还有问题。。。
我对于边的记录的时候,默认为前面是father 后面是son是不对的,比如两个边
1 2
3 2
按我的存储方法则1是2的父亲,3是2的父亲,但是画图则知,其实3是一个叶子节点。所以有问题。
/*
4 1
1 1 0 0
1 2
1 3
1 4
7 1
1 0 1 1 0 0 0
1 2
1 3
2 4
2 5
3 6
3 7
*/
#include
#include
// }
// cout<
node[1].father = 0;
node[0].mao = 0;
queue
// }
cout<return 0;
}