第一次尝试使用Python创建季节性ARIMA模型
Python构建时间序列ARIMA模型
- 前言
- ARIMA模型简介
- Python实现ARIMA模型预测
- 数据的获取与准备
- 绘制1995-2002年时间序列趋势图
- 去均值化后ADF平稳性检验以及差分
- 绘制自相关函数以及偏相关函数图确定参数p、q
- 建立季节性时间序列模型ARIMA(k,D,m)S×(p,d,q)
- 模型预测
- 模型指标MAPE
- 预测值和真实值趋势对比图
- 结尾
前言
时间:19/04/25,天气晴,心情愉悦。
大学生活不知不觉已经快要结束了,我才第一次认真的开始检查、审视自己过去两年中究竟学到了些什么?仔细回想,学的东西好像还蛮多的,从我开始懵懂学习C语言后入坑编程系列学习以来,自己慢慢的喜欢上这一领域,开始用C实现一些小小的功能,例如12306抢票、一些经典的小游戏等。后续除了掌握一些基本数据库知识之外我又接触了Java这种oo语言,并且我在自己的课程设计里面独立编写了基于MINA框架的商城Shopping微信小程序,虽然写的有点烂,但是也基本实现了商城的大部分功能(对自己要求有点低)。再后来一次侥幸的机会跟着导师做了一个项目,是基于计算机视觉的智能小车导航避障的,为此,我专门去学习了在MFC框架下用opencv实现图像处理,嗯,opencv图像处理是我学了最长时间也是最系统的学习,从简单的图像形态学处理、图像去燥、图像分割到复杂颇具挑战的模式识别我都有了解过研究过,在做图像处理的过程中,我慢慢的发现自己对图像数据(数据)的各式各样处理计算颇感兴趣。那时候正值大数据的热潮,我从网上找了一些大数据的视频学习了Hadoop、Spark等,掌握了大批量数据下并行处理的方式,但是自己并不知道用什么方法去处理数据,于是,18年的下半年,我开始正式接触机器学习领域,至今学习机器学习时常也有半年的时间了,在这半年里也学习了很多公式推导也有很多算法流程,如今让我回忆一下自己曾经学的这些机器学习的东西,自己的印象其实已经没有那么深刻了,即使在学习当下对算法推导以及应用非常的熟悉,但是没有把自己学的内容整理下来,即使学过随着时间推移也差不多把大部分细节给忘记了。我挺后悔自己当初学习的时候没有做笔记,不过悔在过去、行在当下,从此刻开始记录我的学习,我相信我可以坚持记录下去。
ARIMA模型简介
具有如下结构的模型称为求和自回归移动平均(Autoregressive Integrated Moving Average),简记为ARIMA(p,d,q)模型:

式中:

ARIMA模型的数学原理和公式我就不一一解释了,如果有不懂的地方可以参考ARIMA模型,在本篇中我们主要探讨如何用Python对时序进行分析建模。
Python实现ARIMA模型预测
数据的获取与准备
如某市1995-2003年各月的工业生产总值如下表所示,试对1995-2002年数据建模,2003年的数据留做检验模型的预测结果。

我们在获取数据时,可能会因为一些客观因素(比如一些表格编辑软件的自动将编码转换UTF-8,默认的时间格式规范不一致,例如19/04/25可能会转换成04/25/19,还有就是本身数据就存在缺失、不合理等问题)导致了数据的异常或缺失,然而在机器学习里,数据的好坏直接决定了模型结果的好坏,所以对数据的预处理必不可少。在我们这个实验数据中,数据并没有出现缺失以及不符逻辑的情况,所以我们可以直接将其作为ARIMA模型的输入数据。(如果数据出现缺失不合理等现象,可以选择性参考 https://blog.csdn.net/zhangyonggang886/article/details/80901290)
Python3:
import csv
data_files = csv.reader(open('data.csv','r'))
dataSet = [] # 训练数据集
dateSet = [] # 训练年份集
for data in data_files:
if data[0] == '200301': # 将csv文件中验证数据去除
break
if data[0] != 'date':
dateSet.append(data[0])
dataSet.append(float(data[1]))
绘制1995-2002年时间序列趋势图
显示一行一行的数据是难以观察数据的趋势走向,这样不利于我们观测数据之间的相互联系,因此画出趋势图有利于数据分析。
Python3:
# 利用Pandas库来绘制时间序列趋势图
import matplotlib.pyplot as plt
import pandas as pd
df = pd.DataFrame(dataSet,index=dateSet,columns=['real value'])
df.plot()
plt.show()
去均值化后ADF平稳性检验以及差分
①为什么要去均值化?做数据的去均值化其实就是对数据进行标准化,在很多情况下,我们对数据本身大小并不感兴趣,我们感兴趣的是数据之间的联系,去均值化并不会影响这种联系,因为去均值化后得到的时间序列趋势和没有去均值化得到的时间序列趋势是一样的。
Python3:
# 对时间序列进行去均值化
mean = sum(dataSet)/len(dataSet) # 计算均值
dataSet_kill_mean = [data - mean for data in dataSet] # 得到去均值后的序列
②序列平稳是做ARIMA回归的前提条件,所以我们得到的序列必须是平稳的。观测上面的序列趋势图,我们可以很明显的发现数据有逐渐上升的趋势,因此我们判断该段时间序列为非平稳序列。为了得到平稳的时间序列,我们要做差分,因为差分目的是使变量序列平稳。
Python3:
# 进行一阶差分并绘制趋势图
df_kill_mean = pd.DataFrame(dataSet_kill_mean,index=dateSet,columns=['kill mean value'])
df_kill_mean_1 = dataSet_kill_mean.diff(1).dropna()
df_kill_mean_1.plot()
plt.show()
result:

③ADF检验可以让我们判断某段时间序列是否为平稳序列(具体ADF统计学原理可以选择性参考http://www.tinysoft.com.cn/TSDN/HelpDoc/display.tsl?id=12889)
Python3:
import statsmodels.tsa.stattools as ts
adf_summary = ts.adfuller(np.array(df_kill_mean_1).reshape(-1)) # 进行ADF检验并打印结果
print(adf_summary)
>>> (-3.3635866783352, 0.012264631212932628, 12, 82, {'1%': -3.512738056978279, '5%': -2.8974898650628984, '10%': -2.585948732897085}, 237.8874357065477)
如何观察上面的统计结果来判断序列是否为平稳呢?
- 1%、5%、10%不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设,本数据中,adf结果为-3.3635866783352, 大于1% level的-3.512738056978279,但小于5% level的-2.8974898650628984,如果建模对序列平稳性有相当高的要求,则认为该序列不平稳,若要求并不严格也可认为该序列是平稳序列。如果一阶差分序列不平稳,则继续做二阶差分并检验。
- P-value是否非常接近0。本结果中,P-value 为 0.012264631212932628 < 0.05并接近0。
由此,通过检验观测值,我们认为上述一阶差分后得到的数据满足平稳性检验要求。(一阶差分后的序列平稳性不太好,有可能通不过白噪声检验,在这里忽略白噪声检验环节,若白噪声检验得到的P值大于0.05,那么我们就得对时间序列进行二阶差分)
绘制自相关函数以及偏相关函数图确定参数p、q
参数确认规则:(已知序列为一阶差分)
① 当偏自相关函数呈现p阶拖尾,自相关函数呈现q阶拖尾时,我们可以选用模型ARIMA(p,1,q)
② 当偏自相关函数呈现拖尾,自相关函数呈现q阶截尾时,我们可以选用模型MA(q)
③ 当偏自相关函数呈现p阶截尾,自相关函数呈现拖尾时,我们可以选用模型AR(p)
(备注:如果想要深入了解如何通过PACF和ACF函数图确定模型以及参数,可以参考《ARMA模型的自相关函数和偏自相关函数图谱》链接:https://pan.baidu.com/s/1JqkIIh1gdHqjp9uwwGC87A 提取码:1koe (如果链接失效,联系我重新发链接)
Python3:
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 绘制自相关图
plot_acf(df_kill_mean_1,lags=24).show() # 其中lags参数是指横坐标最大取值
# 绘制偏相关图
plot_pacf(df_kill_mean_1,lags=24).show()
plt.show()
rusult:
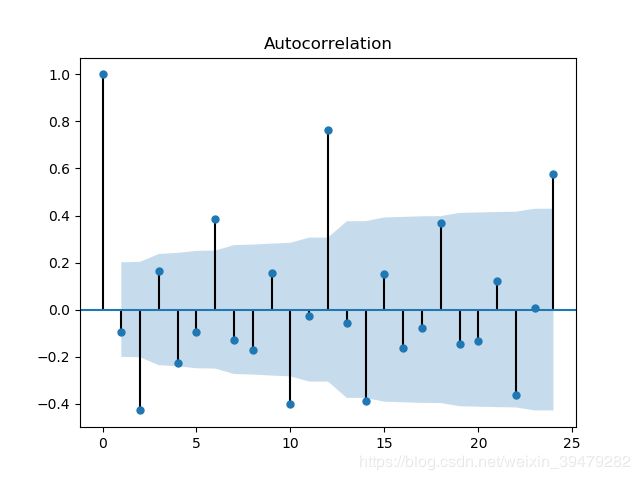
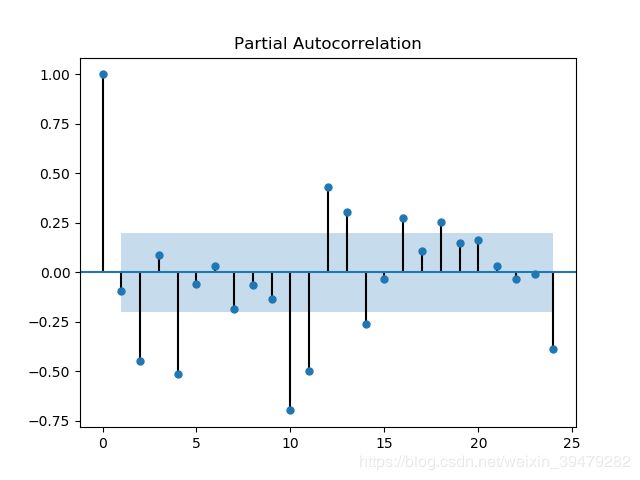
我们观测ACF函数图和PACF函数图,我们发现并没有呈现很好的拖尾或截尾情况。出现这个情况的原因有很多种情况,我们观测函数图发现,每隔一个周期,ACF和PACF都出现“尖峰“,例如上述图每隔12个月出现一个"尖峰",由此我们可以很容易的判断,该序列可能存在季节性影响的因素(其实由开始的序列趋势图我们也可以看出序列存在季节性影响)。
我们可以通过分解的方式将时序数据分离成不同的成分,它主要将时序数据分离为Trend(成长趋势)、seasonal(季节性趋势)、Residuals(随机成分)。然后我们分别对这三个分离的序列进行ARIMA建模得到较好的模型,最后再将模型相加便可以得到最后的ARIMA模型。
Python3:
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(df_kill_mean_1, freq=12)
trend = decomposition.trend # 趋势部分
seasonal = decomposition.seasonal # 季节性部分
residual = decomposition.resid # 残留部分
decomposition.plot()
result:

这种分解建模的方式有些复杂,接下来我们采用季节性时间序列来对上述具有明显季节性的序列进行建模。
建立季节性时间序列模型ARIMA(k,D,m)S×(p,d,q)
我们称ARIMA(k,D,m)S×(p,d,q)为乘积季节模型,也可以写成ARIMA(p,d,q)(k,D,m)S模型,其中S为季节性周期。如果将模型中的AR因子和MA因子分别展开,可以得到类似的ARMA(kS+p,mS+q)的模型。当我们考虑用ARIMA(p,d,q)(k,D,m)S模型的时候,我们需要优化感兴趣度量的是ARIMA(p,d,q)(k,D,m)s各个参数的值。接下来,我们将使用“网格搜索”来迭代地探索参数的不同组合。 对于参数的每个组合,我们使用statsmodels模块的SARIMAX()函数拟合一个新的季节性ARIMA模型,并评估其整体质量。
Python3:
# 这段代码借鉴了其他博文的做法
import itertools
p = q = range(0, 2) # p、q一般取值不超过2
d = range(1,2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
warnings.filterwarnings("ignore") # 忽略警告信息
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(df_mean_1,
order=param,
seasonal_order=param_seasonal,
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print('ARIMA{}x{} - AIC:{}'.format(param, param_seasonal, results.aic))
except:
continue
>>>
ARIMA(0, 1, 0)x(0, 1, 0, 12) - AIC:322.6198841487564
ARIMA(0, 1, 0)x(0, 1, 1, 12) - AIC:270.20449054798723
ARIMA(0, 1, 0)x(1, 1, 0, 12) - AIC:279.7073077170952
ARIMA(0, 1, 0)x(1, 1, 1, 12) - AIC:272.20429383065317
ARIMA(0, 1, 1)x(0, 1, 0, 12) - AIC:248.2004574618413
ARIMA(0, 1, 1)x(0, 1, 1, 12) - AIC:209.46795258585362
ARIMA(0, 1, 1)x(1, 1, 0, 12) - AIC:219.76010995507397
ARIMA(0, 1, 1)x(1, 1, 1, 12) - AIC:213.63266407486356
ARIMA(1, 1, 0)x(0, 1, 0, 12) - AIC:292.5090537220262
ARIMA(1, 1, 0)x(0, 1, 1, 12) - AIC:250.76816771015618
ARIMA(1, 1, 0)x(1, 1, 0, 12) - AIC:251.43830162843227
ARIMA(1, 1, 0)x(1, 1, 1, 12) - AIC:251.1402407735711
ARIMA(1, 1, 1)x(0, 1, 0, 12) - AIC:243.34941237032209
ARIMA(1, 1, 1)x(0, 1, 1, 12) - AIC:206.44248559031112
ARIMA(1, 1, 1)x(1, 1, 0, 12) - AIC:211.64269806160195
ARIMA(1, 1, 1)x(1, 1, 1, 12) - AIC:210.80404367428187
在这里,我们是通过最佳准则函数法来确定具体的参数值的,模型选择的AIC准则越小,我们就大概可以认为该模型越优。通过上述结果我们可以容易得到ARIMA(0, 1, 1)(0, 1, 1,)12模型相对最优。因此我们选择ARIMA(0, 1, 1)(0, 1, 1,)12模型作为我们预测时间序列的最佳模型。
模型预测
我们使用我们选取的最佳模型进行预测。
Python3:
import statsmodels.api as sm
df = pd.DataFrame(dataSet,index=dateSet,columns=['real value']) # 原始时间序列
mod = sm.tsa.statespace.SARIMAX(df,order=(0,1,1),seasonal_order=(1, 1, 1, 12),enforce_stationarity=False,enforce_invertibility=False)
result = mod.fit()
predict_sunspots = result.forecast(12)
forcast = np.array(predict_sunspots[:]).reshape(-1)
print(forcast)
>>>
[19.42912085 17.40614606 21.53290186 22.27891 23.06918964 23.69105707
22.54036142 23.49219397 24.56108863 24.69965562 26.02344756 26.41517033]
模型指标MAPE

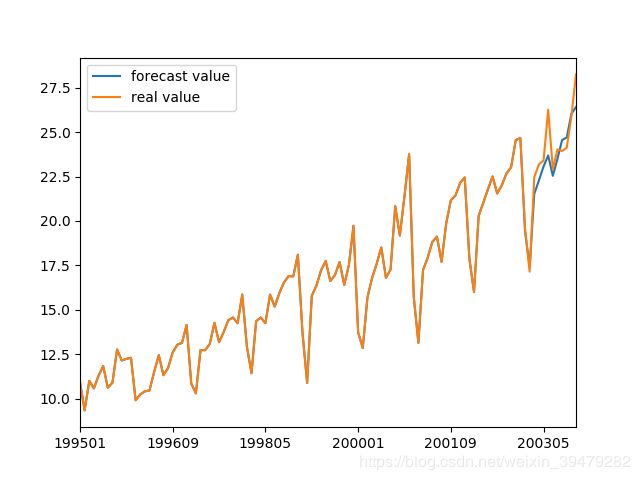
计算预测值和真实值得MAPE指标,得到MAPE指标值为3.14%,通过这个指标我们可以认为该模型是一个好模型。
预测值和真实值趋势对比图
结尾
这是我第一次建立季节性ARIMA模型,如果中间出现错误或者有不合理的地方,还望各位海涵并指正出来,大家一起学习就是要相互纠错,只有这样大家才可以在学习上相互收益、相互进步。同时我也希望这篇文章可以给苦恼于如何用Python建立时间序列模型的朋友指明一条明路。