数学建模（一）

前几周学校搞数学建模，作为一名Python爱好者怎么能袖手旁观，于是跟着两位大佬去混日子（躺是真得爽）。下面分享一下大致过程给大家参考参考，有什么可以优化的希望大家提出来 （这次先分享第一题，后续会更新后面4题）
首先先看一下题目吧

好的，总体来看是一个时间序列的分析建模，感觉还行。我们先来做第一题：数据可视化，感觉挺简单。不就是做一个图表嘛，看怎么做才做得好看而已，描述性分析？哈哈，不就乱吹B嘛！
然而在收集数据的时候我还是太天真了，仔细看，重庆近20年38个区县的人口和经济！！！！我的天啊！！！
经过了一天的收集我们终于收集完了，我们收集了重庆38个区县1997-2018的GDP和人口总数。GDP的部分数据截图（人口的数据就不发了）

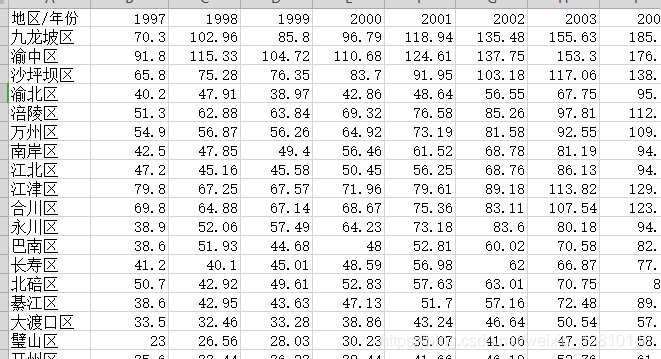
有了数据我们就来做可视化吧，我们是先做了GDP的可视化。因为数据是三维的，所以我们想做三维图来可视化，但是技术和时间有限，所以没有去研究三维图，最终我们决定做成那种柱形图。不解释了，直接上代码和可视化截图：

# coding=UTF-8
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']  #用来显示中文标签
plt.raParams['axes.unicode_minus']=False  #用来正常显示负号

A = [70.3, 91.8, 65.8, 40.2, 51.3, 54.9, 42.5, 47.2, 79.8, 69.8, 38.9, 38.6, 41.2, 50.7, 38.6, 33.5, 23.0, 35.6, 38.9, 30.4, 28.5, 28.3, 23.1, 16.7, 19.2, 22.7, 21.2, 19.3, 17.2, 13.7, 10.2, 10.9, 11.6, 10.8, 10.7, 9.5, 6.6, 3.7]

B = [102.96, 115.33, 75.28, 47.91, 62.88, 56.87, 47.85, 45.16, 67.25, 64.88, 52.06, 51.93, 40.1, 42.92, 42.95, 32.46, 26.56, 33.44, 33.2, 29.2, 29.79, 28.49, 24.43, 20.92, 21.43, 23.14, 20.68, 21.23, 17.18, 17.74, 11.15, 12.05, 12.8, 12.0, 10.93, 11.51, 7.18, 4.08]

C = [85.8, 104.72, 76.35, 38.97, 63.84, 56.26, 49.4, 45.58, 67.57, 67.14, 57.49, 44.68, 45.01, 49.61, 43.63, 33.28, 28.03, 36.23, 36.06, 36.01, 29.8, 29.68, 29.02, 23.2, 21.91, 20.49, 21.25, 21.07, 19.26, 16.38, 11.91, 12.48, 12.73, 12.45, 11.24, 11.32, 7.3, 4.18]

D = [96.79, 110.68, 83.7, 42.86, 69.32, 64.92, 56.46, 50.45, 71.96, 68.67, 64.23, 48.0, 48.59, 52.83, 47.13, 38.86, 30.23, 38.44, 39.66, 40.01, 31.32, 32.05, 32.01, 25.75, 23.58, 22.13, 22.87, 22.61, 20.81, 18.01, 13.98, 13.54, 12.74, 12.13, 12.21, 11.34, 8.1, 4.4]

E = [118.94, 124.61, 91.95, 48.64, 76.58, 73.19, 61.52, 56.25, 79.61, 75.36, 73.18, 52.81, 56.98, 57.63, 51.7, 43.24, 35.07, 41.66, 43.02, 44.77, 34.58, 33.7, 35.42, 29.01, 26.28, 24.28, 24.82, 24.44, 22.93, 20.19, 15.93, 14.8, 14.44, 13.21, 13.45, 12.29, 8.93, 4.9]

F = [135.48, 137.75, 103.18, 56.55, 85.26, 81.58, 68.78, 68.76, 89.18, 83.11, 83.6, 60.02, 62.0, 63.01, 57.16, 46.64, 41.06, 46.19, 48.79, 50.31, 39.21, 37.18, 39.19, 32.92, 31.62, 27.37, 27.77, 27.75, 26.32, 22.77, 18.49, 16.82, 16.39, 14.75, 15.21, 13.31, 9.86, 5.39]

G = [155.63, 153.3, 117.06, 67.75, 97.81, 92.55, 81.19, 86.13, 113.82, 107.54, 80.18, 70.58, 66.87, 70.75, 72.48, 50.54, 47.52, 52.76, 55.71, 55.76, 44.45, 41.58, 45.28, 37.9, 35.49, 30.18, 31.97, 31.55, 29.93, 25.42, 20.82, 19.25, 18.92, 17.0, 17.38, 14.72, 11.07, 6.09]

H = [185.5, 176.2, 138.7, 95.1, 112.9, 109.3, 94.8, 94.9, 129.7, 123.5, 94.1, 82.4, 77.8, 81.0, 89.3, 57.2, 58.1, 61.1, 66.4, 65.2, 52.7, 49.9, 54.2, 44.3, 42.6, 33.9, 38.1, 37.3, 34.0, 28.9, 25.7, 23.3, 23.3, 20.4, 19.3, 17.5, 12.8, 7.9]

I = [270.41, 240.99, 163.17, 145.52, 135.08, 133.44, 114.02, 135.97, 133.29, 130.45, 113.13, 100.87, 87.02, 80.16, 81.16, 70.24, 66.1, 70.48, 67.86, 72.38, 56.5, 58.41, 60.81, 50.92, 48.81, 45.33, 43.87, 43.29, 36.81, 36.54, 29.87, 29.07, 27.41, 25.22, 20.49, 20.12, 14.73, 10.11]

J = [315.23, 243.23, 193.05, 183.11, 153.87, 152.29, 129.8, 151.42, 148.94, 142.16, 126.19, 116.32, 100.05, 91.8, 87.31, 77.25, 75.8, 75.13, 73.26, 71.44, 69.52, 66.1, 63.56, 54.12, 52.4, 50.86, 50.04, 46.68, 39.95, 39.91, 33.55, 30.47, 29.64, 29.02, 22.66, 22.2, 15.95, 11.1]

K = [374.56, 279.5, 299.64, 245.46, 192.27, 190.48, 156.8, 179.79, 175.91, 167.76, 153.03, 142.57, 125.26, 110.22, 103.13, 93.89, 90.51, 91.47, 85.56, 87.61, 80.48, 85.09, 73.33, 66.83, 61.52, 61.98, 61.58, 55.71, 47.97, 49.13, 40.03, 37.61, 39.66, 35.52, 19.62, 27.64, 20.39, 13.78]

L = [431.3, 326.21, 271.18, 301.8, 253.48, 256.06, 225.8, 219.13, 219.24, 203.47, 192.07, 175.56, 143.82, 155.86, 125.21, 142.43, 113.49, 109.0, 101.89, 111.0, 100.49, 110.03, 86.31, 81.56, 75.42, 75.33, 77.8, 66.48, 57.47, 60.48, 49.81, 50.05, 50.04, 43.95, 32.2, 32.92, 23.56, 19.54]

M = [500.03, 468.36, 347.69, 459.4, 355.04, 396.45, 300.15, 325.35, 249.29, 228.75, 244.08, 243.33, 176.38, 192.36, 140.97, 149.56, 128.05, 123.03, 118.63, 127.8, 114.73, 129.98, 95.59, 94.68, 92.52, 85.58, 93.69, 74.61, 65.71, 79.1, 59.2, 58.14, 62.12, 55.18, 41.91, 47.7, 30.94, 20.89]

N = [589.58, 553.03, 419.54, 573.64, 434.49, 500.13, 349.43, 391.39, 303.0, 244.49, 300.04, 308.72, 228.64, 232.37, 167.28, 177.21, 152.76, 149.28, 145.01, 150.18, 143.55, 159.95, 116.79, 113.87, 111.11, 102.97, 109.41, 85.76, 77.12, 100.13, 72.42, 66.39, 75.91, 64.81, 50.31, 58.16, 37.6, 25.01]

O = [690.54, 665.29, 560.25, 767.86, 557.34, 622.59, 434.16, 516.52, 383.85, 306.36, 380.2, 395.1, 317.69, 303.01, 264.41, 149.85, 208.3, 199.76, 233.87, 195.64, 169.85, 207.55, 146.93, 147.48, 131.46, 128.45, 136.87, 109.28, 99.77, 129.19, 86.58, 76.45, 93.49, 80.15, 63.49, 81.09, 47.5, 36.98]

P = [776.3, 766.03, 658.14, 879.32, 630.53, 662.86, 465.56, 527.76, 426.01, 347.54, 402.68, 420.85, 336.41, 334.76, 286.67, 127.08, 252.88, 229.55, 246.71, 226.15, 176.18, 229.81, 162.75, 168.83, 156.65, 114.57, 156.8, 126.63, 111.08, 147.95, 98.4, 85.78, 106.08, 93.1, 70.35, 89.29, 53.11, 40.75]

Q = [823.58, 804.2, 701.28, 1001.76, 690.04, 702.03, 523.03, 554.86, 486.58, 387.42, 432.39, 465.93, 374.08, 371.58, 320.56, 136.62, 301.9, 265.47, 278.33, 255.26, 147.48, 261.03, 190.77, 198.29, 182.66, 160.11, 182.63, 150.34, 119.69, 167.81, 107.91, 97.46, 114.62, 107.43, 75.13, 100.25, 60.22, 42.6]

R = [910.82, 868.72, 809.21, 1115.38, 757.48, 771.22, 608.14, 604.46, 554.66, 440.46, 512.54, 510.08, 420.41, 415.41, 357.99, 148.97, 334.38, 300.17, 329.84, 281.05, 173.19, 300.42, 234.16, 224.09, 217.83, 181.41, 208.26, 170.19, 135.37, 186.31, 119.98, 108.8, 126.5, 119.95, 81.27, 110.42, 66.72, 46.0]

S = [1003.57, 958.17, 714.3, 1193.34, 813.19, 828.22, 679.38, 687.31, 605.59, 476.19, 570.34, 568.34, 430.12, 430.34, 378.04, 159.72, 381.76, 325.98, 349.17, 308.2, 186.25, 329.87, 265.2, 239.84, 242.33, 197.43, 222.4, 187.91, 150.19, 202.55, 131.4, 115.97, 138.19, 129.24, 89.66, 116.97, 73.4, 49.1]

T = [1089.67, 1050.21, 785.97, 1293.35, 896.22, 897.39, 745.5, 778.01, 674.12, 532.19, 636.18, 635.35, 454.02, 475.41, 420.14, 176.66, 428.35, 360.62, 386.59, 341.57, 210.78, 368.12, 300.65, 263.31, 271.02, 222.57, 240.7, 213.11, 170.56, 218.84, 145.61, 128.69, 150.62, 145.42, 101.79, 129.48, 82.37, 45.12]

U = [1130.0, 1122.0, 860.0, 1447.0, 992.0, 966.0, 792.0, 880.0, 757.0, 580.0, 705.0, 709.0, 510.0, 530.0, 467.0, 197.0, 480.0, 400.0, 430.0, 382.0, 233.0, 415.0, 334.0, 277.0, 298.0, 251.0, 271.0, 230.0, 187.0, 232.0, 160.0, 141.0, 167.0, 162.0, 112.0, 142.0, 88.0, 49.0]

V = [1211.25, 1203.85, 936.41, 1543.09, 1076.13, 982.58, 724.78, 1027.87, 902.33, 712.93, 845.67, 781.22, 597.49, 551.79, 555.63, 228.13, 527.3, 473.13, 517.65, 456.98, 280.37, 504.88, 308.95, 316.95, 331.26, 300.68, 307.95, 275.05, 234.96, 247.29, 181.63, 170.11, 185.64, 175.97, 142.64, 157.96, 103.73, 55.78]

x = np.arange(38) #总共有38个区县,所以我们设置为38个
total_width, n = 0.8, 22    #总共是22年，所以我们设置为22,  0.8是柱状图的柱宽
width = total_width / n
x = x - (total_width - width) / 2

plt.bar(x, A, color = "r",width=width,label='1997 ')
plt.bar(x + width, B, color = "y",width=width,label='1998')
plt.bar(x + 2 * width, C , color = "c",width=width,label='1999')
plt.bar(x + 3 * width, D , color = "g",width=width,label='2000')
plt.bar(x + 4 * width, E, color = "r",width=width,label='2001')
plt.bar(x + 5 * width,F, color = "y",width=width,label='2002')
plt.bar(x + 6 * width, G , color = "c",width=width,label='2003')
plt.bar(x + 7 * width, H , color = "g",width=width,label='2004')
plt.bar(x + 8 * width, I, color = "r",width=width,label='2005')
plt.bar(x + 9 * width, J, color = "y",width=width,label='2006')
plt.bar(x + 10 * width, K , color = "c",width=width,label='2007')
plt.bar(x + 11 * width, L , color = "g",width=width,label='2008')
plt.bar(x + 12 * width, M, color = "r",width=width,label='2009')
plt.bar(x + 13 * width, N, color = "y",width=width,label='2010')
plt.bar(x + 14 * width, O , color = "c",width=width,label='2011')
plt.bar(x + 15 * width, P , color = "g",width=width,label='2012')
plt.bar(x + 16 * width, Q, color = "r",width=width,label='2013')
plt.bar(x + 17 * width, R, color = "y",width=width,label='2014')
plt.bar(x + 18 * width, S , color = "c",width=width,label='2015')
plt.bar(x + 19 * width, T , color = "g",width=width,label='2016')
plt.bar(x + 20 * width, U , color = "c",width=width,label='2017')
plt.bar(x + 21 * width, V , color = "g",width=width,label='2018')

plt.xlabel("城市")
plt.ylabel("GDP(亿元)")
plt.legend(loc = "best")
plt.xticks([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37],['九龙坡', '渝中', '沙坪坝', '渝北', '涪陵', '万州', '南岸', '江北', '江津', '合川', ' 永川', '巴南', '长寿', '北碚', '綦江', '大渡口', '璧山', '开州', '大足', '铜梁', '南川', '荣昌', '潼南', '垫江', '梁平', '奉节', '忠县', '云阳', '丰都', '黔江', '武隆', '彭水', '秀山', '石柱', '巫山', '酉阳', '巫溪', '城口'])

my_y_ticks = np.arange(3, 1600, 100)#分别代表：设置图表Y轴的最小值,最大值,数值间隔

plt.ylim((3, 1600))#Y轴的最小值和最大值
plt.yticks(my_y_ticks)
plt.show()

代码效果如下：

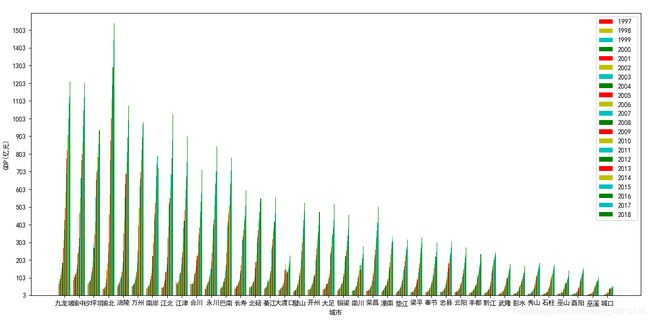
是不是看着很眼花，其实我写论文的时候是先上了38个区县的GDP近20年的GDP的可视化图。但是后面我将重庆分成4个部分来分别做可视化，这个可以通过修改代码来实现。

下面再给出人口数据可视化的截图（将上面的代码修改一下就OK了）。

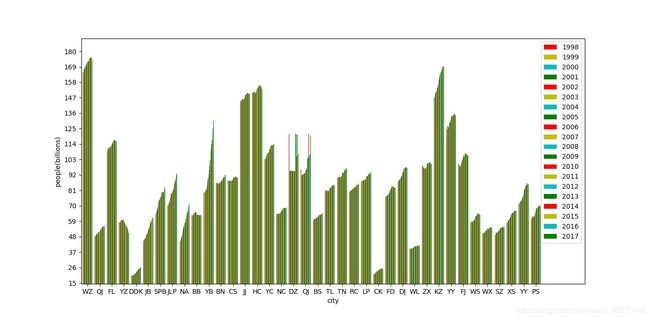
各区县用拼音首字母代替了，其实大家可以对号入座一下，比如YB（渝北），人口和经济都有一定的对应关系。然后大家就可以进行描述性分析了（chui bi）。很简单吧，那么第一题的大致过程就是这样。

最后给大家推荐一个不错的Python库——pycharts。这个库就是用来做图表的，能做三维图，热力图等等，而且图表观赏性高，通俗易懂。大家可以学习一下拿来做数据可视化还是不错滴。
噢对了，可视化代码参考于这个博客https://blog.csdn.net/u012328159/article/details/79240652。谢谢这位大佬，大家如果对怎么修改代码有疑问的话，可以打开上面这个博客配合图片代码注释来理解这个代码的含义。

需要数据的去我的资源那里找一下（因为还在审核），由于数据是我们3个人辛辛苦苦收集整理的，想赚点辛苦分，希望大家见谅。