图论——最大流的增广路相关算法(基于Ford–Fulkerson方法的DFS和BFS、Dinic算法)
文章目录
- 最小割定理
- 基于Ford–Fulkerson方法的DFS
- Ford-Fulkerson方法的BFS实现:Edmond-Karp算法
- Dinic算法、弧优化
- 后记
最小割定理
割( C U T CUT CUT),指对于某个顶点集合 S S S包含于集合 V V V,从 S S S出发指向 T T T的那些边的集合,记为 C U T ( S , T ) CUT(S,T) CUT(S,T),这些边的容量之和称为割的容量。设 s s s属于集合 S S S, t t t属于集合 V − S V-S V−S,如果将网络中 s s s- t t t割所包含的边都删去,就不存在 s s s指向 t t t的路径了。
f f f为流, C U T ( s , t ) CUT(s,t) CUT(s,t)为任意的割, f f f的值为所有正向割边的流量与负向割边的差。因为有 f f f的流量等于 s s s出边的总流量,对于任意的非 s s s点 v v v, v v v的出边总流量等于它的入边总流量,所以 f f f的流量等于出 s s s所有结点的出边总流量减入边总流量。由此可知,如果 f f f是网络中的一个流, C U T ( s , t ) CUT(s,t) CUT(s,t)是一个割,那么f的值不超过割 C U T ( s , t ) CUT(s,t) CUT(s,t)的容量。网络中的最大流不超过任何割的容量。
在网络中,如果f是一个流,CUT (S,T)是一个割,且f的值等于割CUT(S,T)的容量,那么f是一个最大流, CUT(S,T)是一个最小割。
增广路相关算法的目的就是使得源点到汇点的割所包含的边全部删去。当源点到汇点无路可走时,则 f f f到达最大值。
基于Ford–Fulkerson方法的DFS
Ford-Fulkerson方法的一种实现是利用DFS寻找增广路径和删去 “ 割集中的边 ”。每次找到一条从源点到汇点的路径,记录这条路径的流的最大值即为路径上权值最小的边。并建立反边表示 “ 删去” 正向边,以便于在后来调整路径。当没有通向汇点的路径时,流饱和,退出搜索。由于每次DFS至少找到一条流 f = 1 f=1 f=1的路径,并且最多遍历所有边,所以该算法的复杂度 O ( f ∣ E ∣ ) O(f|E|) O(f∣E∣),不过这种最差的情况一般是不会出现的,总体上说该算法还是比较快的。(除非出题者坑你)
为了便于理解,我用一些图表现这一算法的思路。
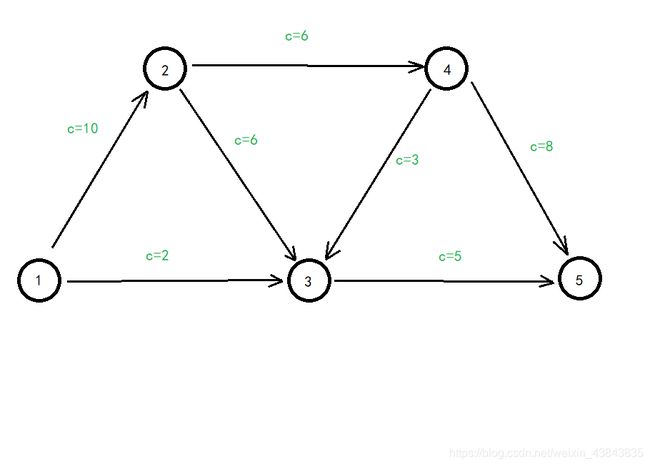
设 c c c为路的容量, r r r为反向边的容量, f f f为占用的流。
建立一张图,假设此时求点1到点5的最大流。
#include
}
cout<<flow<<endl;
return 0;
}
Ford-Fulkerson方法的BFS实现:Edmond-Karp算法
Edmond-Karp是FF方法的BFS实现方式,其稳定性高于上面用DFS找增广路的方法,不会因为最大流的限制而出现爆炸性的时间消耗,其时间复杂度为 O ( V E 2 ) O(VE^2) O(VE2)。
思想同Ford-Fulkerson方法,代码已经注释;
#includeDinic算法、弧优化
算法原理
DInic算法是对Edmond-Karp算法的一种优化,它总是寻找最短的增广路径(通过结点数少),并沿着这条路径更新流。最短增广路径的长度在增广过程中始终不会变短,所以无需每次找增广路前都进行一次bfs。可以先进行一次bfs,按各个点被发现的顺序建立分层图,然后我们在进行dfs找到最短的增广路径,即增广的方向就是先被发现点指向后被发现的点。当没有新的最短增广路径时,意味着需要扩大最短增广路径的长度。此时再进行一次bfs,顺便可以检测是否还有通向汇点的路径。每一次bfs建立分层图的时间复杂度都是 O ( E ) O(E) O(E),每一步最短增广路径的长度至少增加 1 1 1,最多增加到 ∣ V ∣ − 1 |V|-1 ∣V∣−1。时间复杂度最坏为 O ( ∣ E ∣ ∣ V ∣ 2 ) O(|E||V|^2) O(∣E∣∣V∣2).实际操作中很难出现能卡死该算法的反人类图。
弧优化
我们用邻接表建图,对于一次bfs预处理下的dfs搜索最短增广路操作,实际上是重复利用残余图。但是没有必要对一个结点已经搜索过的边重复搜索,因此用一个数组,记录此时应该从这个结点的第几条边开始遍历。
#include后记
由于博主太菜了,本来是要弄几道例题做做的,奈何找到的例题都是神仙题。凭我的菜鸡水平完全看不出是网络流题。。。
所以没有例题了。。。