数位DP专题

CF55D

这个题的核心要素是：某个数n被它的所有非零数位整除的同时，也是整除了所有非零数位的最小公倍数。所以在分析数位的同时需要照顾已经分析的所有非零数位的最小公倍数，和这些数位组成的这个数取余它的模。

所以dfs过程就有了三维数据：当前数位，余数，最小公倍数。然而余数和最小公倍数可能很大，在记忆化过程中较难实现，所以需要优化一下。可以发现1~9的最小公倍数为2520，如果一个数被2520整除，那么就可以断定无论如何都可以被它的每一位整除。但是数位的所有数字并不全是1~9，还可能有别的数字，所以只要取余数位最小公倍数为0的都可以认为满足条件。

至此，空间可以优化到20*2520*2520，但是这样仍然会空间超限。可以发现最后一维，也就是最小公倍数只有48种组成情况（因式分解），所以可以把它压成48个大小，再利用一个哈希数组使1~48各自都对应一个因数组成方案。

//#include
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
//#define endl '\n'
#define DETERMINATION main
#define For(a,b,c,d) for(int a=b;a<=c;a+=d)
#pragma GCC optimize(2)
#pragma warning(disable:4996)
#define lldin(a) scanf("%lld", &a)
#define println(a) printf("%lld\n", a)
#define print(a) printf("%lld ", a)
#define reset(a, b) memset(a, b, sizeof(a))
#define debug std::cout<<"procedures above are available"<<"\n";
#define BigInteger __int128
using namespace std;
const long long INF = 2147483647;
const double PI = acos(-1);
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int mod = 1e9 + 7;
//template
//inline BigInteger nextBigInteger()
//{
//    BigInteger tmp = 0, si = 1;char c;    c = getchar();
//    while (!isdigit(c))
//{if (c == '-')si = -1;c = getchar();}
//    while (isdigit(c))
//    {tmp = tmp * 10 + c - '0';c = getchar();}
//    return si * tmp;
//}
//std::ostream& operator<<(std::ostream& os, __int128 T)
//{
//    if (T<0) os<<"-";if (T>=10 ) os<0 ? (int) (T%10) : -(int) (T%10) ) ;
//}
//void output(BigInteger x)
//{
//    if (x < 0)
//    {x = -x;putchar('-');}
//    if (x > 9) output(x / 10);
//    putchar(x % 10 + '0');
//    }
/**Operation Overlord 1944.6.6 Daybreak**/
/**Last Remote**/
ll dp[50][2530][50];
ll digits[500],pts=0;
mapmp;
namespace DigitsDp
{
	void preparation()
	{
		pts = 0;
		reset(digits, 0);
	}
	void div(ll x)
	{
		while (x)
		{
			digits[++pts] = x % 10;
			x /= 10;
		}
	}
	void getFactors()
	{
		ll cnt = 0;
		for (int i = 1; i <=2520; i++)
		{
			if (2520 % i == 0)
				mp[i] = ++cnt;
		}
	}
	ll gcd(ll a, ll b)
	{
		return b == 0 ? a : gcd(b, a%b);
	}
	ll Lcm(ll a, ll b)
	{
		return a * b / gcd(a, b);
	}
	ll dfs(ll current, ll mod, ll lcm, bool boundary)
	{
		if (current == 0)
		{
			//cout << current << " " << mod << " " << lcm << " " << boundary << endl;
			return mod % lcm == 0 ? 1 : 0;
		}
		if (boundary==false&&dp[current][mod][mp[lcm]]!=-1)
			return dp[current][mod][mp[lcm]];
		else
		{
			//cout << current << " " << mod << " " << lcm << " "<> t;
	reset(dp, -1);
	mp.clear();
	DigitsDp::getFactors();
	for (int j = 1; j <= t; j++)
	{
		ll lower, upper;
		cin >> lower >> upper;
		DigitsDp::preparation();
		DigitsDp::div(upper);
		ll ans1=DigitsDp::dfs(pts, 0, 1, true);
		DigitsDp::preparation();
		DigitsDp::div(lower-1);
		ll ans2 = DigitsDp::dfs(pts, 0, 1, true);
		cout << ans1 - ans2 << endl;
	}
	return 0;
}

HDU4352

本题意思是求出单个数内的数位即构成K个长度的LIS的数的个数。如果要求出这么个LIS，绕不开那两种求LIS的办法：动态规划或者贪心+二分，在这里使用的是基于后者思想的变种方法。

因为这是一个根据数位来讨论LIS的题目，单纯利用数组来标记LIS是行不通的，所以就有一种方法来快速标记现在已经形成的LIS，也就是使用01字符串来标记这个LIS，比如说167，就可以表示为0100001100，即长度为3的LIS:1,6,7.

更新LIS的方法自然是从当前位x开始，找到第一个比它大的位，然后替换它。比如说1675的LIS由167变为157，相应的01串也要有这样的变更，除去01串内的一个1可以直接使用异或，相应的添加一个1可直接使用按位或。

值得注意的是本题的时间复杂度不允许T次初始化，所以需要在DP数组内再加一维K，来实现对多种K进行答案储存的功能。

//#include
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
//#define endl '\n'
#define DETERMINATION main
#define For(a,b,c,d) for(int a=b;a<=c;a+=d)
#pragma GCC optimize(2)
#pragma warning(disable:4996)
#define lldin(a) scanf("%lld", &a)
#define println(a) printf("%lld\n", a)
#define print(a) printf("%lld ", a)
#define reset(a, b) memset(a, b, sizeof(a))
#define debug std::cout<<"procedures above are available"<<"\n";
#define BigInteger __int128
using namespace std;
const long long INF = 2147483647;
const double PI = acos(-1);
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int mod = 1e9 + 7;
//template
//inline BigInteger nextBigInteger()
//{
//    BigInteger tmp = 0, si = 1;char c;    c = getchar();
//    while (!isdigit(c))
//{if (c == '-')si = -1;c = getchar();}
//    while (isdigit(c))
//    {tmp = tmp * 10 + c - '0';c = getchar();}
//    return si * tmp;
//}
//std::ostream& operator<<(std::ostream& os, __int128 T)
//{
//    if (T<0) os<<"-";if (T>=10 ) os<0 ? (int) (T%10) : -(int) (T%10) ) ;
//}
//void output(BigInteger x)
//{
//    if (x < 0)
//    {x = -x;putchar('-');}
//    if (x > 9) output(x / 10);
//    putchar(x % 10 + '0');
//    }
/**Operation Overlord 1944.6.6 Daybreak**/
/**Last Remote**/
ll dp[20][1 << 11][12],digits[599];
ll cnt = 0;
namespace solution
{
	void division(ll x)
	{
		cnt = 0;
		while (x > 0)
		{
			digits[++cnt] = x % 10;
			x /= 10;
		}
	}
	ll CheckAns(ll x)
	{
		bitset<23>bt(x);
		return bt.count();
	}
	ll UpdateLIS(ll Original, ll CurrentPos)
	{
		for (int i = CurrentPos; i <= 9; i++)
		{
			if ((Original&(1 << i)) > 0)
				return (Original ^ (1 << i)) | 1 << CurrentPos;
		}
		return Original | 1 << CurrentPos;
	}
	ll dfs(ll current, ll LIS, bool LeadingZeroes, bool Bound,ll request)
	{
		if (current == 0)
		{
			if (CheckAns(LIS) == request)
				return 1;
			else
				return 0;
		}
		if (Bound == false && dp[current][LIS][request] != -1)
			return dp[current][LIS][request];
		else
		{
			ll ans = 0;
			ll limit = Bound == true ? digits[current] : 9;
			for (int i = 0; i <= limit; i++)
			{
				ll nextLIS = (LeadingZeroes&&i == 0) ? 0 : UpdateLIS(LIS, i);
				ans += dfs(current - 1, nextLIS,LeadingZeroes&&i==0,Bound&& i == limit, request);
			}
			if (!Bound)
				dp[current][LIS][request] = ans;
			return ans;
		}
	}
}
int DETERMINATION()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(0), std::cout.tie(0);
	ll t;
	cin >> t;
	reset(dp, -1);
	for (int y = 1; y <= t; y++)
	{
		ll lower, upper, length;
		cin >> lower >> upper >> length;
		cout << "Case #" << y << ": ";
		solution::division(lower-1);
		ll ans1 = solution::dfs(cnt, 0, true, true, length);
		solution::division(upper);
		ll ans2 = solution::dfs(cnt, 0, true,true, length);
		cout << ans2 - ans1 << endl;
	}
	return 0;
}

POJ3252

数位DP模板题，但是新颖的地方在于这是对一个十进制数字的二进制表达式进行分析，相应的，只要把数字拆分成二进制形式就可以解决这个问题。

HDU3709

对数字的平衡点进行枚举，然后依据当前平衡点利用数位DP进行分析即可。值得一说的是在数位DP中会出现00000这种数字，这是因为dfs的过程中多次选择了0，造出了这么一个情况，实际上只有0需要被统计，00，000等都是完全多余的。这样的可以使用判断前导零的方式消除它的影响，或者直接在答案出减去（n-1）即可。这是因为对于n位数，0,00,000...00（n个0）有n个，被重复计算的有n-1个。

//#include
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
//#define endl '\n'
#define DETERMINATION main
#define For(a,b,c,d) for(int a=b;a<=c;a+=d)
#pragma GCC optimize(2)
#pragma warning(disable:4996)
#define lldin(a) scanf("%lld", &a)
#define println(a) printf("%lld\n", a)
#define print(a) printf("%lld ", a)
#define reset(a, b) memset(a, b, sizeof(a))
#define debug std::cout<<"procedures above are available"<<"\n";
#define BigInteger __int128
using namespace std;
const long long INF = 2147483647;
const double PI = acos(-1);
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int mod = 1e9 + 7;
//template
//inline BigInteger nextBigInteger()
//{
//    BigInteger tmp = 0, si = 1;char c;    c = getchar();
//    while (!isdigit(c))
//{if (c == '-')si = -1;c = getchar();}
//    while (isdigit(c))
//    {tmp = tmp * 10 + c - '0';c = getchar();}
//    return si * tmp;
//}
//std::ostream& operator<<(std::ostream& os, __int128 T)
//{
//    if (T<0) os<<"-";if (T>=10 ) os<0 ? (int) (T%10) : -(int) (T%10) ) ;
//}
//void output(BigInteger x)
//{
//    if (x < 0)
//    {x = -x;putchar('-');}
//    if (x > 9) output(x / 10);
//    putchar(x % 10 + '0');
//    }
/**Operation Overlord 1944.6.6 Daybreak**/
/**Last Remote**/
ll dp[50][50][2550];
ll digits[50],cnt;
namespace solution
{
	void division(ll x)
	{
		cnt = 0;
		while (x > 0)
		{
			digits[++cnt] = x % 10;
			x /= 10;
		}
	}
	ll dfs(ll current, ll pivot,ll SideSum,bool bound)
	{
		if (current == 0)
		{
			if (SideSum == 0)
				return 1;
			else
				return 0;
		}
		if (!bound&&dp[current][pivot][SideSum] != -1)
			return dp[current][pivot][SideSum];
		else
		{
			ll ans = 0;
			ll limit = bound == true ? digits[current] : 9;
			for (int i = 0; i <= limit; i++)
			{
				ll nextSum = ((SideSum + (pivot - current)*i));
				ans += dfs(current-1, pivot, nextSum, bound&&i == limit);
			}
			if (!bound)
				dp[current][pivot][SideSum] = ans;
			return ans;
		}	
	}
	ll ReturnAns()
	{
		ll ans = 0;
		for (int i = 1; i <= cnt; i++)
			ans += dfs(cnt, i, 0, true);
		return ans-cnt+1;
	}
}
int DETERMINATION()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(0), std::cout.tie(0);
	ll t;
	cin >> t;
	for (int y = 1; y <= t; y++)
	{
		ll lower, upper;
		cin >> lower >> upper;
		ll ans1, ans2;
		reset(dp, -1);
		solution::division(upper);
		ans1 = solution::ReturnAns();
		reset(dp, -1);
		if (lower == 0)
			ans2 = 0;
		else
		{
			solution::division(lower - 1);
			ans2 = solution::ReturnAns();
		}
		//cout << ans1 << " " << ans2 << endl;
		cout << ans1 - ans2 << endl;
	}
	return 0;
}

HDU4507

本题的主要难点是求平方和。

一般来说，知道一个数字求平方和是很简单的，但是知道一个当前数位就不是那么简单了。这需要如下两个公式：

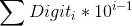$\sum Digit_{i}*10^{i-1}$ （从后往前计算）

$(a+b+c)^{2}=(a+(b+c))^{2}=(a^{2}+2a(b+c)+(b+c)^{2})$

合并起来就是： $(\sum 10^{i-1}D_{i})^{2}+2(\sum10^{i-1}D_{i})(\sum\sum10^{j-1}D_{j})+(\sum\sum10^{j-1}D_{j})^{2}$

可以看出，要求解一个状态的平方和，就需要有两个变量记录一次方和，平方和。但是这两个变量还不够，因为对于每一个状态而言，例如第i个数位（从前往后），它的数据代表着i+1，i+2...Length的状态和。什么意思呢？假如我们用数位DP去求1~20的和，那么对于第2位来说，它的和就是这一位本身（0~9），但是对于第一位来说，它在求和的时候需要考虑在这个数位的下位有多少个数字，即对于1~20而言：0的下位有9个数字（0~9），1的下位有10个数字（10~19），2的下位有1个数字（0）,在求和的时候就需要再乘下位数字的个数，即（0*10*9+45)+(1*10*10+45)+(2*10+0)=210,45在这里的是个位数和。

所以还需要第三个变量来记录下位数字个数。

对于数位DP中的每位数来说，就会有如下的操作：

	ans.cnt += tmp.cnt%mod;
					ans.cnt %= mod;
					ans.sum += (power[current - 1]%mod * i%mod*tmp.cnt%mod + tmp.sum%mod)%mod;
					//cout << "ans.sum: " << power[current - 1] << " " << i << " " << tmp.cnt << endl;
					ans.sum %= mod;
					ans.sqrtsum += (tmp.sqrtsum%mod + 2 * i%mod*power[current - 1] % mod* tmp.sum%mod)%mod;
					ans.sqrtsum %= mod;
					ans.sqrtsum += (tmp.cnt%mod*i%mod*i%mod*power[current - 1]%mod * power[current - 1] % mod)%mod;
					ans.sqrtsum %= mod;

先更新当前位的下位数字数。
然后更新当前位所得到的总和。
最后更新平方和（注意，这里是回溯，所以对于公式 $(a+b+c)^{2}=(a+(b+c))^{2}=(a^{2}+2a(b+c)+(b+c)^{2})$ ，在这里是已知了(b+c)的平方和以及一次方和，来求原式的值）。

（由于每个数都可能很大，建议多次取模或者用防溢出乘法重载运算符）

//#include
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
//#define endl '\n'
#define DETERMINATION main
#define For(a,b,c,d) for(int a=b;a<=c;a+=d)
#pragma GCC optimize(2)
#pragma warning(disable:4996)
#define lldin(a) scanf("%lld", &a)
#define println(a) printf("%lld\n", a)
#define print(a) printf("%lld ", a)
#define reset(a, b) memset(a, b, sizeof(a))
#define debug std::cout<<"procedures above are available"<<"\n";
#define BigInteger __int128
using namespace std;
const long long INF = 2147483647;
const double PI = acos(-1);
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int mod = 1e9 + 7;
//template
//inline BigInteger nextBigInteger()
//{
//    BigInteger tmp = 0, si = 1;char c;    c = getchar();
//    while (!isdigit(c))
//{if (c == '-')si = -1;c = getchar();}
//    while (isdigit(c))
//    {tmp = tmp * 10 + c - '0';c = getchar();}
//    return si * tmp;
//}
//std::ostream& operator<<(std::ostream& os, __int128 T)
//{
//    if (T<0) os<<"-";if (T>=10 ) os<0 ? (int) (T%10) : -(int) (T%10) ) ;
//}
//void output(BigInteger x)
//{
//    if (x < 0)
//    {x = -x;putchar('-');}
//    if (x > 9) output(x / 10);
//    putchar(x % 10 + '0');
//    }
/**Operation Overlord 1944.6.6 Daybreak**/
/**Last Remote**/
struct node
{
	ll cnt, sum, sqrtsum;
}dp[30][30][30];
ll digits[59], cnt2 = 0;
ll power[123];
namespace solution
{
	void division(ll x)
	{
		cnt2 = 0;
		while (x > 0)
		{
			digits[++cnt2] = x % 10;
			x /= 10;
		}
	}
	node dfs(ll current, ll digitMod, ll numberMod, bool bound)
	{
		if (current == 0)
		{
			node tmpans = { 0,0,0 };
			if (digitMod == 0 || numberMod == 0)
				tmpans.cnt = 0;
			else
				tmpans.cnt = 1;
			tmpans.sum = tmpans.sqrtsum = 0;
			return tmpans;
		}
		if (!bound&&dp[current][digitMod][numberMod].cnt != -1)
			return dp[current][digitMod][numberMod];
		else
		{
			node ans = { 0,0,0 };
			ll limit = bound == true ? digits[current] : 9;
			//cout << "power :" << power[current-1] <<" "<> t;
	for (int y = 1; y <= t; y++)
	{
		ll lower, upper;
		cin >> lower >> upper;
		solution::division(upper);
		ll ans1 = solution::dfs(cnt2, 0, 0, true).sqrtsum;
		solution::division(lower - 1);
		ll ans2 = solution::dfs(cnt2, 0, 0, true).sqrtsum;
		//cout << ans1 << " " << ans2 << endl;
		cout << ((ans1 - ans2) % mod + mod) % mod << endl;
	}
	return 0;
}

粉尘识别数据集——工地/矿下粉尘数据识别，数据集已划分，YOLO格式-有权重，相关指数，map相当高毕设宇航 YOLO 机器学习目标跟踪
数据集名称粉尘识别数据集数据集描述这是一个专门针对工地或矿下粉尘识别设计的数据集，包含了大量的高清图像，用于识别施工或采矿环境中产生的粉尘。数据集已经按照标准的数据划分方法分为训练集、验证集和测试集，并且以YOLO格式进行了标注。此外，数据集中还包含了预训练的模型权重和相关性能指标，如mAP（MeanAveragePrecision），表明模型在粉尘识别任务上的表现优异。数据集特点高清图像：所有图
Tensorflow中Keras搭建神经网络六步法及参数详解 -- Tensorflow自学笔记12 青瓷看世界 tensorflow 笔记人工智能深度学习神经网络
一.tf.keras搭建神经网络六步法1.import相关模块如importtensorflowastf。2.指定输入网络的训练集和测试集如指定训练集的输入x_train和标签y_train，测试集的输入x_test和标签y_test。3.逐层搭建网络结构model=tf.keras.models.Sequential()。4.在model.compile()中配置训练方法选择训练时使用的优化器、
fastText 情感分类 dreampai
情感分类任务就是看一段文本，然后分辨这个人是否喜欢他们在讨论的这个东西。情感分类一个最大的挑战就是可能标记的训练集没有那么多，但是有了词嵌入，即使只有中等大小的标记的训练集，你也能构建一个不错的情感分类器image.pngimage.png假设有一个句子：“这个衣服质量不错”通过分词、去除停用词等预处理操作，得到“衣服/质量/不错”获取“衣服”、“质量”、“不错”的对应词向量（可以通过TF-IDF
【机器学习】K近邻可口的冰可乐机器学习机器学习人工智能
2.K近邻K近邻算法（KNN）的基本思想是通过计算待分类样本与训练集中所有样本之间的距离，选取距离最近的K个样本，根据这些样本的标签进行分类或回归。KNN属于非参数学习算法，因为它不假设数据的分布形式，主要依赖距离度量来进行决策。优点简单易懂：KNN算法非常直观，容易理解和实现。无假设：KNN算法对数据没有假设，适用于复杂分布的数据集。适用于多类分类问题：KNN能够处理多类分类问题，只需在投票过程
Spark入门：KMeans聚类算法 17111_Chaochao1984a 算法 spark kmeans
聚类（Clustering）是机器学习中一类重要的方法。其主要思想使用样本的不同特征属性，根据某一给定的相似度度量方式（如欧式距离）找到相似的样本，并根据距离将样本划分成不同的组。聚类属于典型的无监督学习（UnsupervisedLearning）方法。与监督学习（如分类器）相比1，无监督学习的训练集没有人为标注的结果。在非监督式学习中，数据并不被特别标识，学习模型是为了推断出数据的一些内在结构。
YOLOv8模型参数详解 AdaCoding YOLOv8改进系列 YOLO 目标检测
YOLOv8模型参数详解task：任务类型，通常为detect（检测）。mode：模式，train表示训练模式。model：模型配置文件的路径，指定了YOLOv8模型的结构。data：数据集配置文件的路径，包含了训练集和验证集的信息。epochs：训练的轮数。patience：早期停止的耐心值，表示在没有进一步改进后多少轮后停止训练。batch：批处理大小，即每次前向和后向传播使用的样本数。img
【机器学习】任务二：波士顿房价的数据与鸢尾花数据分析及可视化 FHYAAAX 机器学习机器学习数据分析人工智能
目录1.实验知识准备1.1NumPy1.2Matplotlib库1.3scikit-learn库：1.4TensorFlow1.5Keras2.波士顿房价的数据分析及可视化2.1波士顿房价的数据分析2.1.1步骤一：导入所需的模块和包2.1.2步骤二：从Keras库中加载波士顿房价数据集2.1.3步骤三：加载本地CSV数据集2.1.4步骤四：划分特征和目标变量2.1.5步骤五：划分训练集和测试集2
Zero-Shot Image Classification总结夏日小光
1任务说明现有的benchmark通过ImageNet-1k上预训练的Res101从已知类的训练集提取feature或者featuremap，然后对每一个类引入一个语义标签，可能是属性标签（attributelabel）、或者描述标签（sentenceembedding）等。对于某个类的属性标签（向量形式），每个维度表示一种属性，该维度下的取值表示这个属性在该类别中存在的可能性，值得注意的是ben
训练过程训练集的准确率都低于验证集和测试集的准确率可能的原因 Wils0nEdwards python 人工智能深度学习
每一个epoch训练集的准确率都低于验证集和测试集的准确率，这种现象不太常见，可能有以下几个原因：1.数据增强过强如果你在训练集上使用了较强的数据增强（如随机翻转、ColorJitter等），而验证集和测试集仅进行了基础的预处理。这会导致训练集的样本更具挑战性，模型在训练集上的表现不如在验证集和测试集上的表现。2.训练和验证集分布差异训练集、验证集和测试集的分布可能存在差异。如果训练集包含更多的噪
识别实验笔记和经验总结 Wils0nEdwards 笔记
1.跑对比实验之前，首先保证对比的公平性和可靠性！在进行图像分类模型对比实验时，为了确保对比的公平性和可靠性，以下几个因素需要重点考虑：数据集的一致性：数据集分割：确保训练集、验证集和测试集的划分是一致的。各模型使用相同的训练数据和测试数据。数据集大小：确保数据集的样本数量充足且具有代表性，避免数据集过小导致结果不具备普遍性。数据预处理：图像预处理方法：所有模型使用相同的预处理方法（如归一化、裁剪
遥感影像-语义分割数据集：GID数据集详细介绍及训练样本处理流程 GIS潮流计算机视觉人工智能机器学习
GID数据集：大规模高分卫星土地覆盖数据集原始数据集详情简介：GID是基于我国Gaofen-2卫星数据而构建的大规模高分辨率遥感图像土地覆盖数据集。GID数据集分为大规模分类集（GID-5）和精细土地覆盖集（GID-15）两个部分。大规模分类集（GID-5）包含建筑、农田、森林、草地和水域等5个土地覆盖类别，共计150景像素级标注的Gaofen-2卫星遥感图像。其中，训练集为120景图像，验证集为
Datawhale x李宏毅苹果书入门 AI夏令营 task03学习笔记 weixin_75033552 人工智能学习笔记
实践方法论训练模型的基本步骤：（如下图所示）用训练集训练模型，（最终得出来最优的参数集）将最优参数集带入模型中，用测试集测试模型（人话：将最优参数集带入原来函数中，用测试集的x值计算y值）（这个过程就叫做预测）训练过程中遇到问题的解决攻略（看下图的方式是“前序遍历”）modelbias出现问题的情况：1.看trainingdata的loss，太大；2.当你模型无论如何调整参数，训练的结果还是不够好
机器学习（2）单变量线性回归天凉玩个锤子
2.1模型表示我们学习的第一个算法是线性回归算法。在监督学习中，我们有一个数据集，这个数据集被称为训练集（TrainingSet）。我们用小写字母m来表示训练样本的数目。监督学习算法的工作方式以房屋价格的训练为例，将训练集里房屋价格喂给学习算法，学习算法工作后输出一个函数h，h代表hypothesis（假设）。函数h输入为房屋尺寸大小x，h根据输入来得出y值，y值对应房子的价格。因此，h是一个从x
工地工程车分类检测数据集 6300张带标注 voc yol 计算机视觉从业者数据集分类人工智能机器学习工地工程车汽车
数据集特点类型：工地工程车分类检测数据集。格式：VOC和YOLO格式，适用于训练目标检测模型。规模：共包含6300张图像。标注：使用.xml（VOC格式）和.txt（YOLO格式）文件进行标注，每个文件对应一张图像，标注格式分别为VOC和YOLO格式。类别：包含多种工地工程车辆类别。质量：数据集标注准确，涵盖了多种工地环境下的工程车辆。数据集组成训练集：用于训练模型，包含约5000张图像。验证集：
sklearn 评估模型常用函数小Z资本 sklearn 人工智能 python
`sklearn.metrics`是scikit-learn库中的一个模块，它提供了许多用于评估预测模型性能的指标和工具。这些指标和工具可以帮助你了解模型在训练集和测试集上的表现，以及模型是否能够很好地泛化到未见过的数据。以下是一些`sklearn.metrics`中常用的函数和指标：1.**分类指标**：-`accuracy_score`:计算分类准确率。-`classification_rep
AI学习记录 - 对抗性神经网络 victor-AI最好的学习方式是画图人工智能学习神经网络
有用点赞哦学习机器学习到一定程度之后，一般会先看他的损失函数是什么，看他的训练集是什么，训练集是什么，代表我使用模型的时候，输入是什么类型的数据。对抗神经网络其实可以这样子理解，网上一直说生成器和判别器的概念，没有触及到本质。我有一种看法：假如当前场景是输入模糊图片，然后输出高质量图片。当判别器和生成器本来就是一个模型，在不把判别器生成器拆开的时候，我输入一张图片，这个模型输出的是0和1，那这个整
机器学习——支持向量机酱香编程，风雨兼程机器学习支持向量机机器学习算法
一、间隔与支持向量给定训练样本集D={(x1,y1),(x2,y2),⋯ ,(xm,ym)},yi∈{−1,+1}D=\{(\bmx_1,y_1),(\bmx_2,y_2),\cdots,(\bmx_m,y_m)\},y_i\in\{-1,+1\}D={(x1,y1),(x2,y2),⋯,(xm,ym)},yi∈{−1,+1}，分类学习最基本的想法就是基于训练集DDD在样本空间中找到一个划分超
第七届MathorCup高校数学建模挑战赛-A题：基于改进的神经网络和混沌时间序列预测控制高炉炼铁过程格图素书大数据竞赛赛题解析数学建模神经网络人工智能
目录摘要一．问题重述二．模型假设三．符号说明四．问题分析五．数据预处理5.1异常值剔除5.2归一化处理5.3预处理后的数据六．问题一模型的建立与求解6.1BP神经网络预测模型6.1.1输入层和输出层6.1.2训练集和验证集6.1.3三层BP神经网络结构6.1.4BP神经网络的参数6.1.6相关性分析6.2小波神经网络预测模型6.2.1小波神经网络的结构6.2.2小波神经网络的基函数6.2.3小波神
PyTorch深度学习模型训练流程的python实现：回归 moyao_miao python 人工智能深度学习 pytorch 回归
回归的流程与分类基本一致，只需要把评估指标改动一下就行。回归输出的是损失曲线、R^2曲线、训练集预测值与真实值折线图、测试集预测值散点图与真实值折线图。输出效果如下：注意：预测值与真实值图像处理为按真实值排序，图中呈现的升序与数据集趋势无关。代码如下：fromfunctoolsimportpartialimportnumpyasnpimportpandasaspdfromsklearn.prepr
基于YOLOv8的无人机高空红外（HIT-UAV）检测算法，新的混合型扩张型残差注意力(HDRAB)助力涨点（二） AI小怪兽深度学习实战应用案列108篇 YOLO 无人机算法 python 开发语言目标检测人工智能
本文内容：针对基于YOLOv8的无人机高空红外（HIT-UAV）检测算法进行性能提升，加入各个创新点做验证性试验。一种新的混合型扩张型残差注意力(HDRAB)，去除图像采集或传输过程中产生的真实噪声(即空间变异噪声)1）混合型扩张型残差注意力(HDRAB)：mAP从原始的0.773提升至0.7791.无人机高空红外数据集介绍无人机高空红外检测数据集大小，训练集2008，验证集287，测试集571张
cnn卷积神经网络反向传播,卷积神经网络维度变化阳阳2013哈哈 PHP cnn 机器学习深度学习神经网络
卷积神经网络是如何反向调整参数的？卷积神经网络反向传播和bp有什么区别如何理解神经网络里面的反向传播算法反向传播算法（Backpropagation）是目前用来训练人工神经网络（ArtificialNeuralNetwork，ANN）的最常用且最有效的算法。其主要思想是：（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；（2）由于ANN的输出结
机器学习：knn算法实现图像识别夜清寒风机器学习算法人工智能
1、概述使用K-近邻（K-NearestNeighbors,KNN）算法对手写数字进行识别的过程。通过读取一张包含多个手写数字的图片，将其分割成单独的数字图像，并将其作为训练和测试数据集。2、数据处理思路1、图像分割该数据有50行100列，每个数字占据20*20个像素点，可以进行切分2、划分出训练集和测试集3、每个数据的像素点为20*20，将其全部变成一列1*400格式，转换成数值特征4、最后使用
基于R语言遥感随机森林建模与空间预测 weixin_贾统计语言类模型分布式
随机森林作为一种集成学习方法，在处理复杂数据分析任务中特别是遥感数据分析中表现出色。通过构建大量的决策树并引入随机性，随机森林在降低模型方差和过拟合风险方面具有显著优势。在训练过程中，使用Bootstrap抽样生成不同的训练集，并在节点分裂时随机选择特征子集，这使得模型具备了处理高维和非线性数据的能力。随机森林对噪声和异常值具有鲁棒性，其预测结果通过对多棵树的集成投票或平均获得，减少了单个异常对结
零基础机器学习(5)之线性回归模型的性能评估一只特立独行猪机器学习机器学习线性回归人工智能
文章目录线性回归模型的性能评估1.举例1-单一特征2.举例2-多特征线性回归模型的性能评估评估线性回归模型时，首先要建立评估的测试数据集（测试集不能与训练集相同），然后选择合适的评估方法，实现对线性回归模型的评估。回归任务中最常用的评估方法有均方误差、均方根误差和预测准确率（确定系数）。1.举例1-单一特征分别对两个模型进行评估，输入的测试集如表所示。面积/（m2）售价/（万元）面积/（m2）售价
深度学习的一个完整过程通常包括以下几个步骤 longerVR DL 深度学习人工智能
深度学习的一个完整过程通常包括以下几个步骤：问题定义和数据收集：定义清晰的问题，明确任务的类型（分类、回归、聚类等）以及预期的输出。收集和整理用于训练和评估模型的数据集。确保数据集的质量，进行预处理和清理。数据预处理：处理缺失值、异常值和重复数据。进行特征工程，选择、转换或创建合适的特征。将数据集划分为训练集、验证集和测试集。选择模型架构：根据问题的性质选择适当的深度学习模型架构，如卷积神经网络（
【机器学习笔记】 9 集成学习 RIKI_1 机器学习机器学习笔记集成学习
集成学习方法概述Bagging从训练集中进行子抽样组成每个基模型所需要的子训练集，对所有基模型预测的结果进行综合产生最终的预测结果：假设一个班级每个人的成绩都不太好，每个人单独做的考卷分数都不高，但每个人都把自己会做的部分做了，把所有考卷综合起来得到成绩就会比一个人做的高Boosting训练过程为阶梯状，基模型按次序一一进行训练（实现上可以做到并行），基模型的训练集按照某种策略每次都进行一定的转化
tenorflow 小鱼儿小于儿 tensorflow
tensorflow笔记3MNIST数据集共7万张图片，都是28*28像素点的手写数字图片。6万张用于训练，1万张用于测试。importtensorflowastfmnist=tf.keras.datasets.mnist(x_train,y_train),(x_test,y_test)=mnist.load_data()#直接送数据集中读取训练集和测试机x_train,x_test=x_trai
【面经——《广州敏视数码科技有限公司》——图像处理算法工程师-深度学习方向】有情怀的机械男面试offer 面经
目录笔试HR面专业面——60多分钟主管面反问：笔试8道题——简答题+1道编程苹果、香蕉、梨、菠萝，彩色图像如何进行分类？一辆带车牌的汽车，图像亮度整体呈现偏亮状态，如何去提高图像的清晰度？并设计一个准确定位车牌位置的方案。训练集和测试集各5000张，进行目标检测，写出选择的模型以及设计方案？样本量不足怎么去提高检测的准确性？数据增强梯度下降法的优化算法有哪些，各有什么优缺点？损失函数有哪些？优缺点
【机器学习笔记】13 降维 RIKI_1 机器学习机器学习笔记人工智能
降维概述维数灾难维数灾难(CurseofDimensionality)：通常是指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。在很多机器学习问题中，训练集中的每条数据经常伴随着上千、甚至上万个特征。要处理这所有的特征的话，不仅会让训练非常缓慢，还会极大增加搜寻良好解决方案的困难。这个问题就是我们常说的维数灾难。维数灾难涉及数字分析、抽样、组合、机器学习、数据挖掘和数据库
【机器学习笔记】8 决策树 RIKI_1 机器学习机器学习笔记决策树
决策树原理决策树是从训练数据中学习得出一个树状结构的模型。决策树属于判别模型。决策树是一种树状结构，通过做出一系列决策（选择）来对数据进行划分，这类似于针对一系列问题进行选择。决策树的决策过程就是从根节点开始，测试待分类项中对应的特征属性，并按照其值选择输出分支，直到叶子节点，将叶子节点的存放的类别作为决策结果。以下小美相亲的例子就是决策树决策树算法是一种归纳分类算法，它通过对训练集的学习，挖掘出
Algorithm 香水浓 java Algorithm
冒泡排序 public static void sort(Integer[] param) { for (int i = param.length - 1; i > 0; i--) { for (int j = 0; j < i; j++) { int current = param[j]; int next = param[j + 1];
mongoDB 复杂查询表达式开窍的石头 mongodb
1:count Pg: db.user.find().count(); 统计多少条数据 2:不等于$ne Pg: db.user.find({_id:{$ne:3}},{name:1,sex:1,_id:0}); 查询id不等于3的数据。 3：大于$gt $gte(大于等于) &n
Jboss Java heap space异常解决方法, jboss OutOfMemoryError : PermGen space 0624chenhong jvm jboss
转自 http://blog.csdn.net/zou274/article/details/5552630 解决办法： window->preferences->java->installed jres->edit jre 把default vm arguments 的参数设为-Xms64m -Xmx512m ----------------
文件上传下载解析相对路径不懂事的小屁孩文件上传
有点坑吧，弄这么一个简单的东西弄了一天多，身边还有大神指导着，网上各种百度着。下面总结一下遇到的问题：文件上传，在页面上传的时候，不要想着去操作绝对路径，浏览器会对客户端的信息进行保护，避免用户信息收到攻击。在上传图片，或者文件时，使用form表单来操作。前台通过form表单传输一个流到后台，而不是ajax传递参数到后台，代码如下: <form action=&
怎么实现qq空间批量点赞换个号韩国红果果 qq
纯粹为了好玩！！逻辑很简单 1 打开浏览器console；输入以下代码。先上添加赞的代码 var tools={}; //添加所有赞 function init(){ document.body.scrollTop=10000; setTimeout(function(){document.body.scrollTop=0;},2000);//加
判断是否为中文灵静志远中文
方法一： public class Zhidao { public static void main(String args[]) { String s = "sdf灭礌 kjl d{';\fdsjlk是"; int n=0; for(int i=0; i<s.length(); i++) { n = (int)s.charAt(i); if((
一个电话面试后总结 a-john 面试
今天，接了一个电话面试，对于还是初学者的我来说，紧张了半天。面试的问题分了层次，对于一类问题，由简到难。自己觉得回答不好的地方作了一下总结：在谈到集合类的时候，举几个常用的集合类，想都没想，直接说了list,map。然后对list和map分别举几个类型： list方面：ArrayList,LinkedList。在谈到他们的区别时，愣住了
MSSQL中Escape转义的使用 aijuans MSSQL
IF OBJECT_ID('tempdb..#ABC') is not null drop table tempdb..#ABC create table #ABC ( PATHNAME NVARCHAR(50) ) insert into #ABC SELECT N'/ABCDEFGHI' UNION ALL SELECT N'/ABCDGAFGASASSDFA' UNION ALL
一个简单的存储过程 asialee mysql 存储过程构造数据批量插入
今天要批量的生成一批测试数据，其中中间有部分数据是变化的，本来想写个程序来生成的，后来想到存储过程就可以搞定，所以随手写了一个，记录在此： DELIMITER $$ DROP PROCEDURE IF EXISTS inse
annot convert from HomeFragment_1 to Fragment 百合不是茶 android 导包错误
创建了几个类继承Fragment, 需要将创建的类存储在ArrayList<Fragment>中; 出现不能将new 出来的对象放到队列中,原因很简单; 创建类时引入包是:import android.app.Fragment; 创建队列和对象时使用的包是:import android.support.v4.ap
Weblogic10两种修改端口的方法 bijian1013 weblogic 端口号配置管理 config.xml
一.进入控制台进行修改 1.进入控制台: http://127.0.0.1:7001/console 2.展开左边树菜单域结构->环境->服务器-->点击AdminServer(管理) &
mysql 操作指令征客丶 mysql
一、连接mysql 进入 mysql 的安装目录； $ bin/mysql -p [host IP 如果是登录本地的mysql 可以不写 -p 直接 -u] -u [userName] -p 输入密码，回车，接连；二、权限操作［如果你很了解mysql数据库后，你可以直接去修改系统表，然后用 mysql> flush privileges; 指令让权限生效］ 1、赋权 mys
【Hive一】Hive入门 bit1129 hive
Hive安装与配置 Hive的运行需要依赖于Hadoop，因此需要首先安装Hadoop2.5.2，并且Hive的启动前需要首先启动Hadoop。 Hive安装和配置的步骤 1. 从如下地址下载Hive0.14.0 http://mirror.bit.edu.cn/apache/hive/ 2.解压hive，在系统变
ajax 三种提交请求的方法 BlueSkator Ajax jqery
1、ajax 提交请求 $.ajax({ type:"post", url : "${ctx}/front/Hotel/getAllHotelByAjax.do", dataType : "json", success : function(result) { try { for(v
mongodb开发环境下的搭建入门 braveCS 运维
linux下安装mongodb 1）官网下载mongodb-linux-x86_64-rhel62-3.0.4.gz 2）linux 解压 gzip -d mongodb-linux-x86_64-rhel62-3.0.4.gz; mv mongodb-linux-x86_64-rhel62-3.0.4 mongodb-linux-x86_64-rhel62-
编程之美-最短摘要的生成 bylijinnan java 数据结构算法编程之美
import java.util.HashMap; import java.util.Map; import java.util.Map.Entry; public class ShortestAbstract { /** * 编程之美最短摘要的生成 * 扫描过程始终保持一个[pBegin,pEnd]的range,初始化确保[pBegin,pEnd]的ran
json数据解析及typeof chengxuyuancsdn js typeof json解析
// json格式 var people='{"authors": [{"firstName": "AAA","lastName": "BBB"},' +' {"firstName": "CCC&
流程系统设计的层次和目标 comsci 设计模式数据结构 sql 框架脚本
流程系统设计的层次和目标
RMAN List和report 命令 daizj oracle list report rman
LIST 命令使用RMAN LIST 命令显示有关资料档案库中记录的备份集、代理副本和映像副本的信息。使用此命令可列出： • RMAN 资料档案库中状态不是AVAILABLE 的备份和副本 • 可用的且可以用于还原操作的数据文件备份和副本 • 备份集和副本，其中包含指定数据文件列表或指定表空间的备份 • 包含指定名称或范围的所有归档日志备份的备份集和副本 • 由标记、完成时间、可
二叉树:红黑树 dieslrae 二叉树
红黑树是一种自平衡的二叉树,它的查找,插入,删除操作时间复杂度皆为O(logN),不会出现普通二叉搜索树在最差情况时时间复杂度会变为O(N)的问题. 红黑树必须遵循红黑规则,规则如下 1、每个节点不是红就是黑。 2、根总是黑的 &
C语言homework3，7个小题目的代码 dcj3sjt126com c
1、打印100以内的所有奇数。 # include <stdio.h> int main(void) { int i; for (i=1; i<=100; i++) { if (i%2 != 0) printf("%d ", i); } return 0; } 2、从键盘上输入10个整数，
自定义按钮, 图片在上, 文字在下, 居中显示 dcj3sjt126com 自定义
#import <UIKit/UIKit.h> @interface MyButton : UIButton -(void)setFrame:(CGRect)frame ImageName:(NSString*)imageName Target:(id)target Action:(SEL)action Title:(NSString*)title Font:(CGFloa
MySQL查询语句练习题，测试足够用了 flyvszhb sql mysql
http://blog.sina.com.cn/s/blog_767d65530101861c.html 1.创建student和score表 CREATE TABLE student ( id INT(10) NOT NULL UNIQUE PRIMARY KEY , name VARCHAR
转：MyBatis Generator 详解 happyqing mybatis
MyBatis Generator 详解 http://blog.csdn.net/isea533/article/details/42102297 MyBatis Generator详解 http://git.oschina.net/free/Mybatis_Utils/blob/master/MybatisGeneator/MybatisGeneator.
让程序员少走弯路的14个忠告 jingjing0907 工作计划学习
无论是谁，在刚进入某个领域之时，有再大的雄心壮志也敌不过眼前的迷茫：不知道应该怎么做，不知道应该做什么。下面是一名软件开发人员所学到的经验，希望能对大家有所帮助 1.不要害怕在工作中学习。只要有电脑，就可以通过电子阅读器阅读报纸和大多数书籍。如果你只是做好自己的本职工作以及分配的任务，那是学不到很多东西的。如果你盲目地要求更多的工作，也是不可能提升自己的。放
nginx和NetScaler区别流浪鱼 nginx
NetScaler是一个完整的包含操作系统和应用交付功能的产品，Nginx并不包含操作系统，在处理连接方面，需要依赖于操作系统，所以在并发连接数方面和防DoS攻击方面，Nginx不具备优势。 2.易用性方面差别也比较大。Nginx对管理员的水平要求比较高，参数比较多，不确定性给运营带来隐患。在NetScaler常见的配置如健康检查，HA等，在Nginx上的配置的实现相对复杂。 3.策略灵活度方
第11章动画效果（下） onestopweb 动画
index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
FAQ - SAP BW BO roadmap blueoxygen BO BW
http://www.sdn.sap.com/irj/boc/business-objects-for-sap-faq Besides, I care that how to integrate tightly. By the way, for BW consultants, please just focus on Query Designer which i
关于java堆内存溢出的几种情况 tomcat_oracle java jvm jdk thread
【情况一】：　　 java.lang.OutOfMemoryError: Java heap space：这种是java堆内存不够，一个原因是真不够，另一个原因是程序中有死循环；　　如果是java堆内存不够的话，可以通过调整JVM下面的配置来解决：　　<jvm-arg>-Xms3062m</jvm-arg> 　　<jvm-arg>-Xmx
Manifest.permission_group权限组阿尔萨斯 Permission
结构继承关系 public static final class Manifest.permission_group extends Object java.lang.Object android. Manifest.permission_group 常量 ACCOUNTS 直接通过统计管理器访问管理的统计 COST_MONEY可以用来让用户花钱但不需要通过与他们直接牵涉的权限 D

数位DP专题

你可能感兴趣的:(训练集)