ACM-博弈专题
基本解题思路
( 1 ) (1) (1) 通过 S G SG SG函数的转移解决问题。
( 2 ) (2) (2) 寻找博弈模型
( 3 ) (3) (3) 对称建立优势
S G SG SG函数
设 N N N为先手必胜态, P P P为后手必胜态。
S G SG SG 函数主要利用了其定义以判断当前的胜负状态。往往最终局面的 S G SG SG 函数值被设为 0 0 0,且当 S G SG SG 函数值为 0 0 0 时当前局面被认为是 P P P 状态,反之是一个 N N N 状态。这个结论是巧妙地和定义结合在一起的,因为若 ∀ S G ( v ) ≠ 0 ∀SG(v)≠0 ∀SG(v)̸=0,则 S G ( u ) = 0 SG(u)=0 SG(u)=0,对应了 P P P 状态的后继状态都是 N N N 状态;若 ∃ S G ( v ) = 0 ∃SG(v)=0 ∃SG(v)=0,则 S G ( u ) ≠ 0 SG(u)≠0 SG(u)̸=0,对应了一个 N N N 状态总有一个后继状态是 P P P 状态。
具体定义:
我们规定一个对于集合的操作 m e x mex mex,表示最小的不属于该集合的非负整数。 如: m e x { 0 , 1 , 2 } = 3 , m e x { 1 , 2 , 3 } = 0 , m e x { 0 , 1 , 3 } = 2 mex\{0,1,2\}=3,mex\{1,2,3\}=0,mex\{0,1,3\}=2 mex{0,1,2}=3,mex{1,2,3}=0,mex{0,1,3}=2;
定义 S G SG SG函数: S G ( x ) = m e x { S G ( y ) ∣ y SG(x)=mex\{ SG(y) | y SG(x)=mex{SG(y)∣y是 x x x的后继,也就是经过操作可以取得的剩下值 } \} }。
比如一堆石子,我们可以取任意个,那么 x x x个石子的石子的 S G SG SG值是多少呢?
可以知道, 0 0 0个石子 S G SG SG为 0 0 0,一的时候我们可以取一个,剩下 0 0 0,的 S G SG SG是 0 0 0,那么 m e x ( 0 ) mex(0) mex(0)就是 1 1 1,所以 1 1 1的 S G SG SG为 1 1 1。
递推下去当为x的时候我们可以取 1 − x 1-x 1−x个,那么剩下的值石子个数就是 x − 1 x-1 x−1到 0 0 0个,他的 m e x ( … ) mex(\dots) mex(…)就是 x x x,所以这个例子的 x x x值的 S G SG SG值就是 x x x;
S G SG SG定理:
博弈的 S G SG SG 值是各个子博弈的 S G SG SG 值的 x o r xor xor。
N i m Nim Nim博弈
问题原型:
给出n堆石子的数量,两人轮流从一堆中取出至少一个石子,先取完者获胜。
结论:
设 N N N为先手必胜态, P P P为后手必胜态。
当 a 1 ⊕ a 2 ⊕ ⋯ ⊕ a i ⊕ ⋯ ⊕ a n = 0 a_1\oplus\ a_2\oplus\dots\oplus a_i\oplus\dots\oplus a_n =0 a1⊕ a2⊕⋯⊕ai⊕⋯⊕an=0 时,为 P P P态,否则为 N N N态。
证明:
证明等价于证明以下三个结论:
( 1 ) (1) (1) 证明空状态为 P P P。
( 2 ) (2) (2) 每一个 N N N都能通过取走一些石头而转化为 P P P。
( 3 ) (3) (3) P P P不能通过取走一些石头而转化为 P P P。
( 1 ) (1) (1) 显然,当 a 1 = a 2 = ⋯ = a n = 0 a_1=a_2=\dots=a_n=0 a1=a2=⋯=an=0时,后手必胜。
( 2 ) (2) (2) 当 a 1 ⊕ a 2 ⊕ ⋯ ⊕ a i ⊕ ⋯ ⊕ a n = k a_1\oplus\ a_2\oplus\dots\oplus a_i\oplus\dots\oplus a_n =k a1⊕ a2⊕⋯⊕ai⊕⋯⊕an=k时,必定存在 a i a_i ai,使得 a i ⊕ k < a i a_i\oplus k<a_i ai⊕k<ai,此时只需要令 a i ′ = a i ⊕ k a_i'=a_i\oplus k ai′=ai⊕k,使得 a 1 ⊕ a 2 ⊕ ⋯ ⊕ a i ′ ⊕ ⋯ ⊕ a n = 0 a_1\oplus\ a_2\oplus\dots\oplus a_i'\oplus\dots\oplus a_n =0 a1⊕ a2⊕⋯⊕ai′⊕⋯⊕an=0,此时由 N N N转化为 P P P。
( 3 ) (3) (3) 对于 a 1 ⊕ a 2 ⊕ ⋯ ⊕ a i ⊕ ⋯ ⊕ a n = 0 a_1\oplus\ a_2\oplus\dots\oplus a_i\oplus\dots\oplus a_n =0 a1⊕ a2⊕⋯⊕ai⊕⋯⊕an=0且 a 1 ⊕ a 2 ⊕ ⋯ ⊕ a i ′ ⊕ ⋯ ⊕ a n = 0 a_1\oplus\ a_2\oplus\dots\oplus a_i'\oplus\dots\oplus a_n =0 a1⊕ a2⊕⋯⊕ai′⊕⋯⊕an=0,由群相关结论很容易得出 a i = a i ′ a_i=a_i' ai=ai′,不符合规则。
以上得证。
例题:
下面是一个二人小游戏:桌子上有M堆扑克牌;每堆牌的数量分别为 n i ( i = 1 … m ) n_i(i=1\dots m) ni(i=1…m);两人轮流进行;每走一步可以任意选择一堆并取走其中的任意张牌;桌子上的扑克全部取光,则游戏结束;最后一次取牌的人为胜者。
现在我们不想研究到底先手为胜还是为负,我只想问大家:
——“先手的人如果想赢,第一步有几种选择呢?”
题解:
若 n 1 ⊕ n 2 ⊕ ⋯ ⊕ n i ⊕ ⋯ ⊕ n m = 0 n_1\oplus\ n_2\oplus\dots\oplus n_i\oplus\dots\oplus n_m =0 n1⊕ n2⊕⋯⊕ni⊕⋯⊕nm=0,则先手必输,输出0。
若 n 1 ⊕ n 2 ⊕ ⋯ ⊕ n i ⊕ ⋯ ⊕ n m = k n_1\oplus\ n_2\oplus\dots\oplus n_i\oplus\dots\oplus n_m =k n1⊕ n2⊕⋯⊕ni⊕⋯⊕nm=k,则输出满足 a i ⊕ k < a i a_i\oplus k<a_i ai⊕k<ai的 i i i的个数。
反 N i m Nim Nim博弈
问题原型:
给出n堆石子的数量,两人轮流从一堆中取出至少一个石子,最后一个取的人输。
结论:
在反尼姆博奕中判断必胜局面的条件有两点,满足任意一点先手都能取胜,即必胜局面。
( 1 ) : (1): (1): 各堆石子数目异或结果不等于0,且存在有石子数目大于1的石子堆。
( 2 ) (2) (2): 所有石子堆均为1,且总堆数为偶数。
阶梯博弈 (变种 N i m Nim Nim博弈)
问题原型:
有n个阶梯呈升序排列,每个阶梯上有若干个石子,可行的操作是将一个阶梯上的石子移任意个(>0)到前一个台阶。当没有可行操作时(所有石子都被移动到了地面,即第0号台阶)输。
结论:
等价于奇数台阶上的 N i m Nim Nim博弈。
证明:
( 1 ) (1) (1) 如果对手移动偶数位上的石子,只需要将这些石子再向下移动一位。对结果无影响。
( 2 ) (2) (2) 将奇数位上的石子移动至偶数位,由结论 ( 1 ) (1) (1)可知,相当于将这些石子移除。
( 3 ) (3) (3) 由以上结论可得,阶梯博弈相当于奇数位上的 N i m Nim Nim博弈。
N i m k Nimk Nimk 博弈(变种 N i m Nim Nim博弈)
问题原型:
变种 ( 1 ) (1) (1):每次最多从一堆中取 k k k 个
变种 ( 2 ) (2) (2):每轮能取最多 k k k 堆,从这k堆中每堆中取数量任意的石子。(不同堆取石子的数量可以不同)
结论:
变种 ( 1 ) (1) (1):只需将每堆石子数对 ( k + 1 ) (k+1) (k+1)取模
变种 ( 2 ) (2) (2):设 a i a_i ai表示 a a a的二进制中的第 i i i位, b i b_i bi表示 b b b的二进制中的第 i i i位。只需定义 a ⊕ b = ( a + b ) m o d ( k + 1 ) a\oplus b=(a+b)\bmod(k+1) a⊕b=(a+b)mod(k+1)。( 即: k = 1 k=1 k=1时, a ⊕ b = ( a + b ) m o d 2 a\oplus b=(a+b)\bmod 2 a⊕b=(a+b)mod2 )
证明:
与 N i m Nim Nim博弈类似。
线性翻硬币博弈
问题原型:
N N N 枚硬币排成一排,有的正面朝上,有的反面朝上。我们从左开始对硬币按 1 1 1 到 N N N 编号。
第一,游戏者根据某些约束翻硬币,但他所翻动的硬币中,最右边那个硬币的必须是从正面翻到反面。例如,只能翻 3 3 3个硬币的情况,那么第三个硬币必须是从正面翻到反面。如果局面是正正反,那就不能翻硬币了,因为第三个是反的。
第二,谁不能翻谁输。
结论:
局面的 S G SG SG 值为局面中每个正面朝上的棋子单一存在时的 S G SG SG 值的异或和。即一个有 k k k个硬币朝上,朝上硬币位置分布在的翻硬币游戏中, S G SG SG值是等于 k k k个独立的开始时只有一个硬币朝上的翻硬币游戏的 S G SG SG值异或和。比如 T H H T T H THHTTH THHTTH这个游戏中, 2 2 2号、 3 3 3号、 6 6 6号位是朝上的,它等价于 T H 、 T T H 、 T T T T T H TH、TTH、TTTTTH TH、TTH、TTTTTH三个游戏和,即 s g [ T H H T T H ] = s g [ T H ] ⊕ s g [ T T H ] ⊕ s g [ T T T T T H ] sg[THHTTH]=sg[TH]\oplus sg[TTH]\oplus sg[TTTTTH] sg[THHTTH]=sg[TH]⊕sg[TTH]⊕sg[TTTTTH]。我们的重点就可以放在单个硬币朝上时的 S G SG SG值的求法。
例题:
在各种具体约束条件下的翻硬币博弈求解:博弈-翻硬币游戏 。
二维/三维翻硬币博弈( N i m Nim Nim和、 N i m Nim Nim积运算)
问题原型:
( 1 ) (1) (1)
在 n + 1 n+1 n+1行和 m + 1 m+1 m+1列的棋盘上,坐标从 ( 0 , 0 ) (0,0) (0,0)到 ( n , m ) (n,m) (n,m),每个格子有一枚硬币。两个玩家轮流操作,每次同时翻转同一列或者同一行的两枚硬币。且:横纵坐标最大的那枚硬币必须是由正面翻到反面。
两边轮流操作直至一方无法操作,无法操作的判负。
( 2 ) (2) (2)
在 n + 1 n+1 n+1行和 m + 1 m+1 m+1列的棋盘上,坐标从 ( 0 , 0 ) (0,0) (0,0)到 ( n , m ) (n,m) (n,m),每个格子有一枚硬币。两个玩家轮流操作,每次同时翻转在一个矩形四个顶点上的硬币,并且要求,每次操作时,矩形横纵坐标最大的格子中的硬币必须是由正面翻到反面。两边轮流操作直至一方无法操作,无法操作的判负。
( 3 ) (3) (3)
三维棋盘,其余与 ( 2 ) (2) (2)类似。
结论:
( 1 ) (1) (1) S G ( x , y ) = x ⊕ y SG(x,y)=x\oplus y SG(x,y)=x⊕y。
( 2 ) (2) (2) S G ( x , y ) = x ⊗ y SG(x,y)=x\otimes y SG(x,y)=x⊗y
( 3 ) (3) (3) S G ( x , y , z ) = x ⊗ y ⊗ z SG(x,y,z)=x\otimes y\otimes z SG(x,y,z)=x⊗y⊗z
⊗ \otimes ⊗实现代码:
int m[2][2]={0,0,0,1};
int Nim_Multi_Power(int x,int y) //辅助函数
{
if(x<2)
return m[x][y];
int a=0;
for(;;a++)
if(x>=(1<<(1<<a))&&x<(1<<(1<<(a+1))))
break;
int m=1<<(1<<a);
int p=x/m,s=y/m,t=y%m;
int d1=Nim_Multi_Power(p,s);
int d2=Nim_Multi_Power(p,t);
return (m*(d1^d2))^Nim_Multi_Power(m/2,d1);
}
int Nim_Multi(int x,int y) //求解函数
{
if(x<y)
return Nim_Multi(y,x);
if(x<2)
return m[x][y];
int a=0;
for(;;a++)
if(x>=(1<<(1<<a))&&x<(1<<(1<<(a+1))))
break;
int m=1<<(1<<a);
int p=x/m,q=x%m,s=y/m,t=y%m;
int c1=Nim_Multi(p,s);
int c2=Nim_Multi(p,t)^Nim_Multi(q,s);
int c3=Nim_Multi(q,t);
return (m*(c1^c2))^c3^Nim_Multi_Power(m/2,c1);
}
树上删边博弈(类 N i m Nim Nim博弈、克朗原理)
问题原型:
在某一棵树上删除一条边,同时删去所有在删除后不再与根相连的部分
双方轮流操作,先删除完者获胜。
结论
为了更好理解该博弈模型,我们引入“竹子”的概念:
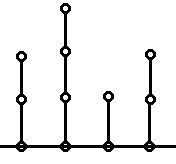
根据上面的游戏规则,拿掉竹子上的某一节,那么此节上面的部分都会被删除。这就是Nim博弈的变形。其对应的 S G [ x ] = x SG[x]=x SG[x]=x。
我们把竹子的形态变的稍微复杂一点,在竹子上加一些分支,就可以得到一棵朴素的树。
首先介绍克朗原理:
克朗原理:
对于树上的某一个点,ta的分支可以转化成以这个点为根的一根竹子,这个竹子的长度就是ta各个分支的边的数量的异或和。
举例:
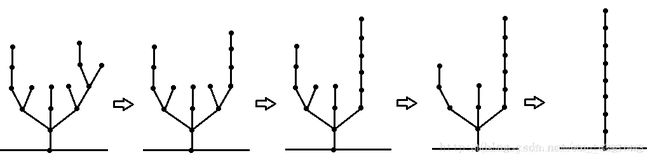
在这棵树中,其 S G SG SG函数值为 8 8 8。
我们可以得到类似的结论: S G [ x ] = 0 SG[x]=0 SG[x]=0时,后手必胜,否则先手必胜。
图上删边博弈(费森原理)
问题原型:
类似树上删边,在某一幅无向图上删除一条边,同时删去所有在删除后不再与根相连的部分 。双方轮流操作,先删除完者获胜。
结论:
例图:

我们当然希望把上图也转化成一个树形结构,之后利用克朗原理转化成竹子,变成Nim博弈解决 。
首先介绍费森原理:
费森原理
环上的点可以融合,且不改变图的 S G SG SG值。
可以发现,上图中门是独立于整个大框外的,所以我们从门开始。
首先,我们可以把地板上的两个点视为一个,因为地板本身就可以看成是一个大点
这样这扇门就变成一个三角形(一个有三个点的环)
费森原理指出,我们可以把环上一个点等价成一个自环,而这个环又可以变成一条边

一般来说 :
我们可以把一个带有奇数边的环等价成只有一个端点的一条边 ,
而偶数边的环等价于一个点。
有了这个结论,就简单多了
因此,上图中房子的烟囱和窗户都可以等价成一个点
那我们继续我们的化简:
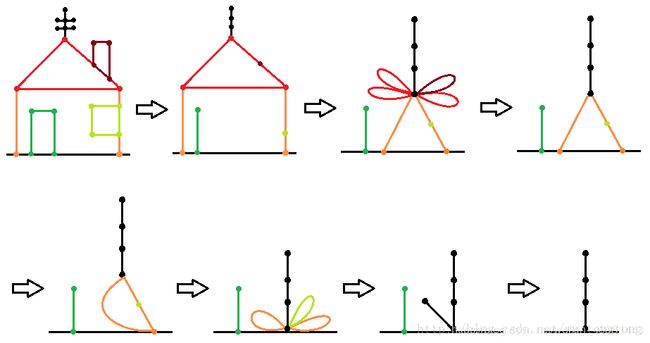
从上面所有的讨论中,我们可以得到启发:
对于博弈的大部分问题,只要 S G SG SG值相同,就可以互相转化。
E v e r y Every Every S G SG SG博弈
问题原型:
由 n n n个游戏同时进行,除非游戏结束,否则必须操作。取最后一次的获胜情况为结果。
结论:
这个整体博弈的思路是:如果某个子游戏自己必胜,使游戏总步数尽量多。如果必败,使游戏总步数尽量少。
对于该博弈,先手必胜当且仅当所有子博弈中的最大的 s t e p step step为奇数。
实现:
对于一个子游戏的情况 v v v,如果 S G ( v ) = 0 SG(v)=0 SG(v)=0,我们需要知道其最快几步能将状态转化为终止状态。如果 S G ( v ) ≠ 0 SG(v)\ne0 SG(v)̸=0,我们需要知道其最快几步能将状态转化为终止状态。我们用 s t e p ( v ) step(v) step(v)表示这个值。则:
s t e p ( v ) = { 0 v 为终止态 max { s t e p ( u ) } + 1 S G ( v ) ≠ 0 且 S G ( u ) = 0 min { s t e p ( u ) } + 1 S G ( v ) = 0 且 S G ( v ) = 0 step(v)=\left\{\begin{aligned} &0&v\text{为终止态} \\&\max\{step(u)\}+1&SG(v)\ne0\text{且}SG(u)=0 \\&\min\{step(u)\}+1&SG(v)=0\text{且}SG(v)=0 \end{aligned}\right. step(v)=⎩⎪⎨⎪⎧0max{step(u)}+1min{step(u)}+1v为终止态SG(v)̸=0且SG(u)=0SG(v)=0且SG(v)=0、
其中 u u u为 v v v的后继状态。
D A G DAG DAG问题
这一类问题中, S G SG SG 函数的用法显而易见,也有很多很多问题可以转化为此类问题。
在这一类问题中,前驱与后继状态清晰明了,而且往往没有显然的规律,以至于出题人会给你充足的时间让你把各种起手的状态处理一遍。这时就要用到 S G SG SG 函数了,而且很显然是让你把起手时的 S G SG SG 函数值推出来存下来 …… 于是就可以将其他的一些问题也对应到 D A G DAG DAG 上,然后直接通过 S G SG SG 函数之间的转移而解决几乎全部的问题。(即:打表找规律)
威佐夫博弈 (Wythoff Game)
问题原型:
给出两堆石子的数量,两人轮流从一堆取出至少一个或同时从两堆中取出相同数量的石子,先取完者获胜。
结论:
我们用 ( a i , b i ) (a_i,b_i) (ai,bi)表示两堆石子的数量,并称其为“局势”。将后手必赢的局势称为奇异局势。
奇异局势有: ( 0 , 0 ) , ( 1 , 2 ) , ( 3 , 5 ) , ( 4 , 7 ) , ( 6 , 10 ) , ( 8 , 13 ) , ( 9 , 15 ) , ( 11 , 18 ) , … , ( a k , b k ) (0,0),(1,2),(3,5),(4,7),(6,10),(8,13),(9,15),(11,18),\dots ,(a_k,b_k) (0,0),(1,2),(3,5),(4,7),(6,10),(8,13),(9,15),(11,18),…,(ak,bk)。(排列规则为 b i ⩾ a i b_i\geqslant a_i bi⩾ai 且 a i a_i ai增序排列)
我们发现奇异局势有如下特点:
( 1 ) (1) (1) a k a_k ak为前 k − 1 k-1 k−1 个奇异局势中未曾出现过的最小正整数。
( 2 ) (2) (2) 对于第 k k k 个奇异局势 ( a k , b k ) (a_k,b_k) (ak,bk), b k − a k = ( k − 1 ) b_k-a_k=(k-1) bk−ak=(k−1)。
( 3 ) (3) (3) a k = ( b k − a k ) ∗ 0.618 a_k=(b_k-a_k)*0.618 ak=(bk−ak)∗0.618。
证明:
略。
斐波那契博弈
问题原型:
有一堆个数为 n n n的石子,游戏双方轮流取石子,满足:
1 ) 1) 1) 先手不能在第一次把所有的石子取完;
2 ) 2) 2) 之后每次可以取的石子数介于 1 1 1 到对手刚取的石子数的 2 2 2倍 之间(包含 1 1 1 和对手刚取的石子数的 2 2 2 倍)。
约定取走最后一个石子的人为赢家。
结论:
先手获胜当且仅当 n n n不是斐波那契数。
证明:
( 1 ) (1) (1) 先证明当 n n n为斐波那契数时,先手必败。
n = f i b ( 2 ) n=fib(2) n=fib(2) 时,显然先手必败。
假设 n ⩽ f i b ( k ) n\leqslant fib(k) n⩽fib(k) 时,结论成立。则 n = f i b ( k + 1 ) n=fib(k+1) n=fib(k+1) 时, n n n可分解为 f i b ( k ) + f i b ( k − 1 ) fib(k)+fib(k-1) fib(k)+fib(k−1)。由斐波那契数列的性质可得, f i b ( k ) ⩾ 2 ∗ f i b ( k − 1 ) fib(k)\geqslant 2*fib(k-1) fib(k)⩾2∗fib(k−1),所以先手取得石子数一定小于 f i b ( k − 1 ) fib(k-1) fib(k−1),否则后手能一次全部取完。有假设可得,在 n = f i b ( k − 1 ) n=fib(k-1) n=fib(k−1)的情况时,后手能取走最后一颗石子。所以在这种情况下,后手一定能取完 f i b ( k − 1 ) fib(k-1) fib(k−1)这一部分石子。此时,剩余量为 f i b ( k ) fib(k) fib(k)颗石子,且显然先手无法一次全都取完。再由假设可得,此时一定是后手取走最后一颗石子。所以先手必败。
( 2 ) (2) (2) 证明先手必胜的情况。
由齐肯多夫定理( Z e c k e n d o r f Zeckendorf Zeckendorf定理)可知,任意正整数都能表示成若干不相邻的斐波那契数之和。
令 n = f i b ( a 1 ) + f i b ( a 2 ) + ⋯ + f i b ( a p ) n=fib(a_1)+fib(a_2)+\dots +fib(a_p) n=fib(a1)+fib(a2)+⋯+fib(ap)。( a 1 < a 2 < ⋯ < a p a_1<a_2<\dots <a_p a1<a2<⋯<ap)
由斐波那契数列性质可得, f i b ( k ) > 2 ∗ f i b ( k − 2 ) fib(k)>2*fib(k-2) fib(k)>2∗fib(k−2),此时,先手只要取走 f i b ( a 1 ) fib(a_1) fib(a1)颗石子,由于 a 1 , a 2 , … , a p a_1,a_2,\dots,a_p a1,a2,…,ap不连续,所以后手方取的石子数一定小于 f i b ( a 2 ) fib(a_2) fib(a2),由证明 ( 1 ) (1) (1)得,对于 f i b ( a 2 ) fib(a_2) fib(a2) 个石子,后手(该情况下的先手)一定能取到最后一个。以此递推,先手一定能取到最后一个石子。
k k k 倍动态减法博弈(斐波那契博弈变种)
问题原型:
有一堆个数为 n n n的石子,游戏双方轮流取石子,满足:
1 ) 1) 1) 先手不能在第一次把所有的石子取完;
2 ) 2) 2) 之后每次可以取的石子数介于 1 1 1 到对手刚取的石子数的 k k k 倍之间(包含 1 1 1和对手刚取的石子数的 k k k 倍)。
约定取走最后一个石子的人为赢家。
结论:
k = 1 k=1 k=1 时,先手必胜当且仅当 n n n 不是 2 2 2 的次幂。否则,先手只要不停取 l o w b i t ( n ) lowbit(n) lowbit(n)即可取胜。
k = 2 k=2 k=2 时,等同于斐波那契博弈。
k = 3 k=3 k=3 时,构造数列 a ( n ) a(n) a(n),使得其满足如下性质:
对于任意整数 n n n, n n n可分解为 a ( m 1 ) + a ( m 2 ) + ⋯ + a ( m p ) a(m_1)+a(m_2)+\dots +a(m_p) a(m1)+a(m2)+⋯+a(mp)。且对于任意 i i i, a ( m i ) > k ∗ a ( m i + 1 ) a(m_i)>k*a(m_i+1) a(mi)>k∗a(mi+1)。
此时,模仿斐波那契博弈,先手必胜当且仅当 n n n不属于数列 a ( n ) a(n) a(n)。
证明:
同斐波那契博弈。
代码实现:
设数组 a [ ] , b [ ] a[],b[] a[],b[]。
a [ i ] a[i] a[i] 表示这个数列的第 i i i个数, b [ i ] b[i] b[i] 表示用( a [ 1 ] , a [ 2 ] , … , a [ i ] a[1],a[2],\dots ,a[i] a[1],a[2],…,a[i])所能构造出来的最大的数。
显然, a [ i + 1 ] = b [ i ] + 1 a[i+1]=b[i]+1 a[i+1]=b[i]+1, b [ i + 1 ] = a [ i + 1 ] + b [ j ] b[i+1]=a[i+1]+b[j] b[i+1]=a[i+1]+b[j],其中 j j j 为最大的满足 a [ j ] ∗ k < a [ j + 1 ] a[j]*k<a[j+1] a[j]∗k<a[j+1]的数。
a[0]=0;a[1]=1;b[0]=0;b[1]=1;
int i=1;
while(a[i]<n){
a[i+1]=b[i]+1;
int j=0;
while(a[j+1]*k<a[i+1])j++; //这里注意必须从小往大找,不然会TLE
b[i+1]=a[i+1]+b[j];
idex++;
}
对称建立优势
例题:
有 n n n个硬币,将它们围成一个圈。两人轮流翻转至多k个连续的硬币,翻转完者胜。
题解:
( 1 ) (1) (1) 若 k = 1 k=1 k=1,显然奇数先手赢,偶数后手赢。
( 2 ) (2) (2) 若 k ⩾ 2 : k\geqslant 2: k⩾2:
a : a: a: 先手一次取完,先手赢。
b : b: b: 先手不能一次取完,后手只要将剩余部分分为相等两部分,建立对称优势,后手必胜。
多重博弈
问题原型:
玩家进行 k k k次某种游戏,第 i i i次的败者,将会作为第 i + 1 i+1 i+1次的先手进行这个游戏。第 k k k次游戏的赢家才是整个游戏的赢家。
结论:
定义四种状态:先手必胜、先手必败、先手可决定输赢、先手不能控制。
若游戏先手必败或先手不能控制,则后手只要一直胜利就可以取得最终胜利。
若游戏先手必胜,则若 k k k为偶数,则整个游戏后手必胜,若 k k k为奇数,则整个游戏先手必胜。
若游戏先手可决定输赢,则先手只要一直输到最后一局,再赢下去,就能获得游戏胜利。先手必胜。
例题:
有一种游戏:给定 n n n个非空串。两个玩家轮流向一个空字符串后面加字母。每次操作形成的新字符串一定要是这 n n n个串中某一个的前缀,如果无法做到,就输了。
玩家玩 k k k次这样的游戏,第 i i i次的败者,将会作为第 i + 1 i+1 i+1次的先手进行这个游戏。第 k k k次游戏的赢家才是整个游戏的赢家。
题解:
先建立字符串的Trie树。
叶子结点为先手必败态;
若某结点的所有儿子都是先手必败态,则该结点为先手必胜态;
若某结点的所有儿子都是先手必胜态,则该结点为先手必败态;
若某结点的儿子既有先手必胜态,又有先手必败态,或者是存在先手不能控制态,则该状态为先手可决定输赢;
若某结点的所有儿子都是先手可决定输赢,则该结点为先手不能控制。
若某结点的儿子除了可输可赢态外还有其他状态,那么就当可输可赢态不存在。因为,不能将主导权交给对手。
不平等博弈( S u r r e a l Surreal Surreal N u m b e r Number Number)
暂无。待补充。