FFT快速傅立叶变换

学习数学真是一件赛艇的事
FFT是我到目前OI的数学相关学过最难的了
其实理解以后发现并不是很难,只是需要的基础知识比较多

---

前置技能

主要包括复数相关,线性代数相关,分治基础

---

复数相关,复平面向量

可汗学院讲的真不错,强烈推荐看一看,内容比较全面,不过时间有点长
这里对复数做一点简单的总结

定义:

i2=−1 i 2 = − 1

这里的 i i 是虚数单位(imaginary number)
对于任何数 z z 都可以写成形如:

z=a+b∗i z = a + b ∗ i

对于我们之前说的实数,放在这个形式里就是b=0
其中a称为实部, bi b i 称为虚部

---

复数的四则运算

在这里我们只需要掌握加减乘三则运算就好
设 A=a+bi A = a + b i ,  B=c+di B = c + d i

加法:

A+B=(a+c)+(b+d)i A + B = ( a + c ) + ( b + d ) i

减法

A+B=(a−c)+(b−d)i A + B = ( a − c ) + ( b − d ) i

乘法

A∗B=(a+bi)(c+di)=ac+adi+bci+bdi2=ac−bd+adi+bci=(ac−bd)+(ad+bc)i A ∗ B = ( a + b i ) ( c + d i ) = a c + a d i + b c i + b d i 2 = a c − b d + a d i + b c i = ( a c − b d ) + ( a d + b c ) i

共轭复数

若 z=a+bi,z′=a−bi z = a + b i , z ′ = a − b i 则称 z′是z的共轭复数 z ′ 是 z 的 共 轭 复 数

---

复平面

首先定义一个复平面,x轴表示实部,y轴表示虚部
那么任何一个复数都可以在这个平面上以一个向量的形式表示出来

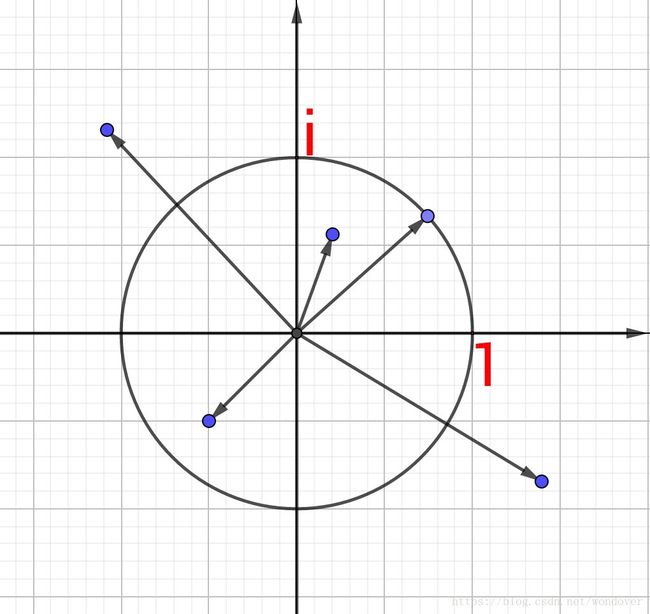
然后考虑四则运算的几何表示
加法和减法依然满足平行四边形法则
乘法根据棣莫弗定理要记住模长相乘,幅角相加

---

单位根

在复平面上以原点为圆心,1为半径作圆得到 单位圆 单 位 圆
设 (ωn)n=1 ( ω n ) n = 1 ,称 ωn ω n 为n次单位根
在复平面上我们可以想象成用n条射线,从实轴开始,把圆均分成n部分
第一条射线与单位圆的交点所形成的向量
假设n=16,如图

(ωn)n ( ω n ) n 就是n个 ωn ω n 相乘(n-1)得到的向量,
因为要满足模长相乘,幅角相加
模长都为1不变,幅角= 2π∗(n−1)n 2 π ∗ ( n − 1 ) n
就相当于
整个平面被均分成了16份,所以旋转15次以后又回到(1,0),所以 ωnn=1 ω n n = 1 .
对于单位根我们要知道它的几个性质

1.  ω2k2n=ωkn ω 2 n 2 k = ω n k

把平面分成2n格,旋转2k格=把平面分成n格,旋转k格.

2.  ωn+kn=ωkn ω n n + k = ω n k

指数函数的性质.

3.  ωn2+kn=−ωkn ω n n 2 + k = − ω n k

因为 omegan2n=−1 o m e g a n n 2 = − 1 .

4.  ωn=cos ω n = cos 2πn+isin 2 π n + i sin 2πn 2 π n

几何性质

---

线性代数相关

对于这一方面要求理解的并不是很多,只要了解矩阵乘法和矩阵的逆就好了
不了解也没有关系,接下来会详细说明

---

多项式乘法

例题:已知两个n次多项式 A=a0+a1x+a2x2+...+anxn A = a 0 + a 1 x + a 2 x 2 + . . . + a n x n 和 B=b0+b1x+b2x2+...+bnxn B = b 0 + b 1 x + b 2 x 2 + . . . + b n x n ,求A*B的各项系数.
首先看到这道题的做法就是 O(n2) O ( n 2 ) 的暴力,将A的每个系数与B的每个系数相乘
想一想有没有可以优化的地方?
然而并没有……
接下来就需要FFT的操作了

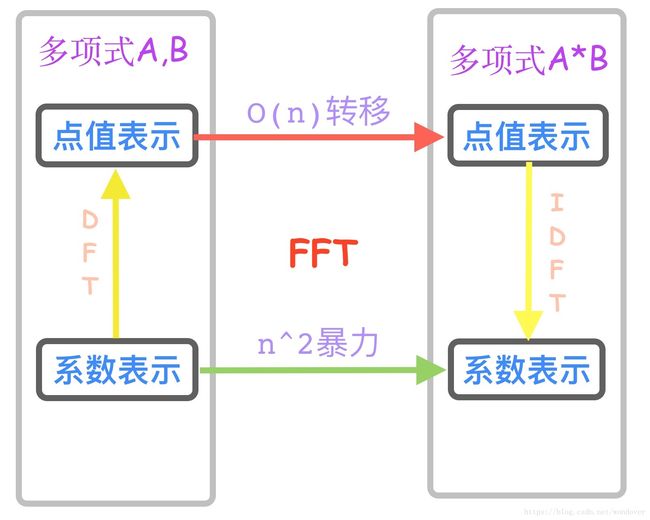
系数表示法与点值表示法

对于一个多项式,我们最常用的把他表示出来的方法是系数表示法
就是形如 A=a0+a1x+a2x2+...+anxn A = a 0 + a 1 x + a 2 x 2 + . . . + a n x n 的式子
其实还有另外一种表示方法点值表示法
(x0,f(x0)),(x1,f(x1)),(x2,f(x2))...(xn,f(xn)). ( x 0 , f ( x 0 ) ) , ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) . . . ( x n , f ( x n ) ) .
就像两点确定一条直线,三点确定一条抛物线一样,n+1个点能确定一个n次多项式
我们发现对于多项式A和B
A=(x0,f(x0)),(x1,f(x1)),(x2,f(x2))...(xn,f(xn)) A = ( x 0 , f ( x 0 ) ) , ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) . . . ( x n , f ( x n ) ) .
B=(x0,g(x0)),(x1,g(x1)),(x2,g(x2))...(xn,g(xn)) B = ( x 0 , g ( x 0 ) ) , ( x 1 , g ( x 1 ) ) , ( x 2 , g ( x 2 ) ) . . . ( x n , g ( x n ) ) .
A∗B=(x0,f(x0) A ∗ B = ( x 0 , f ( x 0 ) ∗ ∗ g(x0)),(x1,f(x1) g ( x 0 ) ) , ( x 1 , f ( x 1 ) ∗ ∗ g(x1))...(xn,f(xn) g ( x 1 ) ) . . . ( x n , f ( x n ) ∗ ∗ g(xn)). g ( x n ) ) .

这个操作是 O(n) O ( n ) 的
这个 O(n) O ( n ) 给我们提供了一个很好的思路,我们可以通过某种方法将系数表示变成点值表示,
再O(n)计算A*B,最后再通过某种方法将点值表示变回系数表示
一张图

考虑第一个奇怪的方法,如果采用暴力赋值计算,复杂度还是 O(n2) O ( n 2 ) 的
快速幂?naive 更慢! O(n2logn) O ( n 2 l o g n )
所以我们不得不采用一种特殊的方法
给你一个多项式

A(x)=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6+...+an−1xn−1 A ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 + a 6 x 6 + . . . + a n − 1 x n − 1

注:之后的所有n都是2的次幂,如果n不满2的次幂可以直接令n向上等于2的次幂,因为n越大,对于答案不会造成影响.
我们设

A0(x)=a0+a2x+a4x2+a6x3+...+an−2xn2 A 0 ( x ) = a 0 + a 2 x + a 4 x 2 + a 6 x 3 + . . . + a n − 2 x n 2

A1(x)=a1+a3x+a5x2+a7x3+...+an−1xn2 A 1 ( x ) = a 1 + a 3 x + a 5 x 2 + a 7 x 3 + . . . + a n − 1 x n 2

可以发现

A(x)=A0(x2)+xA1(x2) A ( x ) = A 0 ( x 2 ) + x A 1 ( x 2 )

然后就是一步骚操作,令 x=ωkn x = ω n k

A(ωkn)=A0(ω2kn)+ωknA1(ω2kn) A ( ω n k ) = A 0 ( ω n 2 k ) + ω n k A 1 ( ω n 2 k )

=A0(ωkn2)+ωknA1(ωkn2) = A 0 ( ω n 2 k ) + ω n k A 1 ( ω n 2 k )

又令 x=ωn2+kn x = ω n n 2 + k

A(ωn2+kn)=A0(ωn+2kn)+ωn2+knA1(ωn+2kn) A ( ω n n 2 + k ) = A 0 ( ω n n + 2 k ) + ω n n 2 + k A 1 ( ω n n + 2 k )

=A0(ω2kn)−ωknA1(ω2kn) = A 0 ( ω n 2 k ) − ω n k A 1 ( ω n 2 k )

=A0(ωkn2)−ωknA1(ωkn2) = A 0 ( ω n 2 k ) − ω n k A 1 ( ω n 2 k )

比较上面两个式子,我们发现
假设我们已经知道了 A0(ωkn2) A 0 ( ω n 2 k ) 和 A1(ωkn2) A 1 ( ω n 2 k ) ,我们就能同时知道 A(ωkn) A ( ω n k ) 和 ωn2+kn ω n n 2 + k .
这样就把问题缩小了一半,对于每个问题都缩小一半,复杂度就从 O(n2) O ( n 2 ) 变成了 O(nlogn) O ( n l o g n ) .
就可以利用一种类似于线段树的操作来计算,如果没有理解就看看这张盗来的图

每一层向上转移是 O(n)的 O ( n ) 的 ,因为树高只有 logn l o g n 层,总复杂度就变得很小
此时我们的第一步由系数到点值已经结束了,不过还要补充一点
观察树的最底层
序列为 0,4,2,6,1,5,3,7 0 , 4 , 2 , 6 , 1 , 5 , 3 , 7
原序列 0,1,2,3,4,5,6,7 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7
转化成二进制来发现规律
新序列 000,100,010,110,101,011,111 000 , 100 , 010 , 110 , 101 , 011 , 111
原序列 000,001,010,011,101,110,111 000 , 001 , 010 , 011 , 101 , 110 , 111
我们发现新序列的每个数是原序列的二进制反转
现在我们已经知道了每个序列的下标,我们就可以利用下标实现
这种实现方法更像是倍增,而不是分治,虽然算法的本质还是分治
如果要看代码在最后面…

---

IDFT

对于把点值表示转化成系数表示,我们已经知道了用分治的方法快速求.
抛开分治以及log算法不谈,我们可以从另一方面理解刚才的操作

线性代数

把所有系数放在一起组成一个系数列向量:

⎡⎣⎢⎢⎢⎢⎢⎢a0a1a2⋮an−1⎤⎦⎥⎥⎥⎥⎥⎥ [ a 0 a 1 a 2 ⋮ a n − 1 ]

最终的n个点值也可以放在一起组成一个点值列向量

⎡⎣⎢⎢⎢⎢⎢⎢y0y1y2⋮yn−1⎤⎦⎥⎥⎥⎥⎥⎥ [ y 0 y 1 y 2 ⋮ y n − 1 ]

系数列向量可以通过左乘一个矩阵得到点值列向量

⎡⎣⎢⎢⎢⎢⎢⎢(x0)0(x1)0(x2)0⋮(xn−1)0(x0)1(x1)1(x2)1⋮(xn−1)1(x0)2(x1)2(x2)2⋮(xn−1)2⋯⋯⋯⋱⋯(x0)n−1(x1)n−1(x2)n−1⋮(xn−1)n−1⎤⎦⎥⎥⎥⎥⎥⎥∗⎡⎣⎢⎢⎢⎢⎢⎢a0a1a2⋮an−1⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢y0y1y2⋮yn−1⎤⎦⎥⎥⎥⎥⎥⎥ [ ( x 0 ) 0 ( x 0 ) 1 ( x 0 ) 2 ⋯ ( x 0 ) n − 1 ( x 1 ) 0 ( x 1 ) 1 ( x 1 ) 2 ⋯ ( x 1 ) n − 1 ( x 2 ) 0 ( x 2 ) 1 ( x 2 ) 2 ⋯ ( x 2 ) n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ ( x n − 1 ) 0 ( x n − 1 ) 1 ( x n − 1 ) 2 ⋯ ( x n − 1 ) n − 1 ] ∗ [ a 0 a 1 a 2 ⋮ a n − 1 ] = [ y 0 y 1 y 2 ⋮ y n − 1 ]

因为我们代入的 x0,x1,x2...xn−1 x 0 , x 1 , x 2 . . . x n − 1 分别是 ω0n,ω1nω2n...ωn−1n ω n 0 , ω n 1 ω n 2 . . . ω n n − 1 .
矩阵就变成了

⎡⎣⎢⎢⎢⎢⎢⎢(ω0n)0(ω1n)0(ω2n)0⋮(ωn−1n)0(ω0n)1(ω1n)1(ω2n)1⋮(ωn−1n)1(ω0n)2(ω1n)2(ω2n)2⋮(ωn−1n)2⋯⋯⋯⋱⋯(ω0n)n−1(ω1n)n−1(ω2n)n−1⋮(ωn−1n)n−1⎤⎦⎥⎥⎥⎥⎥⎥∗⎡⎣⎢⎢⎢⎢⎢⎢a0a1a2⋮an−1⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢y0y1y2⋮yn−1⎤⎦⎥⎥⎥⎥⎥⎥ [ ( ω n 0 ) 0 ( ω n 0 ) 1 ( ω n 0 ) 2 ⋯ ( ω n 0 ) n − 1 ( ω n 1 ) 0 ( ω n 1 ) 1 ( ω n 1 ) 2 ⋯ ( ω n 1 ) n − 1 ( ω n 2 ) 0 ( ω n 2 ) 1 ( ω n 2 ) 2 ⋯ ( ω n 2 ) n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ ( ω n n − 1 ) 0 ( ω n n − 1 ) 1 ( ω n n − 1 ) 2 ⋯ ( ω n n − 1 ) n − 1 ] ∗ [ a 0 a 1 a 2 ⋮ a n − 1 ] = [ y 0 y 1 y 2 ⋮ y n − 1 ]

设这个矩阵为

A∗B=C A ∗ B = C

在刚才的变换中,我们已知 B B 向量,然后通过分治算法求得 C C 向量.
现在我们通过 O(n) O ( n ) 时间的乘法得到新的 C C 向量,也就是新的点值表示,我们要重新求回原来的 B B 向量,怎么办
考虑逆矩阵.

A−1∗A∗B=A−1∗C A − 1 ∗ A ∗ B = A − 1 ∗ C

B=A−1∗C B = A − 1 ∗ C

我们只要求出 A A 的逆矩阵就可以求出 B B 向量了
A A 的逆矩阵并不好求,我们只需要知道它是什么就好了

A A 矩阵是一个特殊的范德蒙德矩阵,范德蒙德矩阵就是指每一行的元素为一个等比数列.
对于这个矩阵,我们有

A−1=1n∗A⎯⎯⎯⎯ A − 1 = 1 n ∗ A ¯

其中 A⎯⎯⎯⎯ A ¯ 是 A的共轭矩阵 A 的 共 轭 矩 阵 ,共轭矩阵就是指矩阵内的所有元素都取共轭复数得到的矩阵.
具体证明最后再讲.

有了这个性质我们重新看看最开始的式子:

B=A−1∗CB=1n∗A⎯⎯⎯⎯∗C B = A − 1 ∗ C B = 1 n ∗ A ¯ ∗ C

⎡⎣⎢⎢⎢⎢⎢⎢a0a1a2⋮an−1⎤⎦⎥⎥⎥⎥⎥⎥=1n⎡⎣⎢⎢⎢⎢⎢⎢(ω0n)0(ω−1n)0(ω−2n)0⋮(ω−(n−1)n)0(ω0n)1(ω−1n)1(ω−2n)1⋮(ω−(n−1)n)1(ω0n)2(ω−1n)2(ω−2n)2⋮(ω−(n−1)n)2⋯⋯⋯⋱⋯(ω0n)n−1(ω−1n)n−1(ω−2n)n−1⋮(ω−(n−1)n)n−1⎤⎦⎥⎥⎥⎥⎥⎥∗⎡⎣⎢⎢⎢⎢⎢⎢y0y1y2⋮yn−1⎤⎦⎥⎥⎥⎥⎥⎥ [ a 0 a 1 a 2 ⋮ a n − 1 ] = 1 n [ ( ω n 0 ) 0 ( ω n 0 ) 1 ( ω n 0 ) 2 ⋯ ( ω n 0 ) n − 1 ( ω n − 1 ) 0 ( ω n − 1 ) 1 ( ω n − 1 ) 2 ⋯ ( ω n − 1 ) n − 1 ( ω n − 2 ) 0 ( ω n − 2 ) 1 ( ω n − 2 ) 2 ⋯ ( ω n − 2 ) n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ ( ω n − ( n − 1 ) ) 0 ( ω n − ( n − 1 ) ) 1 ( ω n − ( n − 1 ) ) 2 ⋯ ( ω n − ( n − 1 ) ) n − 1 ] ∗ [ y 0 y 1 y 2 ⋮ y n − 1 ]

是不是很神奇?原来的只要将我们分治的时候代入的 ωxn ω n x 换成 ω−xn ω n − x 就可以求出 B B 向量,也就是系数表示了.

---

现在证明

A−1=1n∗A⎯⎯⎯⎯ A − 1 = 1 n ∗ A ¯

设

1n∗A⎯⎯⎯⎯∗A=C 1 n ∗ A ¯ ∗ A = C

我们就是要证明 C=U C = U , U U 是单位矩阵

1n⎡⎣⎢⎢⎢⎢⎢⎢(ω0n)0(ω1n)0(ω2n)0⋮(ωn−1n)0(ω0n)1(ω1n)1(ω2n)1⋮(ωn−1n)1(ω0n)2(ω1n)2(ω2n)2⋮(ωn−1n)2⋯⋯⋯⋱⋯(ω0n)n−1(ω1n)n−1(ω2n)n−1⋮(ωn−1n)n−1⎤⎦⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢(ω0n)0(ω−1n)0(ω−2n)0⋮(ω−(n−1)n)0(ω0n)1(ω−1n)1(ω−2n)1⋮(ω−(n−1)n)1(ω0n)2(ω−1n)2(ω−2n)2⋮(ω−(n−1)n)2⋯⋯⋯⋱⋯(ω0n)n−1(ω−1n)n−1(ω−2n)n−1⋮(ω−(n−1)n)n−1⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢100⋮0010⋮0001⋮0⋯⋯⋯⋱⋯000⋮1⎤⎦⎥⎥⎥⎥⎥⎥ 1 n [ ( ω n 0 ) 0 ( ω n 0 ) 1 ( ω n 0 ) 2 ⋯ ( ω n 0 ) n − 1 ( ω n 1 ) 0 ( ω n 1 ) 1 ( ω n 1 ) 2 ⋯ ( ω n 1 ) n − 1 ( ω n 2 ) 0 ( ω n 2 ) 1 ( ω n 2 ) 2 ⋯ ( ω n 2 ) n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ ( ω n n − 1 ) 0 ( ω n n − 1 ) 1 ( ω n n − 1 ) 2 ⋯ ( ω n n − 1 ) n − 1 ] [ ( ω n 0 ) 0 ( ω n 0 ) 1 ( ω n 0 ) 2 ⋯ ( ω n 0 ) n − 1 ( ω n − 1 ) 0 ( ω n − 1 ) 1 ( ω n − 1 ) 2 ⋯ ( ω n − 1 ) n − 1 ( ω n − 2 ) 0 ( ω n − 2 ) 1 ( ω n − 2 ) 2 ⋯ ( ω n − 2 ) n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ ( ω n − ( n − 1 ) ) 0 ( ω n − ( n − 1 ) ) 1 ( ω n − ( n − 1 ) ) 2 ⋯ ( ω n − ( n − 1 ) ) n − 1 ] = [ 1 0 0 ⋯ 0 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 1 ]

Ci,j=1n∑n−1k=0Ai,k∗A⎯⎯⎯⎯k,j C i , j = 1 n ∑ k = 0 n − 1 A i , k ∗ A ¯ k , j

当 i=j i = j 时

Ai,k∗A⎯⎯⎯⎯k,i=1 A i , k ∗ A ¯ k , i = 1 ,根据棣莫弗定理,模长为一的两个共轭复数相乘以后等于1.

Ci,j=1n∑n−1k=01=1 C i , j = 1 n ∑ k = 0 n − 1 1 = 1

当 i≠j i ≠ j 时

Ci,j=1n∑n−1k=0Ai,k∗A⎯⎯⎯⎯k,j C i , j = 1 n ∑ k = 0 n − 1 A i , k ∗ A ¯ k , j

=1n∑n−1k=0(ωin)k∗(ω−kn)j = 1 n ∑ k = 0 n − 1 ( ω n i ) k ∗ ( ω n − k ) j

=1n∑n−1k=0(ωi−jn)k = 1 n ∑ k = 0 n − 1 ( ω n i − j ) k

ωi−jn ω n i − j 可以视为常数项,就变成了等比数列求和公式.

=1nωi−jn[1−(ωi−jn)n]1−ωi−j = 1 n ω n i − j [ 1 − ( ω n i − j ) n ] 1 − ω i − j

因为 (ωi−jn)n=1,i!=j ( ω n i − j ) n = 1 , i ! = j .

Ci,j=0 C i , j = 0 .

所以 C=U C = U 就是我们要证的单位矩阵.

---

对刚才的几个操作取个名字
系数到点值的转换操作叫做DFT(离散傅立叶变换)
点值到系数的转换叫IDFT(离散傅立叶逆变换)
总的三步操作合起来叫做FFT(快速傅立叶变换)

最后看一看代码
洛谷上有模板题.

#include
#include
#include
#include
using namespace std;
#define maxn 5000010
const double Pi=acos(-1.0);
inline int read(){
    int ret=0,ff=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') ff=-ff;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        ret=ret*10+ch-'0';
        ch=getchar();
    }
    return ret*ff;
}
int lim=1,l=0;
int r[maxn];
struct Complex{
    double x,y;
    Complex(double _x=0,double _y=0){x=_x,y=_y;}
    Complex operator+(Complex t){ return Complex(x+t.x,y+t.y);}
    Complex operator-(Complex t){ return Complex(x-t.x,y-t.y);}
    Complex operator*(Complex t){ return Complex(x*t.x-y*t.y,x*t.y+y*t.x);}
}a[maxn],b[maxn];
void fft(Complex *A,int op){
    for(int i=0;iif(i//用之前的r[i]存的顺序对A重新排列
    for(int Mid=1;Mid1){
    //披着倍增外套的分治
        Complex Wn(cos(Pi/Mid),op*sin(Pi/Mid));//因为Mid是我们枚举的中点,本来就是要求区间的2倍,所以把2约掉
        for(int R=Mid<<1,j=0;j1,0);
            for(int k=j;kint main(){
//  freopen("mod.in","r",stdin);
    int n=read(),m=read();
    for(int i=0;i<=n;++i) a[i].x=read();
    for(int j=0;j<=m;++j) b[j].x=read();
    while(lim<=n+m) lim<<=1,++l;
    for(int i=0;i>1]>>1)|((i&1)<<(l-1));
    //这一步就是二进制的转置部分,r[i]表示i的二进制转置,比如说r[6(110)]=3(011)
    //r[i]由r[i/2]递推得来,对比i和i/2的二进制规律,我们发现i=(i>>1)<<1|(i&1)
    //因为r[i]是i的倒序,所以也应该是倒序递推
    fft(a,1),fft(b,1);
    for(int i=0;i1);
    for(int i=0;i<=n+m;++i) printf("%d ",int(a[i].x/lim+0.5));
    return 0;
}