ROC及AUC计算方法及原理
1.非均衡分类问题
在大多数情况下不同类别的分类代价并不相等,即将样本分类为正例或反例的代价是不能相提并论的。例如在垃圾邮件过滤中,我们希望重要的邮件永远不要被误判为垃圾邮件,还有在癌症检测中,宁愿误判也不漏判。在这种情况下,仅仅使用分类错误率来度量是不充分的,这样的度量错误掩盖了样本如何被错分的事实。所以,在分类中,当某个类别的重要性高于其他类别时,可以使用Precison和Recall多个比分类错误率更好的新指标。
Precison(查准率):预测为正例的样本中真正正例的比例。
Recall(召回率):真正为正例的样本有多少被预测出来。
可见,我们可以根据我们最终的目标来选择度量指标。例如,在癌症检测中,我们希望选择Recall较高的模型(有病为正例)。而在垃圾邮件过滤中,我们希望选择Precison较高的模型。但是我们很容易构造一个高查准率或高召回率的分类器,但是很难保证两者同时成立。构建一个同时使两者很大的分类器是具有挑战性的。
2.ROC曲线
ROC是一个用于度量分类中的非均衡性的工具,ROC曲线及AUC常被用来评价一个二值分类器的优劣。
既然已经有了这么多的评价指标,为什么还要使用ROC与AUC呢?
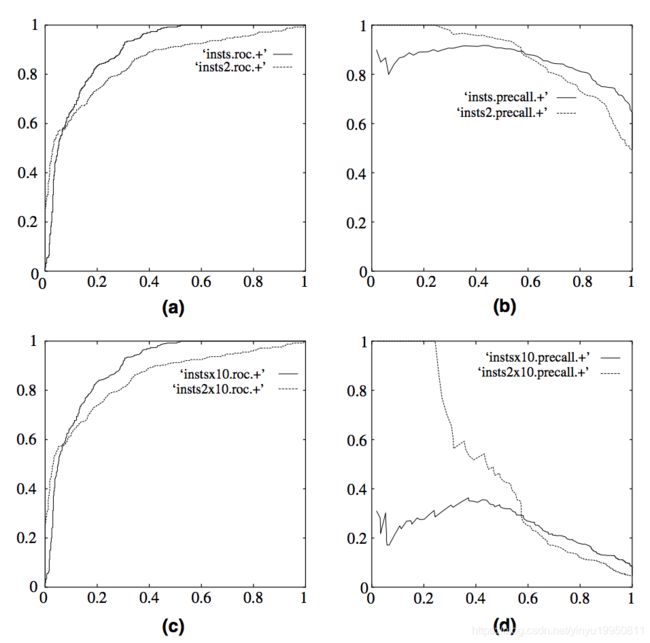
因为ROC曲线有一个很好的特征:在实际的数据集中经常会出现类别不平衡现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间而变化。而在这种情况下,ROC曲线能够保持不变。下图是ROC曲线和Precison-Recall曲线的对比:
在上图中,a和c为ROC曲线,b和d为Precison和Recall曲线。a和b展示的是在原始测试集(正负样本平衡)的结果,c和d是将测试集中负样本的数量变为原来的10倍后分类器的结果。可以看出,曲线基本保持不变,而Precison和Recall变化较大。
2.2 ROC曲线的定义(Receiver Operating Characteristic)
ROC可以用来比较不同分类器的相关性能。
如图是一个ROC曲线的实例:
其中横坐标为FPR(False positive rate 假阳率),纵坐标为真阳率TPR(True postive rate)。
FPR:所有负例中有多少被预测为正例; TPR:有多少真正的正例被预测出来;
ROC 描绘了两者的相对权衡:
- benefits(true postives)
- costs(false positives)
下图给出了Precison,Recall, FPR,TPR的定义:
| predicted Postive | predicted Negative | |
| real Postive | TP | FN |
| real Negative | FP | TN |
F-measure: precison和recall的调和平均值。没有一个单个的度量可以告诉所有的信息,所以建议使用多个度量。
接下来我们考虑ROC曲线中的四个点和一条线。
1.(0,0):fp=tp=0 ,即所有样本都被预测为负样本;
2.(1,1):fp=tp=1,所有样本都被预测为正样本;
3.(1,0):fp=1,tp=0,所有正例都被预测为负例,而所有正例都没被预测出来,这时最糟糕的分类器,因为它成功的避开了所有正确答案。
4.(0,1):fp=0,tp=1,这是一个完美的分类器,它将所有样本都正确分类。
所以经过上述分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好,意味着分类器在假阳率很低的同时获得了很高的真阳率。
5. 虚线y=x:这条对角线熵的点其实代表的是一个采用随机猜测策略的分类器的结果。例如(0.5,0.5),表示对于一半的样本猜测其为正样本,另外一半样本为负样本。出现在右下角三角形中的任何分类器都比随机猜测更糟糕。因此,在ROC图中,此三角形通常为空。
3.AUC的含义
AUC(Area Under Curve) 被定义为ROC曲线下的面积,因为ROC曲线一般都处于y=x这条直线的上方,所以取值范围在0.5和1之间,使用AUC作为评价指标是因为ROC曲线在很多时候并不能清晰地说明哪个分类器的效果更好,而AUC作为一个数值,其值越大代表分类器效果更好。
AUC意味着什么?
The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.
首先AUC是一个概率值,当随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的分数将这个正样本排在负样本前面的概率就是AUC值。所以,AUC的值越大,当前的分类算法越有可能将正样本排在负样本值前面,既能够更好的分类。
4. ROC曲线的绘制
我们可以看出,对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR的结果,那么是如何得到整个ROC曲线的呢?
要想得到ROC曲线,我们就需要一组FPR和TPR的值。我们先来看Wikipedia上面对ROC曲线的定义:
“In signal detection theory, a receiver oprating characteristic(ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied.”
ROC曲线代表的是当“discriminative threshold“变化时分类器的性能、如何理解这里的“discriminative threshold”呢?
它代表的是分类器以多大的置信度将样本分类为正样本。分类器的一个重要功能”概率输出“,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本)。通过深入地了解各个分类器的内部机理,我们总能想办法得到一种概率输出。通常来说,是将一个实数范围通过某个变化映射到(0,1)区间。
假设我们已经得到了所有样本的概率输出(即属于正样本的概率),那么我们就可以通过改变”discrimination threshold“来绘制ROC曲线。
(许多分类器,例如决策树或者规则集合,被设计产生一个类别决策,即将每个样本预测为Y或N。当使用这样的离散分类器时,产生一个单个额confusion矩阵,对应于一个ROC点。而一些分类器,例如Naive Bayes,产生一个样本概率值,这样一个ranking/scoring分类器可以使用一个threshold来产生一个discrete(binary)分类器:如果分类器输出的概率大于threshold,分类器产生Y,否则产生N。每个不同的threshold值在ROC空间产生一个不同的点(对应于一个不同的confusion matrix)。)
具体过程如下所述:
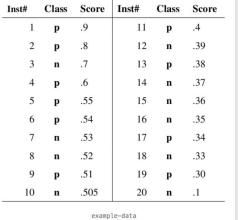
1.如图,我们根据每个测试样本属于正样本的概率值score从大到小排序。(图中class一栏代表每个测试样本的真正标签(p代表正样本,n代表负样本))
2.接着,我们从高到低,依次将score作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。
例如:对于第四个样本,其score值为0.6,那么score值大于等于0.6的样本1,2,3,4都被认为是正样本,而其他样本则被认为是负样本。
3.每次选取不同的score作为threshold,我们就可以得到一组FPR和TPR,即曲线上的一点。将这些(FPR,TPR)对连接起来,就可以得到完整的ROC曲线如下图。(当threshold取值越多,ROC曲线就越平滑)。
当我们将threshold设置为1和0时,即分别对应将所有样本划分为负样本和将所有样本划分为正样本,就可以的得到曲线上的(0,0)和(1,1)两点。
关于score值:分类器都会提供每个样例被判为阳性或者阴性的可信程度值,大多数分类器都能够做到这一点,但是在通常情况下,这些值会在最后输出离散分类标签之前被清除。例如,朴素贝叶斯能够提供一个可能值,在Logistic回归中输入到sigmoid函数中的是一个数值。在Adaboost和SVM中,都会计算一个数值然后输入到sign()函数中,所有的这些值都可以看做score,用于衡量给定分类器的预测强度。
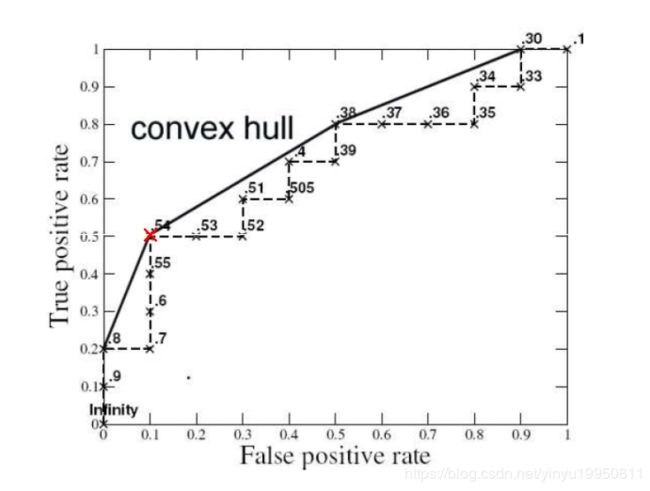
ROC点(0.1,0.5)产生了最高的准确率。注意到分类器的最好的准确率出现在threshold=0.54时,而不是我们认为的在类别平衡分布的threshold等于0.5处。
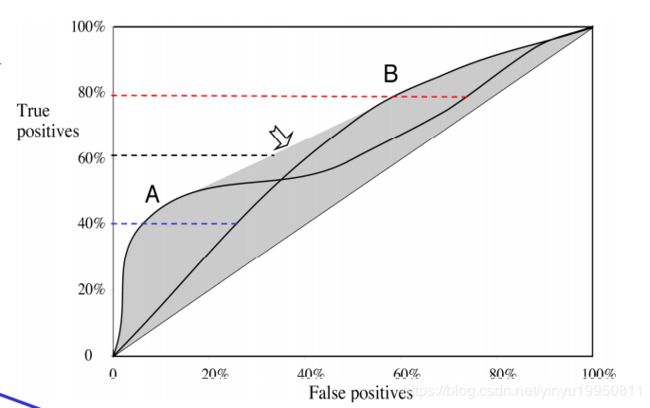
4.1 Convex Hull
阴影区域被称作两个曲线的convex hull。在选择分类器时总是应该根据convex hull的上边界进行操作。例如,如果你的目标只是覆盖40%的真阳性,你应该选择方法A,这样可以提供5%的更低的假阳性率相对于B来说。如果你的目标是覆盖80%的真阳性,你应该选择方法B,因为B的假阳性率为60%,与A相比更低。如果你的目标是覆盖60%的真阳性,那么你应该结合A和B。
5. 准确性的不足(代价敏感学习)
在金融检测中,如果将欺诈用户误判为优质客户,这样会给企业带来巨大损失。同样把病人误判为健康的人,会给病人带来生命威胁,这些问题都是代价敏感分类问题。即将样本误分类为正样本和将样本误分类为负样本的代价是不同的。然而,许多传统的分类算法假定分类代价都是相等的,分类的时候一般就考虑怎么使得分类模型的准确率更高,这样就可能忽视掉分类代价的问题。但是往往分类代价相比分类准确率具有更加重要的意义。正如上面的例子,欺诈用户和有病的人一般是小类别样本,将它们进行正确分类更为重要,如果将它们误分类将会产生严重的后果,我们的目标就是检查出这些异常。
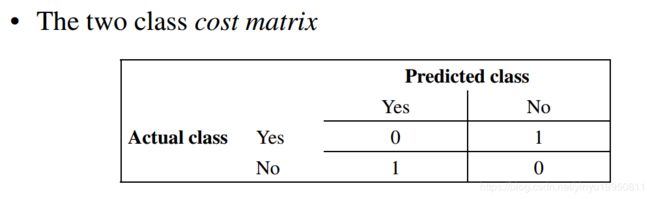
传统的分类算法不适合解决代价敏感的问题,这就需要研究能够解决代价敏感问题的分类方法,所以可以在传统分类方法中引入代价因子,运用代价敏感学习减少分类代价。成本矩阵![]() 表示将i类样本误分类为类j的代价。代价敏感分类就是为不同类型的错误分类不同的代价,使得分类时,高代价错误产生的数量和错误分类的代价总和最小。
表示将i类样本误分类为类j的代价。代价敏感分类就是为不同类型的错误分类不同的代价,使得分类时,高代价错误产生的数量和错误分类的代价总和最小。
基于损失的分类:
对于每个样本E,分类器计算![]() 和
和 ![]() ,分类器将样本分类为正例当:
,分类器将样本分类为正例当:
MetaCost(代价敏感学习):MetaCost是一种典型的集成学习算法,其核心思想是计算出每个训练样本额预测分类概率,再根据最优分类期望代价重标记原训练样本的类标号,得到新的训练集,然后在新的训练集上重新运行目标分类算法进行训练,从而实现代价敏感分类。
6. ROC曲线的python代码实现
def plotROC(predStrengths, classLabels):
cur=(0.0, 0.0)
numPosClass = np.sum(np.array(classLabels) == 1.0)
yStep = 1.0/numPosClass
xStep = 1.0/(len(classLabels)-numPosClass)
print(np.array(predStrengths.flatten()))
sortedIndicies = np.argsort(-np.array(predStrengths.flatten()))
print(sortedIndicies)
fig = plt.figure()
fig.clf()
ySum = 0.0
ax = plt.subplot(111)
for index in sortedIndicies:
if classLabels[index] == 1.0:
delY = yStep; delX=0
else:
delY = 0; delX = xStep
ySum += cur[1]
ax.plot([cur[0], cur[0]+delX], [cur[1], cur[1]+delY], c='b')
cur = (cur[0]+delX, cur[1]+delY)
print(cur)
ax.plot([0, 1], [0, 1], 'b--')
ax.axis([0, 1, 0, 1])
plt.xlabel('False Positve Rate')
plt.ylabel('True Postive Rate')
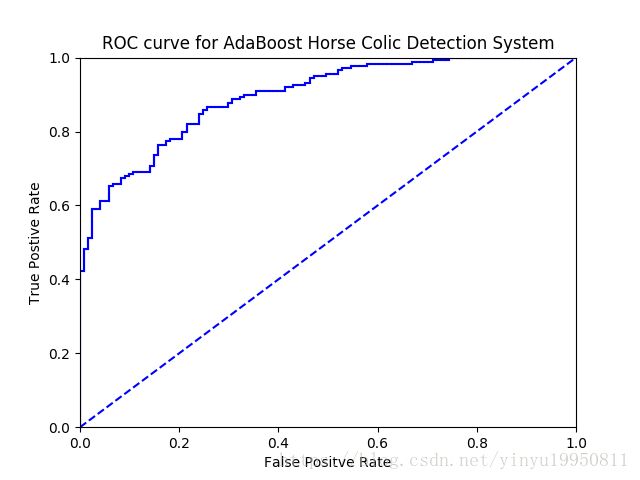
plt.title('ROC curve for AdaBoost Horse Colic Detection System')
ax.axis([0, 1, 0, 1])
plt.show()
print('the Area under the curve is:', ySum*xStep)代码解释:
上述程序中的函数有两个输入参数,第一个参数就代表的是score,代表的是分类器的预测强度。第二个参数是classLabels,即样本真实的类标签。首先创建一个浮点数二元组cur,将它初始化为(0.0,0.0),代表从坐标点(0.0,0.0)开始绘制ROC曲线。接着通过数组过滤的方式计算正例的数目,并将该值赋给numPosClas,该值确定了在y坐标轴上的步进数目。(因为y轴的含义是有多少正例被预测出来,所以它的长度为正例的数目),相应的,也可以得到x轴的步长。
接下来,我们将score从大到小排序得到排序索引,因为threshold是从大到小设置。所以最开始threshold为1.0,即所有样本都被预测为负例,因此是从点(0,0)开始绘制。当在循环中遍历坐标点时,每当得到一个类别为1的样本,那么就要沿着y轴增加一个步长,即增加真阳率。对于类别为0的样本,则沿着x轴增加一个步长,增加假阳率。一旦确定了是在哪个轴的方向熵进行移动的,就可以在当前点和新点之间画出一条线段,再更新坐标点cur。
(例如,对与样本点1,当前threshold为0.9,即score大于等于0.9的样本为正,小于为负,那么样本点1就被预测为正,而该样本的真实标签也为正,所以真阳率+1。同理,当遍历到样本3时,threshold设为0.7,此时样本3被预测为正例,但是该样本其实为负例,所以假阳率+1,代表又一个负样本被误判为正例。)
为了计算,我们需要对多个小矩形的面积进行累加。这些小矩形的宽度是xStep,因此我们可以对所有矩形的高度进行累加,所有高度的和随着x轴的每次移动而依次增加,然后再乘以xStep得到总面积。
运行结果: