详解概率图模型——有向图模型:贝叶斯网络
详解概率图模型——有向图模型:贝叶斯网络
- 详解概率图模型——有向图模型:贝叶斯网络
- 贝叶斯定理
- 条件概率
- 全概率公式
- 贝叶斯公式
- 贝叶斯网络
- 概念
- 实例:贝叶斯网络Student模型
- 概率模型图
- Python实现
详解概率图模型——有向图模型:贝叶斯网络
贝叶斯网络是机器学习中非常经典的算法之一,它能够根据已知的条件来估算出不确定的知识,应用范围非常的广泛。贝叶斯网络以贝叶斯公式为理论接触构建成了一个有向无环图,我们可以通过贝叶斯网络构建的图清晰的根据已有信息预测未来信息。
贝叶斯定理
条件概率
条件概率是指一个事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作在B条件下A的概率。

全概率公式
举例:
贝叶斯公式

P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
P(A)是A的先验概率或边缘概率。之所以称为”先验”是因为它不考虑任何B方面的因素。
P(B)是B的先验概率或边缘概率。
举例:
贝叶斯网络
概念
贝叶斯网络,由一个有**向无环图(DAG)和条件概率表(CPT)**组成。
贝叶斯网络通过一个有向无环图来表示一组随机变量跟它们的条件依赖关系。它通过条件概率分布来参数化。每一个结点都通过P(node|Pa(node))来参数化,Pa(node)表示网络中的父节点。
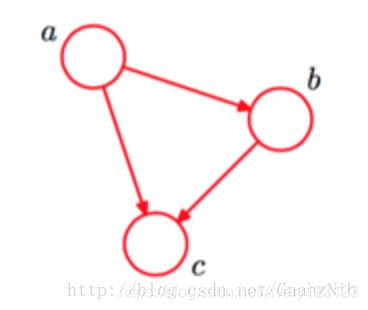
如图是一个简单的贝叶斯网络,其对应的全概率公式为:
较复杂的贝叶斯网络,其对应的全概率公式为
P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)

实例:贝叶斯网络Student模型
概率模型图
一个学生拥有成绩、课程难度、智力、SAT得分、推荐信等变量。通过一张有向无环图可以把这些变量的关系表示出来,可以想象成绩由课程难度和智力决定,SAT成绩由智力决定,而推荐信由成绩决定。该模型对应的概率图如下:

Python实现
from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
# 通过边来定义贝叶斯模型
model = BayesianModel([('D', 'G'), ('I', 'G'), ('G', 'L'), ('I', 'S')])
# 定义条件概率分布
cpd_d = TabularCPD(variable='D', variable_card=2, values=[[0.6, 0.4]])
cpd_i = TabularCPD(variable='I', variable_card=2, values=[[0.7, 0.3]])
# variable:变量
# variable_card:基数
# values:变量值
# evidence:
cpd_g = TabularCPD(variable='G', variable_card=3,
values=[[0.3, 0.05, 0.9, 0.5],
[0.4, 0.25, 0.08, 0.3],
[0.3, 0.7, 0.02, 0.2]],
evidence=['I', 'D'],
evidence_card=[2, 2])
cpd_l = TabularCPD(variable='L', variable_card=2,
values=[[0.1, 0.4, 0.99],
[0.9, 0.6, 0.01]],
evidence=['G'],
evidence_card=[3])
cpd_s = TabularCPD(variable='S', variable_card=2,
values=[[0.95, 0.2],
[0.05, 0.8]],
evidence=['I'],
evidence_card=[2])
# 将有向无环图与条件概率分布表关联
model.add_cpds(cpd_d, cpd_i, cpd_g, cpd_l, cpd_s)
# 验证模型:检查网络结构和CPD,并验证CPD是否正确定义和总和为1
model.check_model()
获取上述代码构建的概率图模型:
In[1]:model.get_cpds()
Out[1]:
[<TabularCPD representing P(D:2) at 0x10286e198>,
<TabularCPD representing P(I:2) at 0x10286e160>,
<TabularCPD representing P(G:3 | I:2, D:2) at 0x100d69710>,
<TabularCPD representing P(L:2 | G:3) at 0x10286e1d0>,
<TabularCPD representing P(S:2 | I:2) at 0x1093f6358>]
获取结点G的概率表:
In[2]:print(model.get_cpds('G'))
╒═════╤═════╤══════╤══════╤═════╕
│ I │ I_0 │ I_0 │ I_1 │ I_1 │
├─────┼─────┼──────┼──────┼─────┤
│ D │ D_0 │ D_1 │ D_0 │ D_1 │
├─────┼─────┼──────┼──────┼─────┤
│ G_0 │ 0.3 │ 0.05 │ 0.9 │ 0.5 │
├─────┼─────┼──────┼──────┼─────┤
│ G_1 │ 0.4 │ 0.25 │ 0.08 │ 0.3 │
├─────┼─────┼──────┼──────┼─────┤
│ G_2 │ 0.3 │ 0.7 │ 0.02 │ 0.2 │
╘═════╧═════╧══════╧══════╧═════╛
获取结点G的基数:
In[3]: model.get_cardinality('G')
Out[3]: 3
新数据节点值的预测跟计算条件概率非常相似,我们需要查询预测变量的其他全部特征。困难在于通过分布概率去代替更多可能的变量状态。
In[7]: infer.map_query('G')
Out[7]: {'G':