2019 Multi-University Training Contest 4 - Just an old puzzle
链接: http://acm.hdu.edu.cn/showproblem.php?pid=6620
Just an Old Puzzle
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 659 Accepted Submission(s): 425
Problem Description
You are given a 4 × 4 grid, which consists of 15 number cells and an empty cell.
All numbers are unique and ranged from 1 to 15.
In this board, the cells which are adjacent with the empty cell can move to the empty cell.
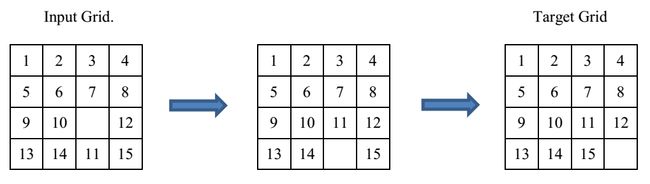
Your task is to make the input grid to the target grid shown in the figure below.
In the following example (sample input), you can get the target grid in two moves.
Input
The first line contains an integer T (1 <= T <= 10^5) denoting the number of test cases.
Each test case consists of four lines each containing four space-separated integers, denoting the input grid. 0 indicates the empty cell.
Output
For each test case, you have to print the answer in one line.
If you can’t get the target grid within 120 moves, then print 'No', else print 'Yes'.
Sample Input
2
1 2 3 4
5 6 7 8
9 10 0 12
13 14 11 15
1 2 3 4
5 6 7 8
9 10 11 12
13 15 14 0
Sample Output
Yes
No
题意:移动16宫格变成上图第三个宫格的样子,如果可以在120步之内还原,则输出 "YES",否则输出"NO" ;
在网上找到的板子,然后修修改改.....
正解是: 跟两种局面下逆序对的奇偶性和行差的奇偶性有关;;;
把这个东西拉成一个序列,发现空格上下交换,会改变逆序对数量的就行
看看这个空格所在的行号和逆序对的奇偶性就可以了
建议参考博客: https://blog.csdn.net/weixin_39708759/article/details/98043081
https://www.cnblogs.com/heyuhhh/p/11281642.html
AC代码:
#include
#include
#include
using namespace std;
#include
#define ll long long
const int Max = 4;
int a[4][2] = {0,-1,1,0,0,1,-1,0};
int goal[16][2]= {{3,3},{0,0},{0,1},{0,2},{0,3},{1,0},{1,1},{1,2},{1,3},{2,0},{2,1},{2,2},{2,3},{3,0},{3,1},{3,2}};
// 目标状态的数字所在位置
int mpp[Max][Max],mpp2[Max*Max];
int ffff;
int flag = 0,limit,Mi;
// 曼哈顿距离为 所有的数字要走到目标状态,最少要和0换的次数;
int ddd(int mpp[Max][Max]) {
int i,j;
int sum = 0;
for(i = 0; i<4; i++) {
for(j = 0; j<4; j++) {
if(mpp[i][j]!=0) //判断曼哈顿距离不能判断0;
sum += abs(i-goal[mpp[i][j]][0])+abs(j - goal[mpp[i][j]][1]);
}
}
return sum;
}
int nix(int mpp2[Max*Max]) {
int i,j;
int x,y;
int sum = 0;
for(i =0; i
y = i/4;
x = i%4;
continue;
}
for(j = i+1; j
if(mpp2[i]>mpp2[j])
sum++;
}
}
return sum;
}
void dfs(int y,int x,int len,int f) { // x,y当前0的坐标 len 为已经走了几步了;
// f为当上一次的搜索方向 为了不回搜,
if(len > 120) {
printf("SDS\n");
return;
}
if(ffff) {
return;
}
int d = ddd(mpp);
if(flag) return;
if(len<=limit) {
if(d==0) {
flag = 1;
Mi = len;
if(len <= 120) {
ffff = 1;
}
return ;
}
if(len==limit) return;
}
for(int i = 0; i<4; i++) {
int tx = x + a[i][0];
int ty = y + a[i][1];
if(tx>=0&&ty>=0&&ty<4&&tx<4&&((f==-1)||i!=(f+2)%4)) {
swap(mpp[y][x],mpp[ty][tx]);
if(len+ddd(mpp)<=limit) { // IDA* 减值,当前走的步数 加上 当前状态到达标状态的最小步数,
// 要小于等于 当前枚举到的最小的 从起始状态到达目标状态的步数,不能超过;
dfs(ty,tx,len+1,i);
if(flag) return ;
}
swap(mpp[y][x],mpp[ty][tx]);
}
}
}
int main() {
int i,j;
int t;
while(~scanf("%d", &t)) {
while(t--) {
ffff = 0;
scanf("%d",&mpp2[0]);
int y,x;
mpp[0][0] = mpp2[0];
if(mpp2[0]==0) {
y = 0;
x = 0;
}
for(i = 1; i
mpp[i/4][i%4] = mpp2[i];
if(mpp2[i]==0) {
y = i/4;
x = i%4;
}
}
int k = abs(y-goal[0][0]);//+abs(x-goal[0][0]);
int pp = nix(mpp2);
int f = 1;
if((pp+k)%2!=0)
f = 0;
if(!f) {
printf("No\n");
continue; //因为题意说过了,不会有不会到达的这种情况,但是我还是判断了
}
flag = 0;
limit = ddd(mpp); // 当前要达到目标状态的最小步数;
// printf("%d\n", limit);
// while(!flag&&limit<=55)
// {
// dfs(y,x,0,-1);
// if(!flag)
// limit ++; // 枚举最小步数;
// }
// if(flag){
if(limit <= 120)
printf("Yes\n");
else
printf("No\n");
// }
}
}
return 0;
}