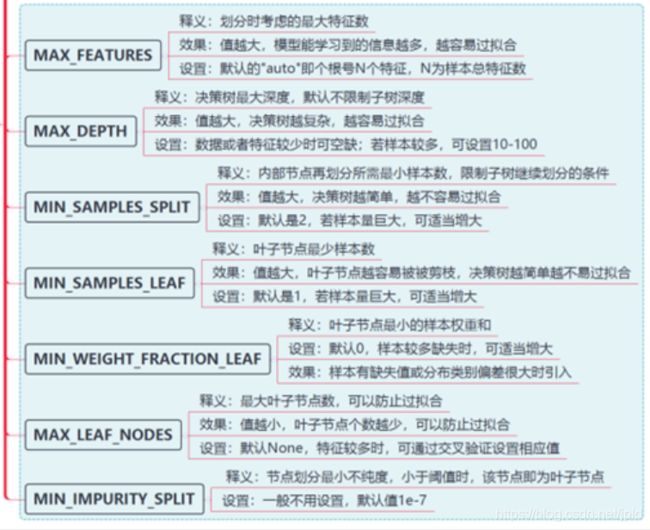
100天搞定机器学习|Day57 Adaboost知识手册(理论篇)
Boosting算法
Boosting是一种用来提高弱分类器准确度的算法,是将“弱学习算法“提升为“强学习算法”的过程,主要思想是“三个臭皮匠顶个诸葛亮”。一般来说,找到弱学习算法要相对容易一些,然后通过反复学习得到一系列弱分类器,组合这些弱分类器得到一个强分类器。
Boosting算法要涉及到两个部分,加法模型和前向分步算法。加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下:$$FM(x;P)=sum{m=1}^nbetamh(x;am)$$其中,$h(x;am)$就是一个个的弱分类器,$am$是弱分类器学习到的最优参数,$betam$就是弱学习在强分类器中所占比重,$P$是所有$alpham$和$beta_m$的组合。这些弱分类器线性相加组成强分类器。
前向分步就是说在训练过程中,下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是可以写成这样的形式:$$Fm (x)=F{m-1}(x) betamhm (x;a_m)$$
Adaboost基本概念
AdaBoost是典型的Boosting算法,属于Boosting家族的一员。 对于AdaBoost,我们要搞清楚两点:
对于AdaBoost,我们要搞清楚两点:
1、每一次迭代的弱学习$h(x;a_m)$有何不一样,如何学习?
2、弱分类器权值$beta_m$如何确定?
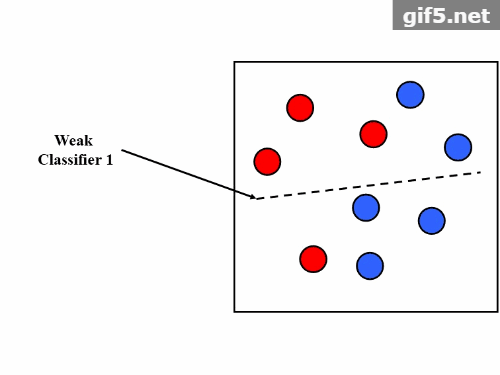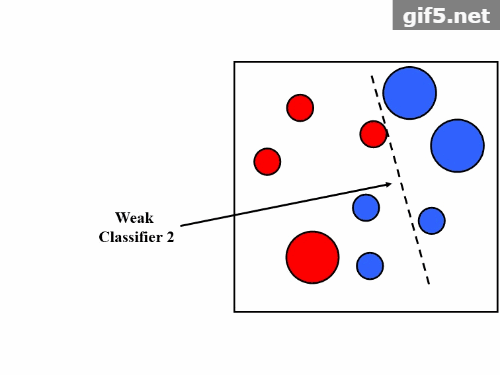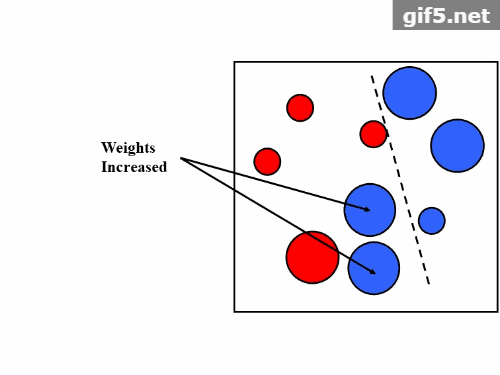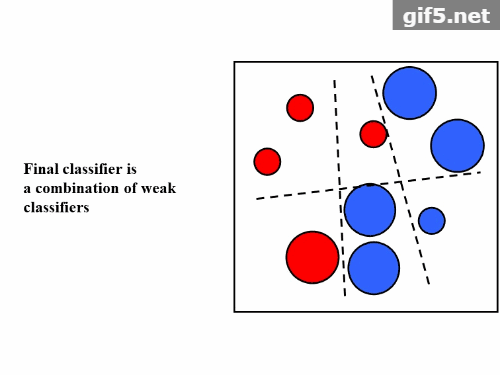
第一个问题,AdaBoost的做法是,提高那些被前一轮弱分类器错分类样本的权值,而降低那些被正确分类样本的权值。这样一来,那些没有得到正确分类的数据,由于其权值加大而受到后一轮的弱分类器的更大关注。于是,分类问题被一系列的弱分类器“分而治之”。
第二个问题,即弱分类器的组合,AdaBoost采取加权多数表决的方法。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。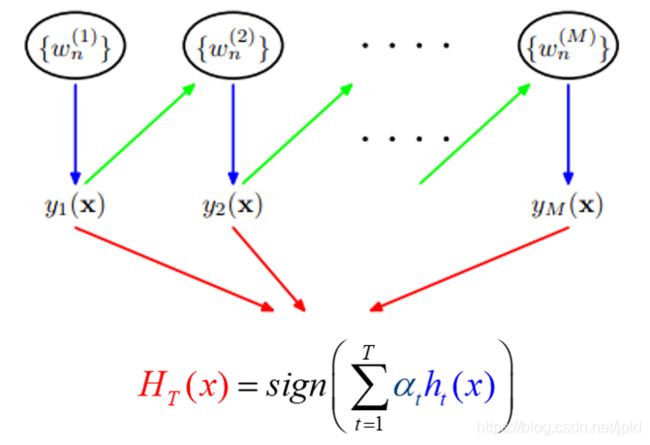
Adaboost算法流程-分类
输入:训练数据集$T={(x1,y1),(x2,y2),...,(xN,yN)}$,其中,$xi∈X?R^n$,$yi∈Y={-1,1}$,迭代次数$M$
1.初始化训练样本的权值分布:
$$begin{aligned}D1=(w{1,1},w{1,2},…,w{1,i}),\w_{1,i}=frac{1}{N},i=1,2,…,Nend{aligned}$$
2.对于$m=1,2,…,M$
(a) 使用具有权值分布$Dm$的训练数据集进行学习,得到弱分类器$Gm (x)$
(b) 计算$Gm(x)$在训练数据集上的分类误差率:$$em=sum{i=1}^Nw{m,i} I(Gm (xi )≠y_i )$$(c) 计算$Gm (x)$在强分类器中所占的权重:$$alpham=frac{1}{2}log frac{1-em}{em} $$(d) 更新训练数据集的权值分布(这里,(z_m)是归一化因子,为了使样本的概率分布和为1):$$w{m 1,i}=frac{w{m,i}}{zm}exp?(-alpham yi Gm (x_i )),i=1,2,…,10$$$$zm=sum{i=1}^Nw{m,i}exp?(-alpham yi Gm (x_i ))$$3.得到最终分类器:$$F(x)=sign(sum{i=1}^Nalpham G_m (x))$$
公式推导
假设已经经过$m-1$轮迭代,得到$F_{m-1} (x)$,根据前向分步,我们可以得到:$$Fm (x)=F{m-1} (x) alpham Gm (x)$$我们已经知道AdaBoost是采用指数损失,由此可以得到损失函数:$$begin{aligned}Loss=&sum{i=1}^Nexp?(-yi Fm (xi ))\=&sum{i=1}^Nexp?(-yi (F{m-1} (xi ) alpham Gm (x_i )))end{aligned}$$这时候,$F_{m-1}(x)$是已知的,可以作为常量移到前面去:$$Loss=sum{i=1}^Nwidetilde{w{m,i}} exp?(-yi alpham Gm (xi ))$$其中,$widetilde{w{m,i}}=exp?(-yi (F_{m-1} (x)))$ 就是每轮迭代的样本权重!依赖于前一轮的迭代重分配。再化简一下:$$begin{aligned}widetilde{w{m,i}}=&exp?(-yi (F{m-1} (xi ) alpha{m-1} G{m-1} (xi )))\=&widetilde{w{m-1,i}} exp?(-yi alpha{m-1} G{m-1} (xi ))end{aligned}$$继续化简Loss:$$begin{aligned}Loss=sum{yi=Gm(xi)}widetilde{w{m,i}} exp(-alpham) sum{yi≠Gm(xi)}widetilde{w{m,i}} exp?(alpham)\=sum{i=1}^Nwidetilde{w{m,i}}(frac{sum{yi=Gm(xi)}widetilde{w{m,i}}}{sum{i=1}^Nwidetilde{w{m,i}}}exp(-alpham) frac{sum{yi≠Gm(xi)}widetilde{w{m,i}}}{sum{i=1}^Nwidetilde{w{m,i}}}exp(alpham))end{aligned}$$
其中$frac{sum{yi≠Gm(xi)}widetilde{w{m,i}}}{sum{i=1}^Nwidetilde{w{m,i}}}$就是分类误差率$em$所以$Loss=sum{i=1}^Nwidetilde{w{m,i}}exp?(-alpham) em exp?(alpha_m))$这样我们就得到了化简之后的损失函数对$alpham$求偏导令$frac{?Loss}{?alpham }=0$得到:$$alpham=frac{1}{2}logfrac{1-em}{e_m}$$
AdaBoost实例
《统计学习方法》上面有个小例子,可以用来加深印象有如下的训练样本,我们需要构建强分类器对其进行分类。x是特征,y是标签。
 令权值分布$D1=(w{1,1},w{1,2},…,w{1,10} )$假设一开始的权值分布是均匀分布:$w_{1,i}=0.1,i=1,2,…,10$现在开始训练第一个弱分类器。我们发现阈值取2.5时分类误差率最低,得到弱分类器为:$$G_1(x)=begin{cases}1,& text{x<2.5} \-1,& text{x>2.5}end{cases}$$当然,也可以用别的弱分类器,只要误差率最低即可。这里为了方便,用了分段函数。得到了分类误差率$e_1=0.3$
令权值分布$D1=(w{1,1},w{1,2},…,w{1,10} )$假设一开始的权值分布是均匀分布:$w_{1,i}=0.1,i=1,2,…,10$现在开始训练第一个弱分类器。我们发现阈值取2.5时分类误差率最低,得到弱分类器为:$$G_1(x)=begin{cases}1,& text{x<2.5} \-1,& text{x>2.5}end{cases}$$当然,也可以用别的弱分类器,只要误差率最低即可。这里为了方便,用了分段函数。得到了分类误差率$e_1=0.3$
第二步计算$G1 (x)$在强分类器中的系数$alpha1=frac{1}{2} logfrac{ 1-e1}{e1}=0.4236$
第三步更新样本的权值分布,用于下一轮迭代训练。由公式:$$w{2,i}=frac{w{1,i}}{z1}exp?(-alpha1 yi G1 (x_i )),i=1,2,…,10$$得到新的权值分布,从各0.1变成了:$D_2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)$可以看出,被分类正确的样本权值减小了,被错误分类的样本权值提高了。
第四步得到第一轮迭代的强分类器:$$sign(F1 (x))=sign(0.4236G1 (x))$$以此类推,经过第二轮……第N轮,迭代多次直至得到最终的强分类器。迭代范围可以自己定义,比如限定收敛阈值,分类误差率小于某一个值就停止迭代,比如限定迭代次数,迭代1000次停止。这里数据简单,在第3轮迭代时,得到强分类器:$$sign(F3 (x))=sign(0.4236G1 (x) 0.6496G2 (x) 0.7514G3 (x))$$的分类误差率为0,结束迭代。
$F(x)=sign(F_3 (x))$就是最终的强分类器。
Adaboost参数详解
我们直接使用sklearn.ensemble中的AdaBoostRegressor和AdaBoostClassifier,两者大部分框架参数是相同的:
AdaBoostRegressor
class sklearn.ensemble.AdaBoostRegressor
(base_estimator=None, n_estimators=50,
learning_rate=1.0, loss=’linear’, random_state=None)AdaBoostClassifier
class sklearn.ensemble.AdaBoostClassifier
(base_estimator=None, n_estimators=50,
learning_rate=1.0, algorithm=’SAMME.R’, random_state=None)参数
1)baseestimator:AdaBoostClassifier和AdaBoostRegressor都有,即我们的弱分类学习器或者弱回归学习器。理论上可以选择任何一个分类或者回归学习器,不过需要支持样本权重。我们常用的一般是CART决策树或者神经网络MLP。默认是决策树,即AdaBoostClassifier默认使用CART分类树DecisionTreeClassifier,而AdaBoostRegressor默认使用CART回归树DecisionTreeRegressor。另外有一个要注意的点是,如果我们选择的AdaBoostClassifier算法是SAMME.R,则我们的弱分类学习器还需要支持概率预测,也就是在scikit-learn中弱分类学习器对应的预测方法除了predict还需要有predictproba。
2)algorithm:这个参数只有AdaBoostClassifier有。主要原因是scikit-learn实现了两种Adaboost分类算法,SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量,SAMME使用了二元分类Adaboost算法的扩展,即用对样本集分类效果作为弱学习器权重,而SAMME.R使用了对样本集分类的预测概率大小来作为弱学习器权重。由于SAMME.R使用了概率度量的连续值,迭代一般比SAMME快,因此AdaBoostClassifier的默认算法algorithm的值也是SAMME.R。我们一般使用默认的SAMME.R就够了,但是要注意的是使用了SAMME.R, 则弱分类学习器参数base_estimator必须限制使用支持概率预测的分类器。SAMME算法则没有这个限制。
3)loss:这个参数只有AdaBoostRegressor有,Adaboost.R2算法需要用到。有线性‘linear’, 平方‘square’和指数 ‘exponential’三种选择, 默认是线性,一般使用线性就足够了,除非你怀疑这个参数导致拟合程度不好。
4)nestimators: AdaBoostClassifier和AdaBoostRegressor都有,就是我们的弱学习器的最大迭代次数,或者说最大的弱学习器的个数。一般来说nestimators太小,容易欠拟合,nestimators太大,又容易过拟合,一般选择一个适中的数值。默认是50。在实际调参的过程中,我们常常将nestimators和下面介绍的参数learning_rate一起考虑。
5)learningrate: AdaBoostClassifier和AdaBoostRegressor都有,即每个弱学习器的权重缩减系数ν,在原理篇的正则化章节我们也讲到了,加上了正则化项,我们的强学习器的迭代公式为$fk(x)=fk?1(x) ναkGk(x)$。ν的取值范围为0 estimators和learning_rate要一起调参。一般来说,可以从一个小一点的ν开始调参,默认是1。
SAMME.R算法流程
1.初始化样本权值:$$w_i=1/N,i=1,2,…,N$$2.Repeat for$m=1,2,…,M$
2.1 训练一个弱分类器,得到样本的类别预测概率分布$p_m(x)=P(y=1|x)∈[0,1]$
2.2 $fm(x)=frac{1}{2}logfrac{pm(x)}{1-p_m(x)}$
2.3 $wi=wiexp[-y_if_m(x_i)]$,同时,要进行归一化使得权重和为13.得到强分类模型:$sign{sum{m=1}^{M}fm(x)}$
DecisionTreeClassifier和DecisionTreeRegressor的弱学习器参数,以CART分类树为例,这里就和前文随机森林类似了。
方法
decision_function(X):返回决策函数值
fit(X,Y):在数据集(X,Y)上训练模型
get_parms():获取模型参数
predict(X):预测数据集X的结果
predictlogproba(X):预测数据集X的对数概率
predict_proba(X):预测数据集X的概率值
score(X,Y):输出数据集(X,Y)在模型上的准确率
stageddecisionfunction(X):返回每个基分类器的决策函数值
staged_predict(X):返回每个基分类器的预测数据集X的结果
stagedpredictproba(X):返回每个基分类器的预测数据集X的概率结果
staged_score(X, Y):返回每个基分类器的预测准确率。
Adaboost总结
Adaboost优点
1.可以使用各种方法构造子分类器,Adaboost算法提供的是框架
2.简单,不用做特征筛选
3.相比较于RF,更不用担心过拟合问题
Adaboost缺点
1.从wiki上介绍的来看,adaboost对于噪音数据和异常数据是十分敏感的。Boosting方法本身对噪声点异常点很敏感,因此在每次迭代时候会给噪声点较大的权重,这不是我们系统所期望的。
2.运行速度慢,凡是涉及迭代的基本上都无法采用并行计算,Adaboost是一种"串行"算法.所以GBDT(Gradient Boosting Decision Tree)也非常慢。
参考:
李航《统计学习方法》第8章 提升方法《Getting Started with Machine Learning》Jim Lianghttps://www.cnblogs.com/pinard/p/6136914.htmlhttps://www.cnblogs.com/ScorpioLu/p/8295990.htmlhttps://louisscorpio.github.io/2017/11/28/AdaBoost入门详解/https://ask.hellobi.com/blog/zhangjunhong0428/10361
本文由博客一文多发平台 OpenWrite 发布!