对MLP(BP神经网络)反向传播公式的理解
虽然用了很久的神经网络编程框架了(不过也隔了很长时间没接触),但反向传播公式怎么来的还是记不住。于是今天就手动推导了一下。
先附一张图
下面是一张反向传播公式图。第一个公式是计算最后一层误差,第二个公式是反向地推公式,第三四个是根据误差推导 b 和 W 的更新公式。
不过这几个公式其实是简化后的写法,真正的写法使用的是 雅克比矩阵,这个留到最后讨论一下。
(不过这个误差好像是对 zi 而不是 ai 的,而且用对z的求导表示误差似乎是业界通识,还是记它比较好。但我之后用 C 对 a 的导数表示要进行反向传播的误差,原理一样。只要知道了原理,推 z 的就不是难事)
预定义变量
(以下所有向量都为列向量)
对第 i 层网络,权重(weight)为 Wi,偏置(bias)为 bi,激活函数为 f(假设是softmax),输入为 a[i-1],输出为 ai,其中 (Wi*a[i-1]+bi) 习惯上称为 zi
a i = f ( W i a i − 1 + b i ) = f ( z i ) a_i = f(W_{i} a_{i-1}+b_i)=f(z_i) ai=f(Wiai−1+bi)=f(zi)
对于最后一层,输出为 a_last
a l a s t = N e u r a l N e t w o r k ( a 0 ) , 即 整 个 网 络 的 输 出 a_{last}=NeuralNetwork(a_0),即整个网络的输出 alast=NeuralNetwork(a0),即整个网络的输出
代价为 C(一个标量),标签为y,代价函数为 Cost(y,a_last)
C = C o s t ( y , a l a s t ) C=Cost(y,a_{last}) C=Cost(y,alast)
推导
根据下面两条,可以求出 C 对所有 a_i 的偏导数
C = ∂ C o s t ( y , a l a s t ) ∂ a l a s t 【 最 后 一 层 】 C= \frac{\partial{Cost(y,a_{last})}}{\partial{a_{last}}} 【最后一层】 C=∂alast∂Cost(y,alast)【最后一层】
∂ C ∂ a i − 1 = ∂ C ∂ a i ∂ a i ∂ z i ∂ z i ∂ a i − 1 = W T ( ∂ C ∂ a i ⊙ f ′ ( z i ) ) 【 已 知 ∂ C ∂ a i , 求 ∂ C ∂ a i − 1 】 \frac{\partial{C}}{\partial{a_{i-1}}} = \frac{\partial{C}}{\partial{a_{i}}} \frac{\partial{a_i}}{\partial{z_i}} \frac{\partial{z_i}}{\partial{a_{i-1}}} =W^{T} (\frac{\partial{C}}{\partial{a_{i}}} \odot f^{'}(z_i)) 【已知 \frac{\partial{C}}{\partial{a_{i}}} ,求 \frac{\partial{C}}{\partial{a_{i-1}}}】 ∂ai−1∂C=∂ai∂C∂zi∂ai∂ai−1∂zi=WT(∂ai∂C⊙f′(zi))【已知∂ai∂C,求∂ai−1∂C】
实际上这只是一种简化,之后会提到。简单记住公式就行,下面是两点技巧用于记住公式
-
注意上面公式中矩阵求导后的矩阵形状以及乘法顺序问题,要保证矩阵乘法规则成立,且最后结果向量要和 a[i-1] 维数一致。知道这点技巧后,即使对矩阵求导规则不熟练也能把乘的顺序猜出一二。
-
激活函数导数部分 f ′ ( z i ) f^{'}(z_i) f′(zi)采取的是“逐值相乘”( ⊙ \odot ⊙),这并不违和,因为计算 f ( W i a i − 1 + b i ) f(W_{i} a_{i-1}+b_i) f(Wiai−1+bi)时也是逐值计算的。
知道了 ∂ C ∂ a i \frac{\partial{C}}{\partial{a_{i}}} ∂ai∂C后,求 ∂ C ∂ W i \frac{\partial{C}}{\partial{W_{i}}} ∂Wi∂C和 ∂ C ∂ b i \frac{\partial{C}}{\partial{b_{i}}} ∂bi∂C就很容易了。
∂ C ∂ W i = ∂ C ∂ a i ∂ a i ∂ z i ∂ z i ∂ W i = ( ∂ C ∂ a i ⊙ f ′ ( z i ) ) a i − 1 T \frac{\partial{C}}{\partial{W_{i}}} = \frac{\partial{C}}{\partial{a_{i}}} \frac{\partial{a_{i}}}{\partial{z_{i}}} \frac{\partial{z_i}}{\partial{W_{i}}} = (\frac{\partial{C}}{\partial{a_{i}}} \odot f^{'}(z_i))a_{i-1}^T ∂Wi∂C=∂ai∂C∂zi∂ai∂Wi∂zi=(∂ai∂C⊙f′(zi))ai−1T
∂ C ∂ b i = ∂ C ∂ a i ∂ a i ∂ z i ∂ z i ∂ b i = ∂ C ∂ a i ⊙ f ′ ( z i ) \frac{\partial{C}}{\partial{b_{i}}} = \frac{\partial{C}}{\partial{a_{i}}} \frac{\partial{a_{i}}}{\partial{z_{i}}} \frac{\partial{z_i}}{\partial{b_{i}}} = \frac{\partial{C}}{\partial{a_{i}}} \odot f^{'}(z_i) ∂bi∂C=∂ai∂C∂zi∂ai∂bi∂zi=∂ai∂C⊙f′(zi)
使用
假设学习率为 lr(learning rate),目标是使得 C 最小化,则可按照下式更新参数:
W i : = W i − l r ∂ C ∂ W i b i : = b i − l r ∂ C ∂ b i W_i := W_i - lr \frac{\partial{C}}{\partial{W_{i}}} \\ b_i := b_i - lr \frac{\partial{C}}{\partial{b_{i}}} Wi:=Wi−lr∂Wi∂Cbi:=bi−lr∂bi∂C
不过实际写代码的时候,这个 lr 应该放哪呢?
其实 l r ∂ C ∂ W i lr\frac{\partial{C}}{\partial{W_{i}}} lr∂Wi∂C按照上面链式法则的思路可以写成 ( l r ∂ C ∂ a l a s t ) ∂ a l a s t ∂ W i (lr\frac{\partial{C}}{\partial{a_{last}}})\frac{\partial{a_{last}}}{\partial{W_{i}}} (lr∂alast∂C)∂Wi∂alast
也就说,只要计算了 ( l r ∂ C ∂ a l a s t ) (lr\frac{\partial{C}}{\partial{a_{last}}}) (lr∂alast∂C),lr 会随着反向传播影响到所有层,所以只要在最后结果上使用 lr 就行。
举个例子:
平 方 损 失 函 数 : C = C o s t ( y , a ) = ( y − a ) T ( y − a ) 平方损失函数: C = Cost(y,a) = (y-a)^{T}(y-a) 平方损失函数:C=Cost(y,a)=(y−a)T(y−a)
∂ C ∂ a = 2 ( y − a ) \frac{\partial{C}}{\partial{a}}=2(y-a) ∂a∂C=2(y−a)
则 Δ a = l r × 2 ( y − a ) , 这 个 2 在 编 程 的 时 候 可 以 不 用 管 则 \Delta a = lr\times2(y-a),这个2在编程的时候可以不用管 则Δa=lr×2(y−a),这个2在编程的时候可以不用管
W i : = W i − Δ a ∂ a ∂ W i b i : = b i − Δ a ∂ a ∂ b i W_i := W_i -\Delta a\frac{\partial{a}}{\partial{W_{i}}} \\ b_i := b_i - \Delta a\frac{\partial{a}}{\partial{b_{i}}} Wi:=Wi−Δa∂Wi∂abi:=bi−Δa∂bi∂a
为什么说之前推导的公式是被简化过的?
为什么说之前推导的公式是被简化过的?
回想一下之前的“推导过程”,那些矩阵求导之后出现的矩阵乘法顺序问题,以及“逐值相乘”(百度百科里说叫“哈达马积”:矩阵乘法)看起来相当别扭。我看了很多博客里没有关于这点的解释,好像从上一步跳到下一步是理所当然的。我以前就是被这一点所蒙蔽,从来没有真正理解那些公式的真正含义。
(╯°Д°)╯︵┻━┻
直到我看到这篇关于softmax的博客: Softmax函数及其导数
实际上向量对向量求导的结果是一个 雅克比矩阵(雅克比矩阵是导数的推广,非对角线上的元素表示的是一种耦合),由于 softmax 或者 relu 函数不存在 i项与j项 的耦合,求出来的雅可比矩阵一定是一个对角矩阵,是一种特殊情况,做矩阵乘法时候和上面说的逐值相乘结果一样。不如就写成一个一维向量,存矩阵对角线元素,不仅省内存,还能提高效率。所以 ∂ a i ∂ z i = f ′ ( z i ) \frac{\partial{a_i}}{\partial{z_i}}=f^{'}(z_i) ∂zi∂ai=f′(zi)在做运算的时候可以写成一维向量,而且这么一改,为了满足运算规则,很多地方都得改,甚至在公式里加了“哈达马积”—— 反正我看的一头雾水。
不过像 softmax 这种 i 项和所有项相关的存在耦合,这时候就得老老实实求出雅克比矩阵,并使用运算量很大的矩阵乘法,顶多找一些技巧优化效率。
如果使用雅克比矩阵表示的话,这些反向传播的公式推导过程会变得非常容易理解,因为只涉及到普通的矩阵加法与乘法(当然如果还老想着“哈达马积”那套公式可能绕不过来)。
这是 z = Wx, z 对 W 的导数。其中 z 是 T 维向量,x 是 N 维向量,W 是 NxT 维矩阵。把 W 按照主序展开成一维向量,z 对 W 进行求导就是一个 TxNT 的雅克比矩阵。
如果让我按照它来编程,肯定会慢的怀疑人生(╯°Д°)╯︵┻━┻,除非找到可以大幅简化的技巧。
简化对推导产生影响的例子
T 维向量对 N 维矩阵求导会得到 TxN 矩阵;T 维向量对 TxN 矩阵求导会得到 TxNT 矩阵。根据这两点来分析下这个公式:
dC/dW 是常量对矩阵求导,所以和 W 尺寸一样。所以乍看之下,没有任何问题。(下式中替换 a 位置的是 dz/dW)
∂ C ∂ W i = ∂ C ∂ z i ∂ z i ∂ W i \frac{\partial{C}}{\partial{W_{i}}} = \frac{\partial{C}}{\partial{z_{i}}} \frac{\partial{z_i}}{\partial{W_{i}}} ∂Wi∂C=∂zi∂C∂Wi∂zi
但是考虑到 ∂ z i ∂ W i \frac{\partial{z_i}}{\partial{W_{i}}} ∂Wi∂zi`或者 ∂ a i ∂ W i \frac{\partial{a_i}}{\partial{W_{i}}} ∂Wi∂ai是 TxNT 矩阵后,上面BP4公式就怎么都让人想不通了。
先按照 Softmax函数及其导数 中的思路想一下。
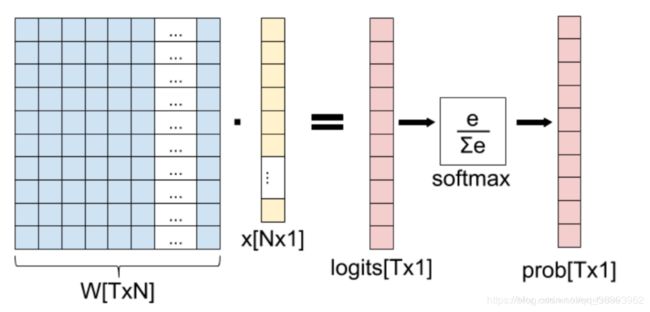
(其中S是激活函数softmax,g是矩阵乘法那一步)
Dg 是 TxNT 雅克比矩阵,而且Dg 大多数为0,仅当i=k时 D i j g k D_{ij}g{k} Dijgk不为0。如果把 [x1,x2,x3…xN]看成矩阵元素,记为 v,Dg 可以写成一个元素为行向量的对角矩阵,每个对角元素都是[x1,x2,x3…xN]。
v = [ x 1 x 2 ⋯ x N ] T D g = [ v T ⋱ v T ] v = \left[ \begin{matrix} x_1& x_2 & \cdots &x_N \end{matrix} \right]^T \\ Dg = \left[ \begin{matrix} v^T& & \\ & \ddots & \\ & & v^T \end{matrix} \right] v=[x1x2⋯xN]TDg=⎣⎡vT⋱vT⎦⎤
假设一个 v0 是一个 T 为向量,[x1,x2,x3…xN] 记为 v,且都视为列向量。
细心算一下就能发现,下式恰好成立:
v 0 T × [ v T ⋱ v T ] = = 一 维 展 开 ( v 0 × v T ) v_0^T \times \left[ \begin{matrix} v^T& & \\ & \ddots & \\ & & v^T \end{matrix} \right] == 一维展开(v_0 \times v^T) v0T×⎣⎡vT⋱vT⎦⎤==一维展开(v0×vT)
所以Dg可以被替换成a,最后简化成了 BP4 公式。其他几个公式意思差不多。
PS:
[ v k 1 v k 2 ⋯ v k n ] × [ v j 1 T ⋱ v j 1 T ] = [ v k 1 × v j 1 T ⋯ v k n × v j 1 T ] ( 所 有 v 都 是 列 向 量 ) \left[ \begin{matrix} v_{k_1}& v_{k_2} & \cdots &v_{k_n} \end{matrix} \right] \times \left[ \begin{matrix} v_{j_1}^T& & \\ & \ddots & \\ & & v_{j_1}^T \end{matrix} \right] =\left[ \begin{matrix} v_{k_1} \times v_{j_1}^T & \cdots &v_{k_n} \times v_{j_1}^T \end{matrix} \right] (所有 v 都是列向量) [vk1vk2⋯vkn]×⎣⎡vj1T⋱vj1T⎦⎤=[vk1×vj1T⋯vkn×vj1T](所有v都是列向量)
附上用 scala 写的全连接层代码
import breeze.linalg.{DenseMatrix, DenseVector}
import breeze.stats.distributions.Gaussian
/**
* 全连接层
* @param inputSize 输入端维数
* @param outputSize 输出端维数
* @param fn 激活函数
*/
class FullConnectedLayer(inputSize: Int, outputSize: Int, fn: ActivationFunction) {
var weight = DenseMatrix.rand[Double](this.outputSize, this.inputSize, Gaussian(0.0, 1.0))
var bias = DenseVector.rand[Double](this.outputSize, Gaussian(0.0, 1.0))
var inputVec: DenseVector[Double] = null //保留forward的输入
var z:DenseVector[Double] = null //保留forward过程中z的计算结果
/**
* 前向计算
* @param x 输入向量 a[i]
* @return 激活结果 a[i+1]
*/
def forward(x: DenseVector[Double]): DenseVector[Double] = {
this.inputVec = x
this.z = this.bias + (this.weight * this.inputVec)
fn.forward(this.z)
}
/**
* 反向传播
* @param deltaNext delta_a[i+1]
* @return delta_a[i]
*/
def backward(deltaNext: DenseVector[Double]): DenseVector[Double] = {
assert(this.inputVec != null && this.z != null)
val fnDerivate = fn.derivate(this.z)
val deltaZ = deltaNext * fnDerivate
val deltaW = deltaZ * this.inputVec.t
val deltaB = deltaZ
val delta = this.weight.t * deltaZ
this.weight += deltaW
this.bias += deltaB
delta
}
}