强化学习算法DQN：算法简介、创新点：回放机制&target-network、伪代码、算法理解、代码实现、tensorboard展示网络结构

DQN简介

文章利用深度神经网络训练来开发一种新的人工智能体，称为deep Q-network，它可以使用端到端强化学习直接从高维感官输入中学习成功的策略。我们在经典Atari2600游戏的挑战领域测试了这个agent。

证明了deep Q-network agent，仅接收像素和游戏分数作为输入，能够超越所有先前算法的性能，并且在49个游戏中使用相同的算法、网络架构和超参数，达到与专业人类游戏测试者相当的水平。这项工作弥合了高维感官输入和行为之间的鸿沟，产生了第一个能够学习在各种挑战性任务中脱颖而出的人工智能体。

DQN目标

agent的目标是以最大化累积未来回报的方式选择行动。更正式地说，我们使用深度卷积神经网络来逼近最佳作用值函数。

即最大化：在策略$\pi =P(a|s)$下，在状态$s$时采取动作$a$，在第$t$步获得的奖励$r_t$经过$\gamma$折扣之后，得到的累加值。

$$Q^{\ast }(s,a)=\underset{\pi }{\max }\mathbb{E}[r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots |s_t=s,a_t=a,\pi ]$$

Q-learning与DQN

Q-learning是一种用于估计Q函数的离线策略（off-policy）时间差分学习方法（TD）。

在已了解的具有有限个状态以及有限的行为的环境，并对所有可能的$s-a$，进行穷举搜索来寻找最优Q值。若一个环境有许多状态，每个状态下存在多种行为，那么遍历整个环境会浪费大量时间，因此，更好的办法是找到某一参数$\theta$来近似Q函数，即：$$Q(s,a;\theta )\approx Q^{\ast }(s,a)$$

Loss Function

首先，Q-learning的更新规则如下：$$Q(s,a)=Q(s,a)+\alpha (r+\gamma \max Q(s^{{}^{\prime }},a^{{}^{\prime }})-Q(s,a))$$其中，$r+\gamma \max Q(s^{{}^{\prime }},a^{{}^{\prime }})$是目标值，$Q(s,a)$是预测值，目的就是通过学习一种正确的策略使得$Q(s,a)$最小化。

同样的在DQN中，损失函数也定义为目标值与预测值的均方差，同时通过更新权重$\theta$使损失最小化：
$$\begin{array}{rl}loss& =(y_i-Q(s,a;\theta ){)}^2\\ & =(r+\gamma \max Q(s^{{}^{\prime }},a^{{}^{\prime }};{\theta }^{-})-Q(s,a;\theta ){)}^2\end{array}$$ $y_i=r+\gamma \max Q(s^{{}^{\prime }},a^{{}^{\prime }};{\theta }^{-})$为目标值，通过target-network计算出；$Q(s,a;\theta )$为预测值，即为要优化的值，通过value-network算出。

创新点：回放机制&target-network

（与Q-learning相比）

用非线性逼近器，如神经网络，去代表动作Q值时，常常会不稳定甚至不收敛。

这是由于数据之间有较强关联性，不符合神经网络独立同分布的要求。

深度Q网络采取以下两种主要措施来解决此问题：

1. 经验回放方法（reply），对数据进行随机化。消除观测序列中的相关性，并平滑数据中的变化。
2. 使用迭代更新，增加一个新的网络target-network来计算目标值，并周期性更新target-network，从而减少数据的相关性。

注意：强化学习与深层网络体系结构的成功集成，关键取决于采用的重放算法（经验回放reply），该算法解决了最近经历的转换的存储和表示。这与人类大脑的海马体的工作机制有关。

算法伪代码

算法理解

1. 初始化回放记忆$D$，可容纳的数据条数为$N$。
2. 利用随机权值$\theta$（value-network权值），初始化$s-a$ 动作-行为值函数$Q$。
3. 另${\theta }^{-}=\theta$，初始化target-network权值。
4. 循环每次事件episode。
5. 通过初始状态，经预处理之后 得到相应的特征输入。其中$x_i$代表第$i$帧游戏画面。
6. 循环事件中的每一步step。
7. 以$ϵ$大小的概率随机选择一个动作$a_t$；
8. 若上一步中的概率$ϵ$没有发生，则利用贪婪策略选择当前函数值最大的那个动作$a_t=arg{\max }_{a}Q(\varphi (s_t),a;\theta )$。
9. 在仿真器中执行动作$a_t$，获得$r_t$和下一图像$x_{t+1}$。
10. 设置$s_{t+1}=s_t,a_t,x_{t+1}$，预处理${\varphi }_{t+1}=\varphi (s_{t+1})$。
11. 将一个序列$({\varphi }_t,a_t,r_t,{\varphi }_{t+1})$存储在回放记忆$D$中。
12. 从回放记忆$D$中随机采样一个样本数据，记作$({\varphi }_j,a_j,r_j,{\varphi }_{j+1})$。
13. 判断是否一个episode结束，分别使用不同的公式计算$y_j$。
14. 在$loss=(y_i-Q(s,a;\theta ){)}^2$上执行一次梯度下降，获得$\Delta \theta =\alpha (r+\gamma {\max }_{a^{{}^{\prime }}}(s^{{}^{\prime }},a^{{}^{\prime }};{\theta }^{-})-Q(s,a;\theta ))\nabla Q(s,a;\theta )$。
15. 更新网络参数$\theta =\theta +\Delta \theta$。
16. 每隔$C$步更新一次target-network的权值，另${\theta }^{-}=\theta$。
17. 结束每次episode内的循环。
18. 结束所有episode的循环。

代码实现

用深度Q网络构建一个agent，来玩Atari游戏。

首先导入必要的库

import numpy as np
import gym
import tensorflow as tf
from tensorflow.contrib.layers import flatten, conv2d, fully_connected
from collections import deque, Counter
import random
from datetime import datetime

定义一个preprocess_observation函数，对游戏图像进行预处理。减小图像的size，并把图像转换成灰度。

color = np.array([210, 164, 74]).mean()

def preprocess_observation(obs):

    # Crop and resize the image
    img = obs[1:176:2, ::2]

    # Convert the image to greyscale
    img = img.mean(axis=2)

    # Improve image contrast 提高图像对比
    img[img==color] = 0

    # Next we normalize the image from -1 to +1
    img = (img - 128) / 128 - 1

    return img.reshape(88,80,1)

初始化游戏环境

env = gym.make("MsPacman-v0")
n_outputs = env.action_space.n

定义一个q_network函数来构建Q network，输入游戏状态Q network并得到对所有动作的Q值。
网络构成给为三个带有池化的卷积层和一个全连接层。

tf.reset_default_graph()

def q_network(X, name_scope):
    
    # Initialize layers
    initializer = tf.contrib.layers.variance_scaling_initializer()

    with tf.variable_scope(name_scope) as scope: 

        # initialize the convolutional layers
        layer_1 = conv2d(X, num_outputs=32, kernel_size=(8,8), stride=4, padding='SAME', weights_initializer=initializer) 
        tf.summary.histogram('layer_1',layer_1)
        
        layer_2 = conv2d(layer_1, num_outputs=64, kernel_size=(4,4), stride=2, padding='SAME', weights_initializer=initializer)
        tf.summary.histogram('layer_2',layer_2)
        
        layer_3 = conv2d(layer_2, num_outputs=64, kernel_size=(3,3), stride=1, padding='SAME', weights_initializer=initializer)
        tf.summary.histogram('layer_3',layer_3)
        
        # Flatten the result of layer_3 before feeding to the fully connected layer
        flat = flatten(layer_3)

        fc = fully_connected(flat, num_outputs=128, weights_initializer=initializer)
        tf.summary.histogram('fc',fc)
        
        output = fully_connected(fc, num_outputs=n_outputs, activation_fn=None, weights_initializer=initializer)
        tf.summary.histogram('output',output)
        

        # Vars will store the parameters of the network such as weights
        vars = {v.name[len(scope.name):]: v for v in tf.get_collection(key=tf.GraphKeys.TRAINABLE_VARIABLES, scope=scope.name)} 
        return vars, output

定义一个epsilon_greedy函数来执行epsilon-greedy策略，并且是衰减的epsilon-greedy策略。我们希望随着训练的进行，网络会越来越选择更好的Q value对应的action。

epsilon = 0.5
eps_min = 0.05
eps_max = 1.0
eps_decay_steps = 500000

def epsilon_greedy(action, step):
    p = np.random.random(1).squeeze()
    epsilon = max(eps_min, eps_max - (eps_max-eps_min) * step/eps_decay_steps)
    if np.random.rand() < epsilon:
        return np.random.randint(n_outputs)
    else:
        return action

初始化可以存储记忆的经验回放缓冲区的长度为20000。我们可以将(state, action, rewards) 存储到里面，并且从这个里小批量的抽取序列用于训练网络。

buffer_len = 20000
exp_buffer = deque(maxlen=buffer_len)

定义sample_memories函数来从经验回放缓冲区随机抽取序列。

def sample_memories(batch_size):
    perm_batch = np.random.permutation(len(exp_buffer))[:batch_size]
    mem = np.array(exp_buffer)[perm_batch]
    return mem[:,0], mem[:,1], mem[:,2], mem[:,3], mem[:,4]

定义网络超参数

num_episodes = 50
batch_size = 48
input_shape = (None, 88, 80, 1)
learning_rate = 0.001
X_shape = (None, 88, 80, 1)
discount_factor = 0.97

global_step = 0
copy_steps = 100
steps_train = 4
start_steps = 2000

logdir = 'logs'
tf.reset_default_graph()

# Now we define the placeholder for our input i.e game state
X = tf.placeholder(tf.float32, shape=X_shape)

# we define a boolean called in_training_model to toggle the training
in_training_mode = tf.placeholder(tf.bool)

然后搭建主Q网络（primary Q network）和目标Q网络（target Q network）

# we build our Q network, which takes the input X and generates Q values for all the actions in the state
mainQ, mainQ_outputs = q_network(X, 'mainQ')

# similarly we build our target Q network
targetQ, targetQ_outputs = q_network(X, 'targetQ')

# define the placeholder for our action values
X_action = tf.placeholder(tf.int32, shape=(None,))
Q_action = tf.reduce_sum(targetQ_outputs * tf.one_hot(X_action, n_outputs), axis=-1, keep_dims=True)

将primary Q network的参数赋给target Q network

copy_op = [tf.assign(main_name, targetQ[var_name]) for var_name, main_name in mainQ.items()]
copy_target_to_main = tf.group(*copy_op)

使用梯度下降法计算和优化loss function

# define a placeholder for our output i.e action
y = tf.placeholder(tf.float32, shape=(None,1))

# now we calculate the loss which is the difference between actual value and predicted value
loss = tf.reduce_mean(tf.square(y - Q_action))

# we use adam optimizer for minimizing the loss
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

loss_summary = tf.summary.scalar('LOSS', loss)
merge_summary = tf.summary.merge_all()
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())

启动tensorflow会话并运行模型

with tf.Session() as sess:
    init.run()
    
    # for each episode
    for i in range(num_episodes):
        done = False
        obs = env.reset()
        epoch = 0
        episodic_reward = 0
        actions_counter = Counter() 
        episodic_loss = []

        # while the state is not the terminal state
        while not done:

           #env.render()
        
            # get the preprocessed game screen
            obs = preprocess_observation(obs)

            # feed the game screen and get the Q values for each action
            actions = mainQ_outputs.eval(feed_dict={X:[obs], in_training_mode:False})

            # get the action
            action = np.argmax(actions, axis=-1)
            actions_counter[str(action)] += 1 

            # select the action using epsilon greedy policy
            action = epsilon_greedy(action, global_step)
            
            # now perform the action and move to the next state, next_obs, receive reward
            next_obs, reward, done, _ = env.step(action)

            # Store this transistion as an experience in the replay buffer
            exp_buffer.append([obs, action, preprocess_observation(next_obs), reward, done])
            
            # After certain steps, we train our Q network with samples from the experience replay buffer
            if global_step % steps_train == 0 and global_step > start_steps:
                
                # sample experience
                o_obs, o_act, o_next_obs, o_rew, o_done = sample_memories(batch_size)

                # states
                o_obs = [x for x in o_obs]

                # next states
                o_next_obs = [x for x in o_next_obs]

                # next actions
                next_act = mainQ_outputs.eval(feed_dict={X:o_next_obs, in_training_mode:False})


                # reward
                y_batch = o_rew + discount_factor * np.max(next_act, axis=-1) * (1-o_done) 

                # merge all summaries and write to the file
                mrg_summary = merge_summary.eval(feed_dict={X:o_obs, y:np.expand_dims(y_batch, axis=-1), X_action:o_act, in_training_mode:False})
                file_writer.add_summary(mrg_summary, global_step)

                # now we train the network and calculate loss
                train_loss, _ = sess.run([loss, training_op], feed_dict={X:o_obs, y:np.expand_dims(y_batch, axis=-1), X_action:o_act, in_training_mode:True})
                episodic_loss.append(train_loss)
            
            # after some interval we copy our main Q network weights to target Q network
            if (global_step+1) % copy_steps == 0 and global_step > start_steps:
                copy_target_to_main.run()
                
            obs = next_obs
            epoch += 1
            global_step += 1
            episodic_reward += reward
        
        print('Epoch', epoch, 'Reward', episodic_reward,)

结果如下：

Epoch 647 Reward 240.0
Epoch 550 Reward 210.0
Epoch 649 Reward 210.0
Epoch 813 Reward 180.0
Epoch 698 Reward 330.0
Epoch 828 Reward 350.0
Epoch 670 Reward 280.0
Epoch 596 Reward 250.0
Epoch 672 Reward 220.0
Epoch 776 Reward 310.0
Epoch 736 Reward 270.0
Epoch 595 Reward 230.0
Epoch 671 Reward 270.0
Epoch 560 Reward 210.0
Epoch 689 Reward 280.0
Epoch 552 Reward 90.0
Epoch 676 Reward 190.0
Epoch 658 Reward 220.0
Epoch 623 Reward 190.0
Epoch 543 Reward 150.0
Epoch 486 Reward 180.0
Epoch 680 Reward 210.0
Epoch 833 Reward 200.0
Epoch 783 Reward 420.0
Epoch 556 Reward 160.0
Epoch 712 Reward 180.0
Epoch 597 Reward 220.0
Epoch 710 Reward 310.0
Epoch 949 Reward 710.0
Epoch 692 Reward 250.0
Epoch 693 Reward 190.0
Epoch 578 Reward 160.0
Epoch 779 Reward 310.0
Epoch 557 Reward 160.0
Epoch 673 Reward 190.0
Epoch 517 Reward 150.0
Epoch 677 Reward 270.0
Epoch 590 Reward 220.0
Epoch 623 Reward 180.0
Epoch 703 Reward 300.0
Epoch 730 Reward 280.0
Epoch 734 Reward 310.0
Epoch 756 Reward 320.0
Epoch 901 Reward 340.0
Epoch 652 Reward 160.0
Epoch 673 Reward 190.0
Epoch 620 Reward 130.0
Epoch 566 Reward 130.0
Epoch 550 Reward 200.0
Epoch 693 Reward 210.0

tensorboard GRAPHS（网络结构）

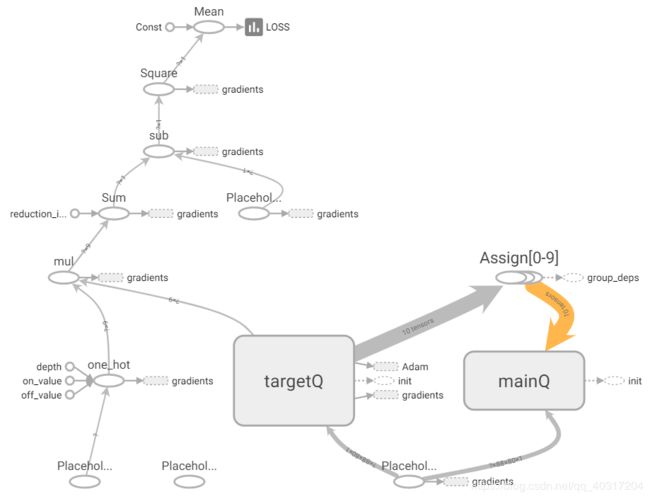
总体网络结构：

（图中targetQ和mainQ的名字位置反了）

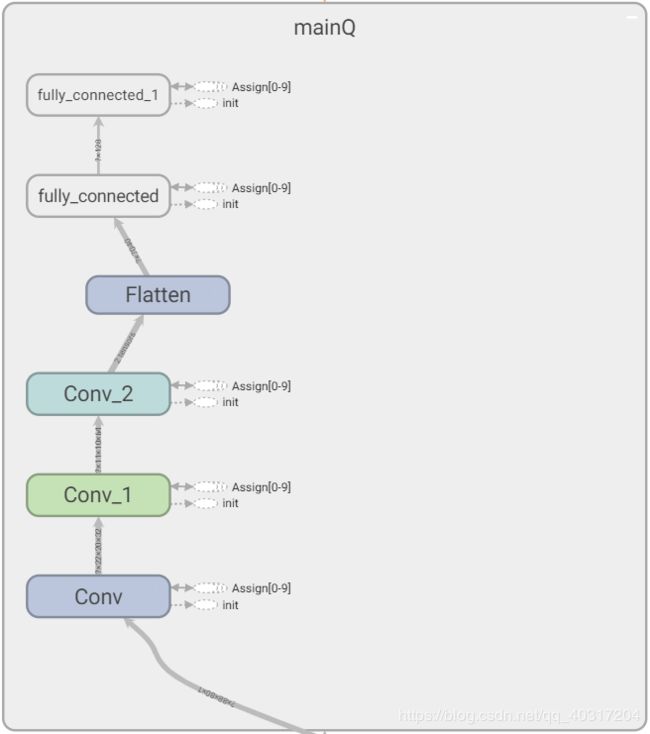
mainQ网络结构：

（图中targetQ命名错误，应该是mainQ）

targetQ网络结构：

（图中mainQ命名错误，应该是targetQ）

总结

1. 对于tensorflow的使用尚不熟悉，需要继续学习。
2. 对于Atari环境的参数不熟悉，需要查看gym的官方文档。