2020杭电多校第五场 Boring Game（模拟）

Problem Description
Given n sheets of paper, place them on the table in pile and fold them in half k times from left to right.

Now from top to bottom, mark a number on paper at each side of the front and back. So there are 2×n×2k numbers in total and these numbers form a permutation P.

Now it expands to its original. These numbers from top to bottom, from front to back, from left to right form a permutation Q.

Given the permutation P, find the permutation Q.

See example for details.

For k=1 and P=1…4×n, you can assume that you are marking the page numbers before printing a booklet forming from n pieces of A4 papers.

Input
The first line contains a single integer T(1≤T≤30) , the number of test cases.

For each test case, the first line gives two integers n, k(1≤n≤200,1≤k≤10).

The next line gives the permutation P that consists of 2×n×2k integers pi(1≤pi≤2×n×2k).

It is guaranteed that ∑2×n×2k doesn’t exceed 106.

Output
The output should contain T lines each containing 2×n×2k integers separated by spaces, indicating the permutation Q.

Sample Input
1
2 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Sample Output
12 5 4 13 11 6 3 14 10 7 2 15 9 8 1 16

题意：

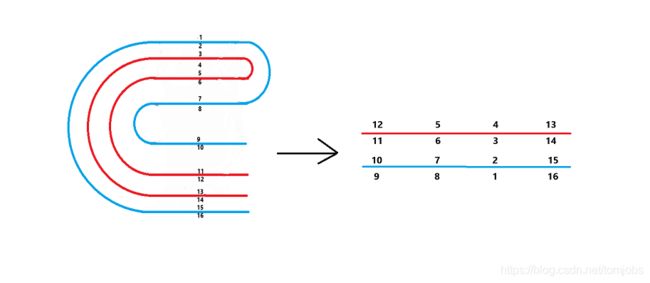
如图，就是n条线，从左向右对折k次，然后按照图中给出的形式还原原来线的数字。

思路：
一直找啥规律，直接模拟还原的过程不就好了吗。。。

#include
#include
#include
#include
#include
#include
#include 
#include 
#include 
#include 
#include 

using namespace std;
typedef long long ll;

const int maxn = 5005 + 7;

deque<pair<int,int>>G[100005];
int P[maxn];

int main() {
    P[0] = 1;
    for(int i = 1;i <= 10;i++) P[i] = P[i - 1] * 2;
    int T;scanf("%d",&T);
    while(T--) {
        int n,k;scanf("%d%d",&n,&k);
        for(int i = n * P[k];i >= 1;i--) {
            int x,y;scanf("%d%d",&x,&y);
            G[i].push_front({x,y});
        }
        int len = n * P[k];
        for(int i = 1;i <= k;i++) {
            for(int j = len;j >= len / 2 + 1;j--) {
                int nex = len - j + 1;
                while(!G[j].empty()) {
                    pair<int,int>now = G[j].front();G[j].pop_front();
                    now = {now.second,now.first};
                    G[nex].push_front(now);
                }
            }
            len /= 2;
        }
        for(int i = n;i >= 1;i--) {
            vector<pair<int,int>>vec;
            while(!G[i].empty()) {
                vec.push_back(G[i].front());G[i].pop_front();
            }
            for(int j = 0;j < vec.size();j++) {
                printf("%d ",vec[j].first);
            }
            for(int j = 0;j < vec.size();j++) {
                printf("%d",vec[j].second);
                if(j == vec.size() - 1 && i == 1) continue;
                else printf(" ");
            }
        }
        printf("\n");
    }
    return 0;
}