《动手学深度学习》学习笔记------3.16. 实战Kaggle比赛:房价预测
《动手学深度学习》学习笔记------3.16. 实战Kaggle比赛:房价预测
预处理
有的特征是 连续数值,例如:MSSubClass;有的特征是离散数值,例如:SaleType。
对上述两类特征分别使用如下方法进行预处理:
(1)连续数值特征的预处理
标准化(standardization):将该特征的每个值先减去均值μ,再除以σ标准差。对于缺失的特征值,替换成该特征的均值。
(2)离散数值特征的预处理
将离散数值转成指示特征。
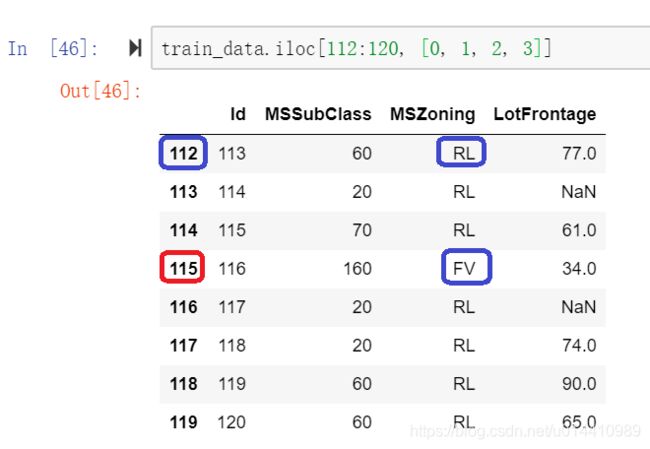
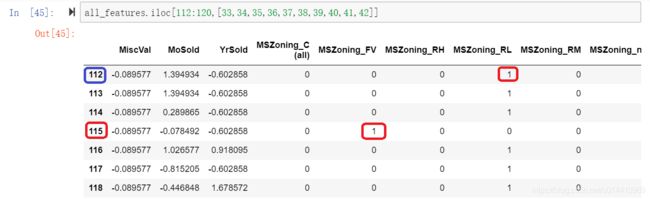
假设特征MSZoning里面有几个不同的离散值FV、RH、RL、RM等,那么这一步转换将去掉MSZoning特征,并新加几个特征MSZoning_FV、MSZoning_RH、MSZoning_RL和MSZoning_RM等,其值为0或1。
如果一个样本原来在MSZoning里的值为RL,那么转换之后MSZoning_RL=1且MSZoning_RM=0。
对于ID = 112的样本,MSZoning属性的取值为 RL,转换之后,MSZoning_RL = 1,并且其他相关属性取值 为0。
对于ID = 115的样本,MSZoning属性的取值为 FV,转换之后,MSZoning_FV = 1,并且其他相关属性取值 为0。
对数均方根误差
另一种常用的评价指标是 均方根误差

两者之间的关系:
对数均方根误差 相当于 先把数据求log,然后再求 均方根误差。
假设我们设计了两种算法,它们的预测结果如下:
| 真值 | 算法1的预测值 | 算法2的预测值 | |
|---|---|---|---|
| 样本1 | 500 | 501 | 508 |
| 样本2 | 2 | 9 | 3 |
如何评价 算法1和算法2哪个更好?
| 评价准则 | 算法1的误差 | 算法2的误差 | 哪个算法好? |
|---|---|---|---|
| 均方根误差 | 5 | 5.7 | 算法1更好 |
| 对数均方根误差 | 1.06 | 0.29 | 算法2更好 |
可以看到,与 均方根误差相比,采用对数均方根误差
(1)当y较大时,可以容忍更大的误差。
(2)当y较小时,期望得到更精确的预测。
课后练习1
问题:
在Kaggle提交本节的预测结果。观察一下,这个结果在Kaggle上能拿到什么样的分数?
解答:
没能成功注册Kaggle帐号,无法尝试。
可以用valid loss估计。
网络:只有一个输出层,没有隐藏层。
训练参数:k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
交叉验证结果:5-fold validation: avg train rmse 0.165232, avg valid rmse 0.170197
在所有训练数据上的 train rmse 0.162533
课后练习2
问题:
对照 ? 折交叉验证结果,不断修改模型(例如添加隐藏层)和调参,能提高Kaggle上的分数吗?
解答:
def get_net():
net = nn.Sequential()
net.add(nn.Dense(218, activation="relu"), nn.Dense(1))
net.initialize()
return net
网络:增加一层隐藏层,该隐藏层的单元个数设置为218。
训练参数:k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
交叉验证结果:5-fold validation: avg train rmse 0.048617, avg valid rmse 0.171843
分析:
(1)训练误差波动很大。需要采用更像的学习率。比如 lr = 0.05.
(2)train loss很小,但是 valid loss很大。说明过拟合。需要增大 weight_dacay。比如增大到100.
重新设置参数。再做一次训练。
网络:增加一层隐藏层,该隐藏层的单元个数设置为218。
训练参数:k, num_epochs, lr, weight_decay, batch_size = 5, 100, 0.05, 100, 64
交叉验证结果:5-fold validation: avg train rmse 0.081824, avg valid rmse 0.130623
在所有训练数据上的train rmse 0.083289
分析:
(1)train loss几乎没有波动。说明减小学习率有效果。
(2)valid loss 仍然大于train loss,说明存在过拟合。继续增大weight_decay后,发现train loss变大,valid loss几乎没有变化。

课后练习3
问题:
如果不使用本节中对连续数值特征的标准化处理,结果会有什么变化?
解答:
不做标准化处理,结果会很差。
课后练习4
问题:
扫码直达讨论区,在社区交流方法和结果。你能发掘出其他更好的技巧吗?
解答:
讨论区网址:
https://discuss.gluon.ai/t/topic/1039
论坛里面大家的方法很多,总结以下,主要有如下几种:
(1)增加一层隐藏层。
(2)隐藏层的激活函数选择 relu,比sigmod性能好。
(3)隐藏层的单元个数设置为几百?我的实验中设置为200和500,在weight decay 为 300时性能相差不是很大。我的实验中设置隐藏层单元个数为 218。
(4)增加隐藏层,相当于提升了网络复杂度。在训练数据只有一千多个的时候,需要通过提高 weight decay来预防过拟合。我的实验中weight decay=100.
(5)网络越复杂,loss函数越不平滑,学习的时候不能使用太大的步长。我的实验中学习率 learning rate设置为0.05.
(6)对房价求log,然后再用L2Loss进行训练。将网络的训练目标和kaggle的评价函数统一起来。(未尝试)
(7)删除某些NA较多的特征。(未尝试)
(8)对某些特征进行log1p,squrt预处理。(未尝试)