算法设计与分析——分治法:详解二维最近点对问题
目录
- 1 前言
- 2 问题描述
- 3 分治法
- 4 暴力求解
- 4.1 算法思路
- 4.2 时间复杂度分析
- 4.3 代码实现
- 5 分治法求解
- 5.1 算法思路
- 5.1.1 数据预处理
- 5.1.2 划分中轴线
- 5.1.3 求半边最小距离
- 5.1.4 求中间的最小距离
- 5.2 代码实现
- 5.2.1 数据预处理
- 5.2.2 分治法
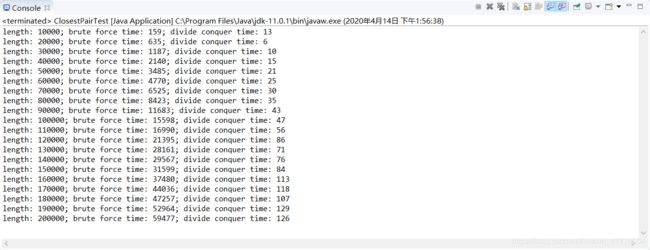
- 6 执行结果
1 前言
本博文是我根据算法实验课的作业整理而成,如若有不严谨和错误的地方,欢迎大家在评论区指出。
转载请注明出处,欢迎大家点赞、收藏,谢谢~
2 问题描述
3 分治法
分治法:将一个规模较大的问题分解为规模较小的子问题,先求解这些子问题,然后将各子问题的解合并得到原问题的解的思路。
递归:直接或间接地调用自身方法。递归通常是解决分治的办法。
- 递归缺点:具体执行步骤理解比较复杂;
- 递归优点:易于实现,大体思路清晰。
4 暴力求解
4.1 算法思路
二维平面上有n个点,则有(n-1)+(n-1)+...+1=n(n-1)/2个点对,依次遍历求出所有点对的距离即可。
4.2 时间复杂度分析
由4.1分析可知,即总共要求出n(n-1)/2个距离,故时间复杂度O(n^2)
4.3 代码实现
public static double getByBruteFoce(double[][] points) {
int head=0;
int tail=points.length-1;
double minDist=getDistance(points,head,head+1);//初始化最小距离
int [] minIndex=new int[] {head,head+1};//初始化最小点对序号
for(int i=head;i<=tail-1;i++) {//遍历求距离
for(int j=i+1;j<=tail;j++) {
if(getDistance(points,i,j)<minDist) {
minDist=getDistance(points,i,j);//更新点对最小距离
minIndex[0]=i;//更新点对序号
minIndex[1]=j;
}
}
}
return minDist;
}
5 分治法求解
5.1 算法思路
核心思想:
- 数据预处理
- 划分中轴线
- 求出左边的最小距离
- 求出右半边的最小距离
- 求出中间的最小距离
- 比较这三个最小距离
5.1.1 数据预处理
因为这些点的位置是随机产生并保存在二维数组中,所以我们得先将这些点,按照x坐标从小到大排序,调整它们在二维数组中的次序。比如:最左边的点,它的位置就保存在二维数组的第一个元素中;
5.1.2 划分中轴线
把这些点在平面上分成左右两边。
依据什么来划分中轴线?
选择最中间的两个元素,求出它俩x坐标的平均值,设置为中轴线的坐标。
5.1.3 求半边最小距离
左半边和右半边的求最小距离的方法是一样的。
假如我们现在求的是左半边,那就把左半边也看成一个整体,我们再把它分成左右两半,依次往下递归,越分越小。
递归何时中止?
分到点只剩很小的时候就终止,比如本文在后面附加的代码中,是当平面只剩下4个点时就不再切分。
5.1.4 求中间的最小距离
中间区域应该划分多宽?
我们只需要考查中轴线左右两边距离小于d的点。
理由:距离中轴线大于d的那些点,它们和另一个半边的点的距离,肯定大于d,考查他们就没有意义了。
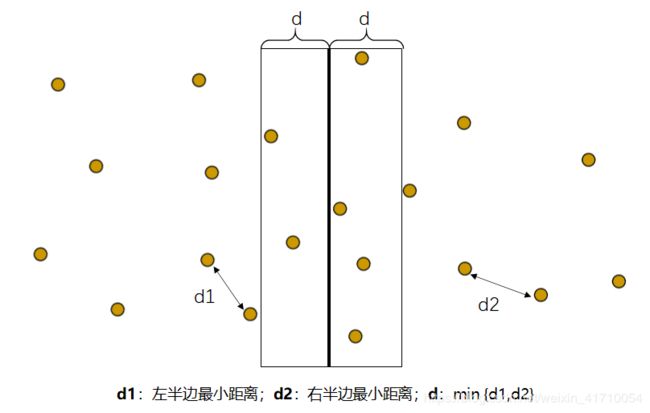
那么,现在我们只需要对上图的左侧2个点和右侧4个点分别进行比较即可。
如何进一步优化?
比如我们现在选取了左侧的m点,但实际上,我们不必跟右侧的4个点都比较,只需跟右侧的阴影部分(d*2d)以内的点进行比较,也就是,跟m点垂直距离在d以内的那两个点。
原因:如果两点之间垂直距离大于d,那么这两点间距必然大于d,考查他们也没有意义。
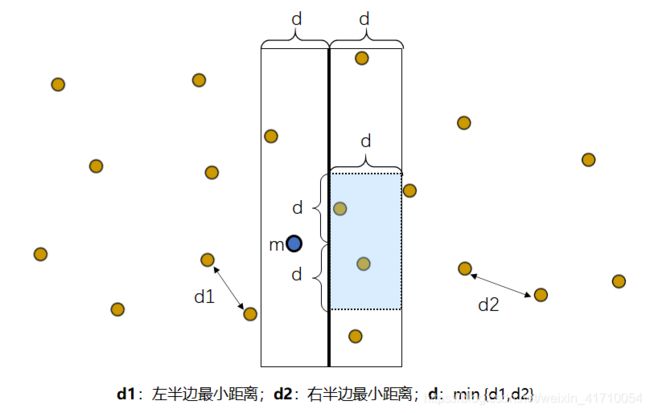
关于矩形的进一步说明
如果查阅过其他资料,或许你听过,我们划分出的d*2d区域中,最多只能有6个点。
因为我们已知两侧的最小距离为d,而d*2d的区域中的点是同一侧的。因此这些点的距离必然大于等于d,经过数学几何知识,我们可以算出这个区域最多只能有6个点。
5.2 代码实现
5.2.1 数据预处理
在这里,我是采用了效率较高的快速排序算法。
//数据预处理:将点按照横坐标由小到大排序
//快速排序
private static double[][] quickSort(double[][] oldData) {
double[][] newData=oldData.clone();
QSRecursion(newData,0,newData.length-1);
return newData;
}
private static void QSRecursion(double[][] newData, int i, int j) {
if(i==j)return;
int standardIndex=i+new java.util.Random().nextInt(j-i+1);
int pivot=partition(newData,i,j,standardIndex);//保存基准元素的正确位置
if(pivot!=i)QSRecursion(newData,i,pivot-1);//左边
if(pivot!=j)QSRecursion(newData,pivot+1,j);//右边
}
private static int partition(double[][] newData, int i, int j, int standardIndex) {
swap(newData,i,standardIndex);//将序列首个元素和基准元素对换位置
int left=i+1;//i为头指针
int right=j;//j为尾指针
while(left<right) {
while(newData[left][0]<=newData[i][0]&left<right) {
left++;
}
while(newData[right][0]>=newData[i][0]&left<right) {
right--;
}
if(left<right) {
swap(newData,right,left);//对换位置,保证左小右大
}
}
if(newData[right][0]>newData[i][0]) {
swap(newData,right-1,i);
standardIndex=right-1;
}else {
swap(newData,j,i);
standardIndex=j;
}
return standardIndex;
}
private static void swap(double[][] newData, int a, int b) {//对换位置
double[] temp=newData[a];
newData[a]=newData[b];
newData[b]=temp;
}
5.2.2 分治法
//分治法求解
public static double getByDivideConquer(double[][] points) {
if(points.length==1|points.length==0) {
return 0;
}
double[][] pointsSorted=quickSort(points);
// for(int i=0;i
// {
// System.out.println(pointsSorted[i][0]);
//
// }
int head=0;
int tail=pointsSorted.length-1;
int [] minIndex=getByDivideConquer(pointsSorted,head,tail);
double minDist=getDistance(pointsSorted,minIndex[0],minIndex[1]);
return minDist;
}
/////////////////////////////////////////////
private static int[] getByDivideConquer(double[][] points, int head, int tail) {
double minDist=getDistance(points,head,head+1);//初始化最小距离
int [] minIndex=new int[] {head,head+1};//初始化最小点对序号
if(tail-head+1<=4) {//点数小于等于4时
for(int i=head;i<=tail-1;i++) {//遍历求距离
for(int j=i+1;j<=tail;j++) {
if(getDistance(points,i,j)<minDist) {
minDist=getDistance(points,i,j);
minIndex[0]=i;
minIndex[1]=j;
}
}
}
}else {
int [] minIndexLeft=getByDivideConquer(points,head,head+(tail-head)/2);
int [] minIndexRight=getByDivideConquer(points,head+(tail-head)/2+1,tail);
double minDisLeft=getDistance(points,minIndexLeft[0],minIndexLeft[1]);
double minDisRight=getDistance(points,minIndexRight[0],minIndexRight[1]);
double minDisTwoSide=Math.min(minDisLeft, minDisRight);//即d
if(minDisLeft>=minDisRight) {
minDist=minDisRight;
minIndex=minIndexRight;
}else {
minDist=minDisLeft;
minIndex=minIndexLeft;
}
double middleAxis=(points[head+(tail-head)/2][0]+points[head+(tail-head)/2+1][0])/2;//设置中间线,该变量为中间线的x轴坐标
int i=head+(tail-head)/2+1;//中间线右边的点
while(i<=tail&&(points[i][0]-middleAxis<minDisTwoSide)) {//i点没越界且和中间线的x轴距离小于d
{
int count=0;
for(int j=head+(tail-head)/2;j>=head&&(points[j][0]-middleAxis<minDisTwoSide)&&(count<=6);j--) {//j点没越界且符合条件的个数小于6
if(Math.abs(points[j][1]-points[j][1])<minDisTwoSide) {//找出d*2d矩形的点
if(getDistance(points,i,j)<minDist) {
minDist=getDistance(points,i,j);
minIndex[0]=i;
minIndex[1]=j;
}
count++;
}
}
i++;
}
}
}
return minIndex ;
}
//////////////////////////////////////////////////
//计算点i和点j的距离
private static double getDistance(double[][] points, int i, int j) {
double dis=Math.sqrt(Math.pow(points[i][0]-points[j][0], 2)+Math.pow(points[i][1]-points[j][1], 2));
//System.out.println(dis);//测试输出
return dis;
}