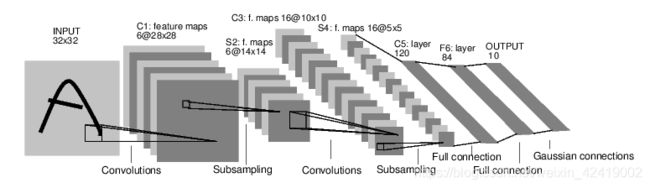
3 PyTorch 官网教材之 搭建一个最简单的神经网络 LeNet NEURAL NETWORKS

---

官网教材 搭建一个最简单的神经网络

时间：2019年6月21日16:59:08

官网链接：

https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html

1. 结构顺序通常是 卷积>激活>池化，或全连接>激活。BN好像在卷积或者激活之后都是可以的，影响不大。

2. 卷积、全连接有参数，需要现在__init__()中定义，再在forward() 中使用。

3. python 中函数可以先使用后定义。

4. self.fc1 = nn.Linear(16 * 6 * 6, 120) 第一个全连接输入中 6 是如何计算出来的。

• 6 * 6 from image dimension 将前面卷积产生的所有数据（16 * 6 * 6 中的16 是16个通道，6 * 6 是每个图片的尺寸（这个尺寸是图片多次卷积池化之后的尺寸，是需要通过一步一步的计算的）））。view 之后输入全连接层，所以全连接的输入大小应须和最后一个卷积之后的所有通道的点的数目之和相同。 120 是人为设定的，可以更改。

5. LeNet-5，的卷积层和全连接一共有5层，权重就应该有10层，因为每一层之后有偏置。

ReLU激活层 和 池化层 是没有参数的。

后续还要学习的BN不需要设置偏置。

1. 定义网路结构

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)  #  输入一张图片，产生6个通道（图片），是通过3 * 3的卷积得到的6个通道。6 和 3 都是人为设定的参数，可以改变。（参数3,指的是filter的大小是（3*3））
        self.conv2 = nn.Conv2d(6, 16, 3)  # 第二词卷积核输入大小须和第一次卷积大小的输出相同。16 和 3 是人为设定的，可更改。
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension  将前面卷积产生的所有数据（16 * 6 * 6 中的16 是16个通道，6 * 6 是每个图片的尺寸（这个尺寸是图片多次卷积池化之后的尺寸，是需要通过一步一步的计算的）））。view 之后输入全连接层，所以全连接的输入大小应须和最后一个卷积之后的所有通道的点的数目之和相同。 120 是人为设定的，可以更改。
        self.fc2 = nn.Linear(120, 84)  #  120 是由前一个全连接的输出决定的，84是人为设定的，可以更改。
        self.fc3 = nn.Linear(84, 10)  # 84 是由前一个全连接的输出决定的，10是人为设定的，可以更改。因为这个网络最终的目的是进行一个10分类的图像分类任务所以，最后作者定义全连接层的输出是10个点。

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))  #  卷积、激活、池化，一行写。
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)  # 这里池化的 2 和（2, 2）等价, 4合1，改变图片的分辨率，缩小图片。
        x = x.view(-1, self.num_flat_features(x))  # 将所有通道的图片view 成一个一维的数据，用于后续的全连接层输入。
        x = F.relu(self.fc1(x))  # 全连接、激活，一行代码。
        x = F.relu(self.fc2(x))
        x = self.fc3(x)  # 最后一层，只全连接，不激活。
        return x # 输出 10 个数据（点）

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

2. 显示网络结构：

Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=576, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

• 10类分类网络 LeNet-5 的经典结构（与上面的程序不完全相同），输入是单通道的（32*32）图片(即和灰度图)：
  

3. 显示网路权重

params = list(net.parameters())  # 所有的网络参数
print(len(params))
print(params[0].size()) # conv1's .weight
print(params[1].size()) 
print(params[2].size()) 
print(params[3].size())  
print(params[4].size())  
print(params[5].size())  
print(params[6].size()) 
print(params[7].size()) 
print(params[8].size())  
print(params[9].size())  

对应的输出结果如下（网络结构的参数输出大小如下）：

• 注意：定义网络结构的时候输入特征个数写在输出特征的前面nn.Conv2d(1, 6, 3)，但输出网络结构权重的时候，输入特征个数在输入特征的后面torch.Size([6, 1, 3, 3])。

10
torch.Size([6, 1, 3, 3])  # 1个通道（图片）经过相同权重的3*3卷积得到6个不同的通道。
torch.Size([6])   # 产生6个通道中1个通道需要1个偏置，和1个filter, 每个filter的大小是3*3。
torch.Size([16, 6, 3, 3])  # 同时使用6个通道，经过相同权重的3*3filter得到16个不同的通道。
torch.Size([16])  # 产生16个通道中1个通道需要1个偏置，和6个filter, 每个filter的大小是3*3。
torch.Size([120, 576])  #  经过卷积、池化、卷积、池化之后图片从输入时的单通道（32， 32）变成了现在的（6， 6），所以张量的大小是 16 * 6 * 6 = 576。全连接层之间的参数个数等于 全连接的输入神经元的个数 *  输出神经元的个数 + 输出神经元的个数（偏置）。
torch.Size([120])  # 输出 120个点，就有120个偏置。
torch.Size([84, 120])
torch.Size([84])
torch.Size([10, 84])
torch.Size([10])

4. 网络的输出和反向传播

input = torch.randn(1, 1, 32, 32)  #  使用随机数来模拟一张（32* 32）的输入图片。
out = net(input)  #  相当于net.forward(input) 正向计算
print(out)

net.zero_grad()  #  Zero the gradient buffers of all parameters 将缓存中的权重参数w的梯度重置为零 
out.backward(torch.randn(1, 10))  # and backprops with random gradients 反向传播并对权重w进行求偏导，将x(输入数据)的值带入偏导方程，再结合学习率，更新一次权重w的值。

网络的输出结果如下（10分类结果）：

tensor([[-0.0330, -0.1659, -0.0343, -0.1814,  0.1950, -0.0039,  0.1094, -0.0088,
         -0.0468, -0.0164]], grad_fn=<AddmmBackward>)

5. Loss Function 计算

Loss 的作用：estimates how far away the output is from the target.

1. 计算定义

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)  # tensor(1.4625, grad_fn=)

2. 计算过程

• loss.grad_fn 显示梯度计算方式

• LeNet 网络的 Loss 计算过程：

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d -> view -> linear -> relu -> linear -> relu -> linear -> MSELoss -> loss

• 将最后的三个的计算方式 如下：

print(loss.grad_fn)  # MSELoss 最后一步loss的计算过程，同时应该理解为反向传播时的第一步。
print(loss.grad_fn.next_functions[0][0])  # Linear 使用next_ 的原因是因为反向来了。
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

#   # MSELoss
#   # Linear 
#   # ReLU

3. 梯度更新前后额对比： gradient

• gradient buffers 梯度缓冲区（存储的是梯度，简单理解是斜率，是变化率，而不是当前的数值。）
• 这里只显示了 网络中第一层卷积的偏置的梯度（6个数）更新

net.zero_grad()     # zeroes the gradient buffers of all parameters
print(net.conv1.bias.grad) # tensor([0., 0., 0., 0., 0., 0.])

loss.backward()
print(net.conv1.bias.grad)  # tensor([-0.0060,  0.0266,  0.0337, -0.0046,  0.0068,  0.0114])

4. 显示更新后的 gradient 梯度值（斜率值、权重的变化速度）

print(net.conv1)  #  第一个卷积层的所有数据
print(net.conv1.bias)  # 偏置的信息
print(net.conv1.bias.grad)  # 偏置的数据值

网络参数输出如下：

Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))

Parameter containing:
tensor([-0.1618, -0.1601, -0.0773, -0.1067, -0.1815,  0.1880],
       requires_grad=True)
       
tensor([-0.0372, -0.0342,  0.0513, -0.0003,  0.0370,  0.0150])

5. 更新 weight 权重 的三个步骤（使用之前计算的 gradient 梯度值来更新权重）: weight = weight - learning_rate * gradient

• update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # 一步， gradient 梯度重置为0。zero the gradient buffers  

output = net(input)
loss = criterion(output, target)

loss.backward()  #  第二步， 根据 loss 反向计算 gradient 梯度
optimizer.step()    # 第三步， 更新 weight 权重。Does the update  

• 反向传播 loss.backward() 是最耗时的。

THE END