全连接层详解

注：本系列博客在于汇总CSDN的精华帖，类似自用笔记，不做学习交流，方便以后的复习回顾，博文中的引用都注明出处，并点赞收藏原博主

1、什么是全连接层：

全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”（下面会讲到这个分布式特征）映射到样本标记空间的作用。在实际使用中，全连接层可由卷积操作实现：

对前层是全连接的全连接层可以转化为卷积核为1x1的卷积；而前层是卷积层的全连接层可以转化为卷积核为hw的全局卷积，hw分别为前层卷积结果的高和宽。

全连接的核心操作就是矩阵向量乘积 y = Wx

转载于：https://blog.csdn.net/qq_39521554/article/details/81385159

2、怎么理解全连接层：

---

假设你是一只小蚂蚁，你的任务是找小面包。你的视野还比较窄，只能看到很小一片区域。当你找到一片小面包之后，你不知道你找到的是不是全部的小面包，所以你们全部的蚂蚁开了个会，把所有的小面包都拿出来分享了。全连接层就是这个蚂蚁大会~

3、进一步理解⭐⭐⭐

以下内容转载于：https://blog.csdn.net/m0_37407756/article/details/80904580

例如经过卷积，relu后得到3x3x5的输出。

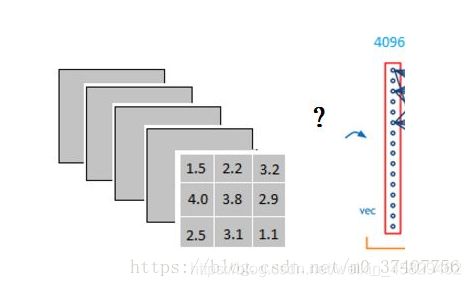
那它是怎么样把3x3x5的输出，转换成1x4096的形式？

很简单,可以理解为在中间做了一个卷积。

从上图我们可以看出，我们用一个3x3x5的filter 去卷积激活函数的输出，得到的结果就是一个fully connected layer 的一个神经元的输出，这个输出就是一个值。因为我们有4096个神经元。我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出。

举个简单的例子：

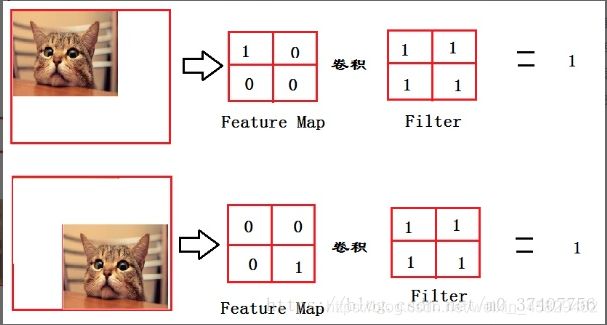
从上图我们可以看出，猫在不同的位置，输出的feature值相同，但是位置不同。

对于电脑来说，特征值相同，但是特征值位置不同，那分类结果也可能不一样。

这时全连接层filter的作用就相当于

喵在哪我不管，我只要喵，于是我让filter去把这个喵找到，

实际就是把feature map 整合成一个值，这个值大，有喵，这个值小，那就可能没喵

和这个喵在哪关系不大了，鲁棒性有大大增强。

因为空间结构特性被忽略了，所以全连接层不适合用于在方位上找Pattern的任务，比如segmentation。

全连接层中一层的一个神经元就可以看成一个多项式（类似加权平均），我们用许多神经元去拟合数据分布

但是！！！只用一层fully connected layer 有时候没法解决非线性问题，

而如果有两层或以上fully connected layer就可以很好地解决非线性问题了

---

4、全连接层的作用：

---

通过特征提取，实现分类

我们现在的任务是去区别一图片是不是猫

假设这个神经网络模型已经训练完了，全连接层已经知道

当我们得到以上特征，我就可以判断这个东东是猫了。

因为全连接层的作用主要就是实现分类（Classification）

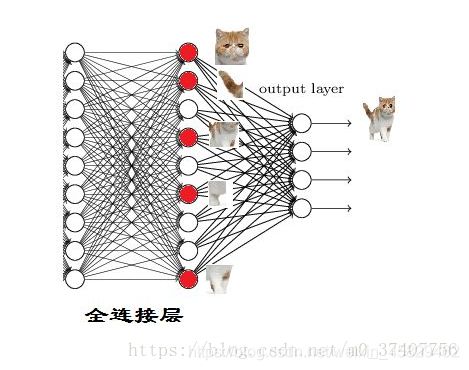
红色的神经元表示这个特征被找到了（激活了）

同一层的其他神经元，要么猫的特征不明显，要么没找到

当我们把这些找到的特征组合在一起，发现最符合要求的是猫

ok，我认为这是猫了

这细节特征又是怎么来的？

就是从前面的卷积层，下采样层来的

5、全连接层的注意层面：

---

全连接层参数特多（可占整个网络参数80%左右）

那么全连接层对模型影响参数就是三个：

1，全接解层的总层数（长度）
2，单个全连接层的神经元数（宽度）
3，激活函数

首先我们要明白激活函数的作用是：增加模型的非线性表达能力

6、torch代码小结

---

以下设置了三个全连接层，大家留意每一层的filter

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        #nn.Module子类的函数必须在构建函数中执行父类的构造函数
        #下式等价于nn.Module.__init__(self)
        super(Net, self).__init__()
        #卷积层“1”表示输入图片为单通道，“6”表示输出通道数,‘5’表示卷积核为5*5
        self.conv1 = nn.Conv2d(1, 6, 5)
        #卷积层
        self.conv2 = nn.Conv2d(6, 16, 5)
        #全连接层，y=Wx+b
        self.fc1 = nn.Linear(16*5*5, 120)
        #参考第三节，这里第一层的核大小是前一层卷积层的输出和核大小16*5*5，一共120层
        self.fc2 = nn.Linear(120, 84)
        #接下来每一层的核大小为1*1
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        #卷积--激活--池化
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        #reshape ,'-1'表示自适应
        x = x.view(x.size()[0], -1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3
        return x

net = Net()
print(net)

self.fc1 = nn.Linear(1655, 120)
#参考第三节，这里第一层的核大小是前一层卷积层的输出和核大小1655，一共120层
self.fc2 = nn.Linear(120, 84)
#接下来每一层的核大小为1*1
self.fc3 = nn.Linear(84, 10)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)