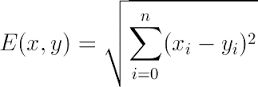一、KNN算法概述
邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。Cover和Hart在1968年提出了最初的邻近算法。KNN是一种分类(classification)算法,它输入基于实例的学习(instance-based learning),属于懒惰学习(lazy learning)即KNN没有显式的学习过程,也就是说没有训练阶段,数据集事先已有了分类和特征值,待收到新样本后直接进行处理。与急切学习(eager learning)相对应。
KNN是通过测量不同特征值之间的距离进行分类。
思路是:如果一个样本在特征空间中的k个最邻近的样本中的大多数属于某一个类别,则该样本也划分为这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
提到KNN,网上最常见的就是下面这个图,可以帮助大家理解。
我们要确定绿点属于哪个颜色(红色或者蓝色),要做的就是选出距离目标点距离最近的k个点,看这k个点的大多数颜色是什么颜色。当k取3的时候,我们可以看出距离最近的三个,分别是红色、红色、蓝色,因此得到目标点为红色。
算法的描述:
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类
二、关于K的取值
K:临近数,即在预测目标点时取几个临近的点来预测。
K值得选取非常重要,因为:
如果当K的取值过小时,一旦有噪声得成分存在们将会对预测产生比较大影响,例如取K值为1时,一旦最近的一个点是噪声,那么就会出现偏差,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
如果K的值取的过大时,就相当于用较大邻域中的训练实例进行预测,学习的近似误差会增大。这时与输入目标点较远实例也会对预测起作用,使预测发生错误。K值的增大就意味着整体的模型变得简单;
如果K==N的时候,那么就是取全部的实例,即为取实例中某分类下最多的点,就对预测没有什么实际的意义了;
K的取值尽量要取奇数,以保证在计算结果最后会产生一个较多的类别,如果取偶数可能会产生相等的情况,不利于预测。
K的取法:
常用的方法是从k=1开始,使用检验集估计分类器的误差率。重复该过程,每次K增值1,允许增加一个近邻。选取产生最小误差率的K。
一般k的取值不超过20,上限是n的开方,随着数据集的增大,K的值也要增大。
三、关于距离的选取
距离就是平面上两个点的直线距离
关于距离的度量方法,常用的有:欧几里得距离、余弦值(cos), 相关度 (correlation), 曼哈顿距离 (Manhattan distance)或其他。
Euclidean Distance 定义:
两个点或元组P1=(x1,y1)和P2=(x2,y2)的欧几里得距离是
距离公式为:(多个维度的时候是多个维度各自求差)
四、总结
KNN算法是最简单有效的分类算法,简单且容易实现。当训练数据集很大时,需要大量的存储空间,而且需要计算待测样本和训练数据集中所有样本的距离,所以非常耗时
KNN对于随机分布的数据集分类效果较差,对于类内间距小,类间间距大的数据集分类效果好,而且对于边界不规则的数据效果好于线性分类器。
KNN对于样本不均衡的数据效果不好,需要进行改进。改进的方法时对k个近邻数据赋予权重,比如距离测试样本越近,权重越大。
KNN很耗时,时间复杂度为O(n),一般适用于样本数较少的数据集,当数据量大时,可以将数据以树的形式呈现,能提高速度,常用的有kd-tree和ball-tree。
(弱小无助。。。根据许多大佬的总结整理的)
五、Python实现
根据算法的步骤,进行kNN的实现,完整代码如下
1 import numpy as np 2 from math import sqrt 3 import operator as opt 4 5 def normData(dataSet): 6 maxVals = dataSet.max(axis=0) 7 minVals = dataSet.min(axis=0) 8 ranges = maxVals - minVals 9 retData = (dataSet - minVals) / ranges 10 return retData, ranges, minVals 11 12 13 def kNN(dataSet, labels, testData, k): 14 distSquareMat = (dataSet - testData) ** 2 # 计算差值的平方 15 distSquareSums = distSquareMat.sum(axis=1) # 求每一行的差值平方和 16 distances = distSquareSums ** 0.5 # 开根号,得出每个样本到测试点的距离 17 sortedIndices = distances.argsort() # 排序,得到排序后的下标 18 indices = sortedIndices[:k] # 取最小的k个 19 labelCount = {} # 存储每个label的出现次数 20 for i in indices: 21 label = labels[i] 22 labelCount[label] = labelCount.get(label, 0) + 1 # 次数加一 23 sortedCount = sorted(labelCount.items(), key=opt.itemgetter(1), reverse=True) # 对label出现的次数从大到小进行排序 24 return sortedCount[0][0] # 返回出现次数最大的label 25 26 27 28 if __name__ == "__main__": 29 dataSet = np.array([[2, 3], [6, 8]]) 30 normDataSet, ranges, minVals = normData(dataSet) 31 labels = ['a', 'b'] 32 testData = np.array([3.9, 5.5]) 33 normTestData = (testData - minVals) / ranges 34 result = kNN(normDataSet, labels, normTestData, 1) 35 print(result)
六、sklearn库的应用
我利用了sklearn库来进行了kNN的应用(这个库是真的很方便了,可以借助这个库好好学习一下,我是用KNN算法进行了根据成绩来预测,这里用一个花瓣萼片的实例,因为这篇主要是关于KNN的知识,所以不对sklearn的过多的分析,而且我用的还不深入?)
sklearn库内的算法与自己手搓的相比功能更强大、拓展性更优异、易用性也更强。还是很受欢迎的。(确实好用,简单)
1 from sklearn import neighbors //包含有kNN算法的模块 2 from sklearn import datasets //一些数据集的模块
调用KNN的分类器
1 knn = neighbors.KNeighborsClassifier()
预测花瓣代码
from sklearn import neighbors from sklearn import datasets knn = neighbors.KNeighborsClassifier() iris = datasets.load_iris() # f = open("iris.data.csv", 'wb') #可以保存数据 # f.write(str(iris)) # f.close() print iris knn.fit(iris.data, iris.target) #用KNN的分类器进行建模,这里利用的默认的参数,大家可以自行查阅文档 predictedLabel = knn.predict([[0.1, 0.2, 0.3, 0.4]]) print ("predictedLabel is :" + predictedLabel)
上面的例子是只预测了一个,也可以进行数据集的拆分,将数据集划分为训练集和测试集
from sklearn.mode_selection import train_test_split #引入数据集拆分的模块 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
关于 train_test_split 函数参数的说明:
train_data:被划分的样本特征集
train_target:被划分的样本标签
test_size:float-获得多大比重的测试样本 (默认:0.25)
int - 获得多少个测试样本
random_state:是随机数的种子。
写在后面
因为最近在做一个比赛的项目,关于大数据分析与挖掘的,所以写一些相关的博客来记录一下,包括关于python数据分析与挖掘的知识、pyqt的一些知识和机器学习的相关知识以及在做项目中遇到的一些问题。
还是在校大学生,知识面不全,也参考了网上许多大佬的博客,一些个人的理解与应用可能有问题,欢迎大家指正,有学到新的相关知识也会对文章进行更新。
有想交流的,欢迎Q我(看博客侧边栏~)