CF 505 D. Recovering BST 区间DP

D. Recovering BST

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dima the hamster enjoys nibbling different things: cages, sticks, bad problemsetters and even trees!

Recently he found a binary search tree and instinctively nibbled all of its edges, hence messing up the vertices. Dima knows that if Andrew, who has been thoroughly assembling the tree for a long time, comes home and sees his creation demolished, he'll get extremely upset.

To not let that happen, Dima has to recover the binary search tree. Luckily, he noticed that any two vertices connected by a direct edge had their greatest common divisor value exceed 11.

Help Dima construct such a binary search tree or determine that it's impossible. The definition and properties of a binary search tree can be found here.

Input

The first line contains the number of vertices nn (2≤n≤7002≤n≤700).

The second line features nn distinct integers aiai (2≤ai≤1092≤ai≤109) — the values of vertices in ascending order.

Output

If it is possible to reassemble the binary search tree, such that the greatest common divisor of any two vertices connected by the edge is greater than 11, print "Yes" (quotes for clarity).

Otherwise, print "No" (quotes for clarity).

Examples

Input

Copy

6
3 6 9 18 36 108

Output

Copy

Yes

Input

Copy

2
7 17

Output

Copy

No

Input

Copy

9
4 8 10 12 15 18 33 44 81

Output

Copy

Yes

Note

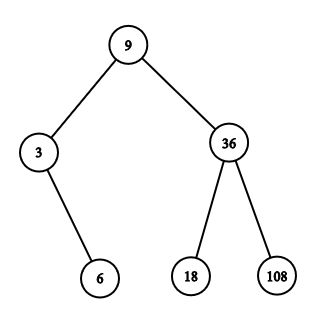
The picture below illustrates one of the possible trees for the first example.

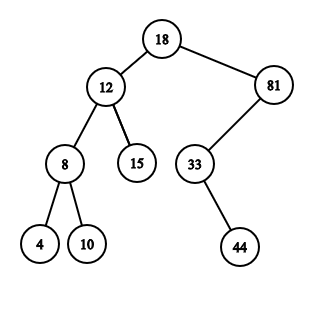
The picture below illustrates one of the possible trees for the third example.

 

解题思路：区间DP

g[i][j]表示num[i]和num[j]是否可以联边

left[i][j]表示从i到j随意变形能否成为j+1的左子树

right[i][j]表示从i到j随意变形能否成为i-1的右子树

 

AC代码

#include 
#include
using namespace std;


/*
long long num[703];
int sign=0;

bool b_search(long long l,long long r,long long father)
{
    if(l==r)
    {
        if(__gcd(num[l],father)!=1)
            return true;
        else
            return false;
    }
    else
    {
        int m;
        for(m=l;m<=r;++m)
        {
            if(father==-1||__gcd(num[m],father)!=1)
            {
                bool temp1=true;
                bool temp2=true;
                if(l<=m-1)
                    temp1=b_search(l,m-1,num[m]);
                if(r>=m+1)
                    temp2=b_search(m+1,r,num[m]);
                if(temp1==true&&temp2==true)
                    return true;
                else
                    continue;
            }
        }
        return false;

    }
}

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;++i)
        cin>>num[i];
    if(b_search(1,n,-1))
        cout<<"Yes"<>n;
    for(int i=1;i<=n;++i)
        cin>>num[i];
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            g[i][j]=(__gcd(num[i],num[j])!=1);
    for(int len=0;len<=n-1;++len)
    {
        for(int l=1;l<=n-len;++l)
        {
            int r=l+len;
            for(int mid=l;mid<=r;++mid)
            {
                if((lmid?Right[mid+1][r]:1))
                {
                    if(g[mid][l-1]) Right[l][r]=1;
                    if(g[mid][r+1]) Left[l][r]=1;
                }
            }
        }
    }
    for(int mid=1;mid<=n;++mid)
    {
        if((mid>1?Left[1][mid-1]:1)&&(mid