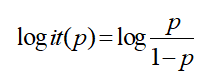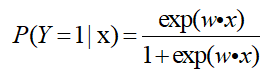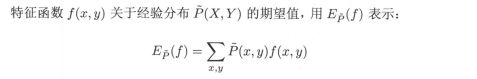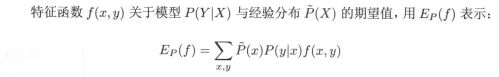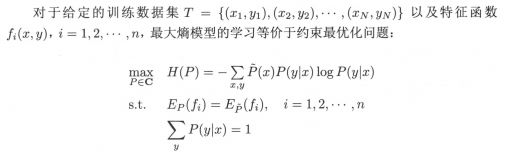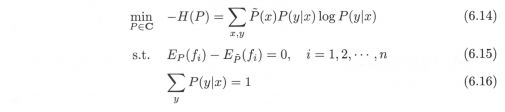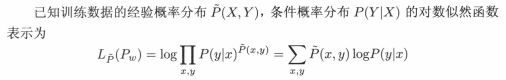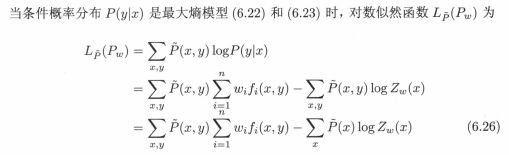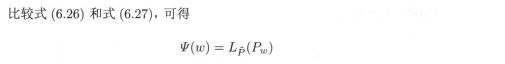今天是2020年2月12日星期三,现在对学习有点麻木。看了一天的最大熵模型,多少理解了一些内容,在学校看的啥啊真是,要不是写这个博客,关键的地方真是一点看不出来啊。反思再反思,看书的时候难懂的地方直接翻过去了,现在为了写出来,多查了很多资料。切忌眼高手低啊,不把模型真正用出来,很难有深入的理解啊。
本章标题为逻辑斯谛回归与最大熵模型,这是两个部分,不能混为一谈。当然了放在一起肯定有李航老师的道理,最后会分析两者联系。最大熵模型还是比较难懂的,这里仅是记录我的学习过程,欢迎讨论,仅作参考,谢绝采纳。
GitHub:https://github.com/wangzycloud/statistical-learning-method
逻辑斯谛回归模型
引入
首先要说下,“逻辑斯谛”这个名字真是蛮奇怪的,可能因为我还是比较没文化吧。脑子里先入为主,总是想把吴恩达老师CS229上逻辑回归算法的名字安放到这个模型上。所以接下来,都会以“逻辑回归”这个名字代替书中的“逻辑斯谛回归”。不得不说,该算法从一个特殊的函数出发,发现了可将输入变量x的线性函数值转变为分类类别的概率。
逻辑斯谛分布
首先来看一下这个逻辑斯谛分布和概率密度函数:
分布函数属于逻辑斯谛函数,图形像一条S型曲线,在中心附近增长较快,在两端增长速度较慢。形状参数γ的值越小,中心附近增长越快。
二项逻辑回归模型
作为分类模型,顾名思义,二项逻辑回归模型是一种二分类算法,由条件概率分布P(Y|X)表示,随机变量X取实数,随机变量Y取值为0或1。
这里得出类别结果的过程与朴素贝叶斯算法类似(这里强调的是,需要得到P(Y=1)和P(Y=0),两算法本身差别很大),每个类别都要求出该类的条件概率,然后比较大小得到分类结果。对于给定的输入实例x,分别求得P(Y=1|x)和P(Y=0|x),比较两个条件概率值的大小,将实例x划分到概率值较大的类中。而感知机、决策树是直接得到类别。
接下来,从事件发生几率的角度上,看一下逻辑斯谛函数的特殊性。
一个事件发生的几率是指该事件发生的概率与不发生的概率的比值,如果事件发生的概率是p,那么该事件的几率是p/(1-p),其对数几率或logit函数是:
有了对数几率的函数表达形式,我们将二项逻辑回归模型的表达式代入,得到:
可以发现,输入实例x与该实例被判断成Y=1这个类别的对数几率,竟然是线性关系。换句话说,输出Y=1的对数几率是由输入x的线性函数决定的,这就是逻辑回归模型的来源。正如书中所描述的,换一个角度看,考虑对输入x进行分类的线性函数w·x,其值域为实数域。拟合参数w,使输入数据x可以找到一个决策边界,这个边界是由对数几率表现出来的。直观来说,属于正类的数据,通过w的线性变换,得到一个很大的实数值,因此该数据表现为判断是正类的对数几率大。通过公式6.5,可以将w·x的线性函数值转换为概率:
这时候,线性函数w·x的值越接近正无穷,概率值越接近1;w·x的值越接近负无穷,概率值越接近0,这样的模型就是逻辑回归模型。
模型参数估计
根据以上描述,我们拥有了新的分类模型,可以将w·x的线性函数值转化为类别的概率,那么,我们如何找到分类边界呢?也就是说,我们现在拥有了输入x到类别概率的映射模型,可是怎么保证每个隐射关系都是对的呢?通俗点讲,每一个输入实例x,乘参数向量w之后的线性函数值,转化为类别后都能够被正确分类。关键的问题,也就是在w,如何对w进行估计?这里采用极大似然估计。
似然函数很好理解,进行极大似然估计,需要把每个变量出现的概率连乘起来;连乘式里的表达式,中括号分开的两个部分,在同一个实例上,不会同时成立;式一,实例类别yi=1时,左侧中括号内概率成立,右侧值为1;实例类别yi=0时,右侧中括号内概率成立,左侧值为1。通过这一个式子,就把两个类别出现的概率连乘在了一起。
这样,寻找合适w的过程(寻找决策边界)就变成了以对数似然函数为目标的最优化问题,常用的方法是梯度下降法和拟牛顿法。
多项逻辑斯谛回归
涉及到多分类的逻辑回归模型,该部分有待深入思考公式,留到开学后。
最大熵模型
引入
我更喜欢把这部分内容当做原理,说这个模型的具体应用吧,我这个水平还没有发现。但了解过大概思想后,发现这个模型应该在概率模型中处处存在。最大熵最大熵,顾名思义要让熵最大,延续先前的知识,熵是不确定性的度量,最大熵模型也就是要找出熵最大某个物件。学习之前先提出疑问,比如一个简单的问题,从哪里找到熵最大?熵最大的什么?我刚开始看到这个模型的时候,习惯性的向后翻了翻课本,上来就被数学公式吓到了(静下心来发现没必要这样),仔细阅读一遍之后,除了“什么都没看懂”之外,什么都没懂。
所以在开始记录之前,有必要先强调一下,该模型从原理出发,讨论的是一个概率模型的学习准则问题。假设现在我们有一个分类问题(必须是概率模型),比如说逻辑回归进行分类,我们最后通过比较类别的可能性大小,对新实例做出判断。我们的学习过程,是找到合适的w,从而让所有的数据点,能够得到完美的分类。在逻辑回归模型中,我们是通过极大似然估计,来找到合适的w,而现在我们的最大熵模型,反映的是什么呢?
有了刚才的例子,其实我们可以发现,训练集上每一个w代表了一个模型,只不过呢,有的w分类能力很好(最好的被我们用极大似然估计选择了出来);有的呢,分类能力很差,不被我们采纳。本节提到的最大熵模型,就是从满足条件的模型集合中选出熵最大的模型,我们认为这个熵最大的模型就是最好的模型。简单点,就是从一堆w中,运用熵最大原理找出这个最合适,分类能力最强的w。
最大熵原理
最大熵原理认为,学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型,通常用约束条件来确定概率模型的集合。所以,最大熵原理也可以描述成在满足约束条件的模型集合中选取熵最大的模型,该原理是概率模型学习的一个准则。
解读一下这段。首先,我们针对的是类似逻辑回归、朴素贝叶斯这样的概率模型,不是针对感知机这种决策函数模型。其次,熵最大也就是不确定性最大,这好像与我们的目标相悖,毕竟我们是要找到一个明确的分类边界,现在怎么又要找不确定性最大的呢?这里也挺好理解的,我们在什么情况都不知道的处境下,当然不能偏袒任何一个类别,雨露均沾才能损失最小。如果太过于相信其中一个,万一是假的不就一败涂地了嘛,一点后退的余地都没有。不偏袒任何一个类别就意味着谁都不信,每个的可能性一样,这个时候熵最大,这是公知的。另外,在每个类别可能性一样的前提下得到的模型,对给定实例x进行判断,这时某类的概率还能较大,不更能说明x应该属于这类。最后,我们在训练数据集中学习一个模型,怎么可能一点前提条件都不知道!多多少少有一些特征是我们先知道的,或者说是作为已知条件的。我们要学习的模型,就是在已知的这些条件下,找到最合适的分类模型(应用熵最大原理)。
直观的,最大熵原理认为要选择的概率模型首先必须满足已有的事实,即约束条件。在没有更多信息的情况下,那些不确定的部分都是“等可能的”,最大熵原理通过熵的最大化来表示可能性。书中提到,“等可能”不容易操作,而熵则是一个可以优化的数值指标,这里有待思考(好像事实就是这样)。看一下例子:
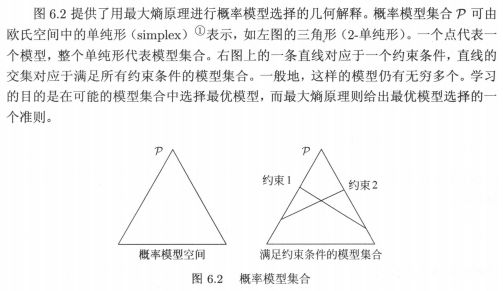
书中又用了一个几何例子解释,正是这个几何例子,放大了对初学者的不友好。看一下书中的解释:
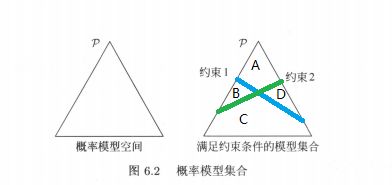
一个点代表一个模型,请问,点在哪里?整个单纯形代表模型集合,请问,是用面积还是边长?直线的交集对应于满足所有约束条件的模型集合,请问,直线与直线相交,难道不是个点吗?最后一句,学习的目的是在可能的模型集合中选择最优模型,最大熵模型则给出最优模型选择的一个准则,拜托,这句话说了多少遍了,和这个几何解释有什么关系?不友好就是不友好,云里雾里的(也可能是我没文化,看不懂数学语言)。可是,如果换一种说法,如下图:
不妨让区域p表示概率模型空间,也就是所有的模型圈在这个三角形区域中(左侧);有一个约束条件,我们就画一条线(右侧蓝绿色直线);约束条件会把模型限制在不同区域(A、B、C、D),约束条件越多,符合条件的模型越少;假设A区域符合约束条件,之前需要从大范围的p区域求最优模型,现在需要在小范围的A区域求解。
最大熵模型的定义
最大熵原理是统计学习的一般原理,应用到分类问题,得到最大熵模型。给出定义前,我们先来思考一下,按照前边描述的思想该模型应该有什么?(1)该模型解决分类问题,要应用在概率模型上,那么我们的目标就应该类似朴素贝叶斯算法,用条件概率分布P(Y|X)表示分类模型。(2)原理部分一直提约束条件,细想一下约束条件可以帮助我们缩小求解范围,的确符合现实意义,可是要怎么找到约束条件呢?留疑。(3)要在所有模型中找到熵最大的模型,用什么熵?衡量模型?(4)如何计算?
带着问题,我们系统性的看一下最大熵模型的定义。首先是分类模型的定义:
分类模型就是我们最后对新数据进行测试的模型,应该是P(Y|X)这个样子。对于一个二分类的新测试实例x,若第一类的条件概率P(y1|x)=0.7,第二类的条件概率P(y2|x)=0.2,有0.7>0.2,我们认为实例x属于第一类。接下来我们寻找约束条件,下述内容(除课本内容外)为个人见解,正确性不能保证。
大胆假设,小心求证,这里我们借鉴一下朴素贝叶斯的东西,来提出约束条件。我们要做的事情,是找到熵最大的分类模型,分类模型是P(Y|X)条件概率分布;朴素贝叶斯是种生成模型,它应用X、Y的联合概率找到生成数据的方式,求解P(Y|X)来计算类别的后验概率;数据集上存在X、Y的联合分布(经验分布);数据集上存在X的分布(经验分布);这里隐约存在一种关系:P(A,B)=P(Y|X)P(X);在数据集固定的情况下,我们已知P(X,Y)、P(X)经验分布,要求的熵最大的条件概率P(Y|X)是不是要满足联合分布规律呢?
答案是一定的,P(A,B)=P(Y|X)P(X)规定了一定存在一个条件概率P(Y|X)分布,使该式成立。现在我们不知道它具体是什么,需要我们求解出来,在求解的过程中,我们猜测的所有条件概率分布,都要满足这个约束才对。
约束条件好像是找到了,现在还差个东西。记得我们在素朴贝叶斯算法中,求过随机变量X和随机变量Y同时出现的联合分布,那时通过极大似然估计对参数求解,事件X和事件Y同时出现这件事,直接计算联合分布了。我们现在的最大熵模型,比较理论化,需要抽象出一个描述联合分布的工具,这个工具不干别的,就是描述数据集中的x、y是否同时存在,是否满足某一事实,是否具有该特征。看一下书中内容:
便于数学形式表达,设计特征函数来表达随机变量X与随机变量Y的取值,同时发生的事实。(这里插一句,在CRF条件随机场中,有个定义在最大团上的势函数,完全可以用来理解这里的特征函数;另外,CRF中的势函数更可以用这里的特征函数来理解;LR和CRF的区别值得好好研究,LR中的W是对特征向量的各个分量进行线性变换,CRF中的W是对定义在最大团上的关联进行线性变换...嘚啵嘚...嘚啵嘚...)
在刚才P(A,B)=P(Y|X)P(X)的描述中,是拿联合分布当做引子,来理解从哪里来的约束条件。在实际的模型,并不是硬性从分布函数相同入手,而是落到具体的数值上(具体的特征上),让期望相等作为模型的约束条件(分布相同,期望相同)。
这里是数据集上联合分布的期望值。
这是数据集上的随机变量X的边缘分布与分类模型P(Y|X)乘积的期望值。
如果分类模型P(Y|X)能够应用到该数据集上,就可以假设P(A,B)=P(Y|X)P(X)公式两边的分布,对特征函数f(x,y)的期望值相等。这样,就可以将公式6.10或公式6.11作为模型学习的约束条件,假设有n个特征函数,相应的就有n个约束条件。
带有约束条件的模型集合我们能够确定了,接下来就是对模型P(Y|X)用什么来度量不确定性,很明显的,用条件熵就可以了。最大熵模型具体定义如下:
该部分还差一点,书中开始部分联合分布P(X,Y)的经验分布和边缘分布P(X)的经验分布如何求?了解朴素贝叶斯算法的同学应该知道,根据大数定律,当训练集包含足够多的样本时,P(X)及P(X,Y)可以通过各事件出现的频率来估计,其中:
最大熵模型的学习
最大熵模型的学习过程就是求解最大熵模型的过程,由公式6.12和公式6.13,求解过程可以形式化为约束最优化问题,即:
按照最优化问题的求解习惯,将求最大值问题改写为等价的求最小值问题:
这里参照书上内容,将约束最优化的原始问题转换为无约束的对偶问题,通过求解对偶问题求解原始问题。
必要的求解过程好像手写一下,标注出关键步骤好像更容易理解,这方面工作开学后会做细致。暂时直接粘贴过来了,仔细看的话,除了对偶问题的转化,其它的计算细节就是微积分了,相信是可以看懂的。
计算过程没什么好解释的,抄一遍实在没什么意思,开学后手写推导一遍,详细写写计算过程。下面看下例子:
极大似然估计
通过原始问题、对偶问题的转换,我们得到了最优的分类模型:由公式6.22、公式6.23表示的条件概率分布。下面内容证明一个等价命题:对偶函数的极大化等价于最大熵模型的极大似然估计。证明过程如下:
一般似然函数是数据集中各个样本的联合概率,本公式给出了似然函数的另一种形式,这个形式需要经过几个步骤的推导,资料已找到,开学整理上手写版本,现在只需要知道该对数似然函数是合理的,将求解的最优分类模型带入似然函数得到:
再看一下对偶函数f(w)化简的结果:
可以发现对偶函数等价于对数似然函数,于是证明了最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计这一事实。
到这里,我们可以得到最大熵模型的一般形式。
查资料的时候,经常看到“最大熵模型与逻辑回归的区别”这个问题,第一遍学完本章内容,脑子里反复思考这两个模型的推导过程,深的浅的有了一些想法,目前尚未形成条理的思路,以后有了,再补上吧。书中说最大熵模型与逻辑回归模型有类似的形式,它们又被称为对数线性模型,这句话是真的没看明白,说逻辑回归是对数线性模型还能理解;可最大熵模型的一般形式,只看到了指数啊,难道是因为求解过程的log,这里存有疑问。
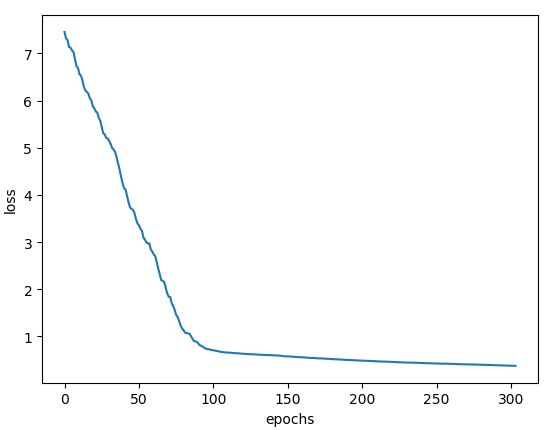
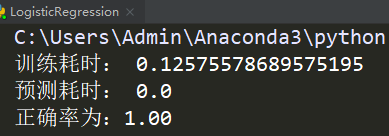
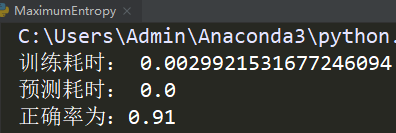
代码效果