神经网络 和 NLP —— 神经网络入门
前段时间一口气读完了 NN4NLP,很是畅快,非常喜欢作者行文讲解的口吻和逻辑。大概两周读完,每页都有收获,读完后反而担心有所疏漏,知识太多留不住,索性从头来一遍,把学习过程的知识点和思考记录下来,也算精简版供自己今后查阅。
感兴趣的,可以一起学习讨论,真的很推荐这本书。
大致介绍下该书。NN4NLP 由 Goldberg 撰写,是 CMU CS11-747 课程的教材,配合公开课食用更佳,公开课链接。本书并非系统介绍 NN 和 NLP,而是聚焦 NN 在 NLP 领域的具体应用,所以分成了四大部分:NN 中前馈神经网络的入门,前馈神经网络在 NLP 中的应用,RNN 等特殊结构在 NLP 中的应用,部分前沿方向介绍。
因此,本博客也打算分成多篇进行总结,其他篇章请自行搜索本博客。
NLP 与 NN 简介
由于人类语言的天然歧义性、不断变化演进、难以确切定义表示支配语言的规则、符号化离散化可组合性稀疏性对计算不友好等特性,使得 NLP 研究极具挑战性。
早期,NLP 的研究停留在符号层面,即基于逻辑、规则和本体。现在,NLP 研究的主流是基于统计的机器学习方法。很长一段时间,核心的 NLP 技术大多是监督学习中的线性模型方法,如感知机、线性 SVM、LR 等。大约从2014年起,NLP 的主流方法转移到非线性的神经网络方法,从而输入也从稀疏高维特征向量变为低位稠密特征向量。
NN 不仅像传统 ML 方法一样学习预测,也学习如何正确表达数据,即在处理输入输出对时,网络内部产生一系列转化以处理输入数据来预测输出数据。设计者需要做的事设计网络结构和训练机制,给网络提供适当的输入输出对,并适当地编码输入数据,繁重的学习正确表达数据的工作由网络完成。
NN 一大优点就是大幅简化了特征工程工作,即允许设计者仅制定一个较小的核心的基本的自然的特征集合,由 NN 结构来将它们组合为更高层级的特征(representation)。也可以说NN最大威力就在于学习到好的 representation 的能力。通常这些 representation很复杂,不单单是线性组合,因此不再具有可解释性。
虽然应用核方法的 ML 算法也可以实现从核心特征中自动结合更高层次的特征,但还是存在缺陷。应用核方法的分类器的计算复杂度和训练数据的规模呈线性关系,因而难以处理大规模数据,而 NN 分类器的计算复杂度只是网络规模的线性关系,和训练数据规模无关。
NN 在 NLP 中的应用,很大一部分涉及嵌入层(embedding layer),即将离散符号应设为连续的低维向量。两大类 NN 结构中,前馈神经网络接收固定尺寸的输入或者变长但不考虑元素顺序的输入,其中 MLP 可以用在任意之前线性模型可用的任务中; RNN 则主要用于处理序列数据,由于避免了之前序列模型中普遍需要的 Markov 假设,大大推广了在语言模型、自动机器翻译等多个 NLP 任务中的应用。当然,RNN 很少作为孤立模块使用,通常作为可训练模块,配合后续网络模块一起使用,主要用来产生向量,喂给后续的预测模块,但训练过程还是 RNN 部分和预测部分一起训练,即 end-to-end。
注意,本书中介绍的 NLP 任务大多是低层次相对定义明确的任务,像对话系统、文档摘要、问答系统等尚属于开放问题的,并未涉及。
神经网络入门
1 从监督机器学习中的线性模型到 MLP
本书所讨论的 NN 是一类监督 ML 算法,因此需要对监督 ML 算法有基本了解,但过于基础,不再细述。
线性模型的限制是处理不了非线性可分问题,典型如 XOR 问题。
一种方法是,手动设计非线性映射,将线性不可分数据转化为线性可分的,通常是变换到更高维空间,再利用线性模型解决。但这个手动设计过程需要靠直觉运气。
一种方法是,利用核技巧,过程同上。但利用核技巧的 SVM 方法将线性依赖训练集的尺寸,使得难以应用到大规模训练数据集。另一个缺点是高维空间增加了过拟合的风险。
另一种方法是,定义一个可训练的非线性映射函数,将其与后续的线性分类器一同训练,即找到合适的映射表示的工作成了训练算法的责任,从而解决非线性可分问题,此即 NN 的主要思想。显然,这个映射函数应可微,从而可以应用基于梯度的训练方法。如下图,
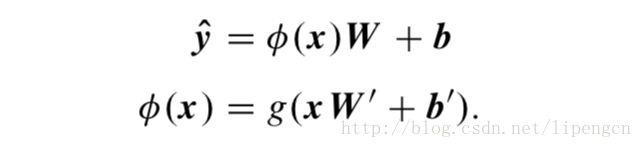
上图即描述了非常常见的 NN 结构——MLP。
2 前馈神经网络
2.1 MLP
典型的前馈神经网络如下图所示,

数学上,可表示为

神经元(Neuron)实现了上一节的φ作用,其中的非线性激活函数实现了 g 的作用。
如果该层所有神经元都与下一层所有神经元相连接,称之为全连接层或者仿射层。
定义了线性映射的项 W 和 b 属于网络的参数,由优化算法学习。给定网络参数,即指定了映射函数;给定网络结构,即指定了映射函数集合。
不过不像线性模型,MLP 的损失函数并不是关于网络参数的凸问题,所以难以获得全局最优解,但仍是使用基于梯度的优化方法去搜寻。
2.2 表现能力
那么 MLP 的表现能力如何呢?Universality Theorem 表明,MLP1 是一个通用逼近器,简单来说可以实现任意的由 N 维实数空间到 M 维实数空间的连续函数。
虽然理论表明一层 MLP 即具有极强的表达能力,但并没告诉我们如何实现这一能力,实际上训练到想要的程度并不简单,包括超参设置。
理论表明,更深的 MLP 比更广的 MLP 性能表现更好。
(1) 从模拟电路角度类比,多层逻辑门来实现某函数更简单些。
(2)从模块化角度来看,不同层实现不同的分类区分功能,越前面实现的分类功能越基础,这样每个基本的分类器也能获得足够的训练样本。
2.3 非线性
非线性 g 有多种形式,目前并没有比较好的理论指导什么样的条件用什么非线性函数更好,通常根据确切任务靠经验选取。
常用的如下:
Sigmoid,σ(x)=1/(1+e^-x)以前较权威,目前在 NN 的内层中已弃用。
Tanh,tanh(x)=(e^2x-1)/(e^2x+1)。
Hard tanh,是 tanh 的近似,但计算和求导更快,hardtanh(x)={-1,x<-1;1,x>1;x,otherwise}。
ReLU,ReLU(x)=max(0,x),虽然形式很简单,但在很多任务中表现不错,尤其是和dropout正则化技术结合时。
2.4 正则化和 dropout
防止 NN 过拟合技术包括正则化和 dropout。
正则化包括 L1、L2和 elastic-net 等,
dropout 设计来避免网络学习着依赖特定权重,可以通过在随机梯度训练中,对每个训练样本随机舍弃网络中或某层的一半神经元(即神经元输出为0)来实现。
理论分析表明,dropout 和 L2 有很强的关联性,此外也可以把 dropout 看做模型平均和 ensemble 技术。
3 NN 的训练
NN 也是可微的参数化函数,可通过基于梯度的优化算法训练。虽然 NN 的非线性导致目标函数非凸,基于梯度的方法很难找到全局最优,但实践中仍然很有效。
线性模型中的梯度计算依赖微分的链式法则,这在复杂网络中变得艰难且易错。乐村98年提的反向传播算法有效地解决了这个问题。
反向传播算法通过缓存中间结果,来计算利用链式法则的复杂表达式的导数。反向传播算法也可以看做反转自动微分算法的特例。
3.1 计算图抽象
计算图抽象可以方便实现:构建任意网络、估计对应输入的预测(前向传导)、关于任意标量损失计算参数的梯度(反向传导)。
计算图将任意数学计算表述为一个图,是一个有向无环图(DAG)。NN 也是一个数学表达式,因此可以表示成计算图,如 MLP1 可以表示为

通常计算图的构造通过已有的软件库或者 API 完成,之后只要直接执行前向计算获得计算结果,或者反向计算获得梯度即可。
(1) 前向计算

注意,这里的 N 个节点的序号 i 由拓扑排序确定,DAG 拓扑排序的经典算法由 khan、DFS 等。
(2) 反向计算
(3) 实现软件
实现计算图模型的软件包有不少,包括 Theano、TensorFlow、Chainer、DyNet 等。
DyNet 和 Chainer 使用的动态图构建方式,TensorFlow 和 Theano 采用了静态图构建方式。
在动态图构建方式中,每次对训练样本通过语言编码重新产生一个不同的计算图,然后前向和方向传播应用于该图。在静态图构建方式中,计算图的形状通过 API 在计算最初只定义一次,然后优化图编译器会产生一个最优的计算图,每个训练样本都将喂给这个最优计算图。
静态图构建方式是把双刃剑。一方面,一旦构建就可以在 CPU 或 GPU 上高效运行,特别适合固定结构的大型图。另一方面,编译过程本身非常耗时,使得接口更难应用。此外,对于 RNN 和在结构化预测环境中,动态图构建方式更方便。
4 实践考量
4.1 训练结果不理想时
(1)选择合适的损失函数
当使用 softmax 输出层时,选择交叉熵,而非平方和。
(2)Mini-batch
有时大点的 minibatch 计算效率更高,如 GPU 上。
(3)尝试新的激活函数
早期的 sigmoid 容易产生梯度消失问题,15年开始采用 ReLU及其变种。
ReLU 属于 MaxOut 的特例。
(4)自适应学习速率
学习速率通常从0.001、0.01、0.1、1中进行试验。一般学习速率应随着训练进行递减。
注意,learning rate cannot be one-size-fits-all, and give different parameters different learning rate。
AdaGrad、AdaDelta、RMSProp、Adam 等,属于自适应学习速率算法。通常,对于大规模网络,Adam 表现更高效也更强健。
(5)添加动量
SGD+Momentum,Nesterov Momentum 等,属于SGD 的变种,将前面的梯度进行累积影响本次更新。
(6)shuffling
训练样本供给给网络的顺序也很重要。一般建议提前 shuffle 数据。但当样本不是 IID 时,shuffle 反而不合适。
每个 epoch 采用的训练数据都要 shuffle,通常软件包自行处理了,如 keras。
4.2 测试结果不理想时:
(1)早点停止迭代
早点停止训练,避免过拟合。
(2)衰减权重(属于正则化)
更新公式中,在 w 前乘以一个0.99之类的,让 w 越来越小。从而修剪掉无用的权重。
(3)dropout(属于正则化)
训练时,每个 mini-batch 对隐层神经元随机删除 p%后进行训练。此时,每次实际上训练了不同的网络结构,且更 thinner。可以看出,采用 dropout 也可以看做采用了 ensemble。
测试时,不必 dropout,每个训练好的权重乘以 (1-p)%即可。
当前Dropout大量应用于全连接网络,而且一般人为设置为0.5或者0.3,经过交叉验证,隐含节点dropout率等于0.5的时候效果最好,原因是0.5的时候dropout随机生成的网络结构最多。
而在卷积隐藏层由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积隐藏层中使用较少。
(4)L1 L2 正则化
(5)调整网络结构
4.3 其他
(1)梯度消失
梯度消失,即权重不再更新,本质是反向传播时,链式法则连乘造成的,即每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话,在经过足够多层传播之后,误差对输入层的偏导会趋于0。
主要是因为以前用sigmoid的时候,sigmoid中心部位和两侧的梯度差别太大,如果权重初始化得太大,激活值基本都在sigmoid两侧,两侧梯度几乎为0,传播几层就没有梯度了。sigmoid 函数的导数最大为1/4,即使用很好的初始化算法把激活值控制在一个合理范围内,优化几下有几个神经元就又跑到两侧了,而一旦到两侧,因为梯度过小,就再也无法通过梯度更新来使其恢复。
这个问题在提出ReLU和有效的初始化方法(例如MSRA)后已经大概率解决。后来又出了个Batch Normalization,不管优化多少层都跟浅层一样,梯度消失问题基本可以认为彻底解决了。
A. ReLU 类激活函数
当激活函数的导数为1,那么就不存在梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度。
B. Batch-norm
批规范化,通过规范化操作将每一层的输出信号,规范化到均值为0,方差为1,消除了w带来的放大缩小的影响,进而解决梯度消失和爆炸的问题,保证网络的稳定性。
反向传播时经过该层的梯度是要乘以该层的参数的,即前向有:h_l = w_l^T*h_{l-1},反向传播时有:
\frac{\partial l}{\partial h_{l-1}} = \frac{\partial l}{\partial h_l} . \frac{\partial h_l}{\partial h_{l-1}} = \frac{\partial l}{\partial h_l} w_l。
BN作用是抹去了w的scale影响,避免了梯度消失和爆炸。
C. 残差结构
D. 浅化网络
E. LSTM 等门结构网络
通过门结构控制,避免梯度消失。
(2)梯度爆炸
梯度爆炸,产生机制同梯度消失。在极端情况下,权重的值变得非常大,以至于溢出,导致 NaN 值。
处理梯度爆炸,简单但有效的方式即当梯度的范数超过某阈值时修剪该梯度。其次,ReLU、Batch-norm、浅化网络、LSTM 等方法也都有效。
(3)饱和及死亡神经元
采用 tanh 和 sigmoid 激活函数的层可能出现饱和现象,即该层的输出值均接近1(激活函数的上限),导致该层的梯度非常小。
进入该层的值太大将导致饱和神经元出现。
改变初始化方式、缩放输入值的范围、改变学习率等方式可能起到控制作用。对于饱和层,还有一种选择是归一化饱和层经过激活函数后输出的值,该方法虽然对计数饱和有效,但计算复杂度高。CV 中还有一种相关的技术较批正则化,只是 NLP 中应用很少。
采用 ReLUctant 激活函数的层虽不会饱和,但可能死亡,即绝大多数输出值为负因此对所有输入都被修剪为0,导致该层的梯度为0。
进入该层的所有值均为负将导致死亡神经元出现。
降低学习率将会有所帮助。
(4)初始化
随机值的量级对训练影响也很大。
通常采用 bengio2010 提出的 xavier 初始化方法。许多环境会默认选择此方法。He2015提出使用 ReLU 时,从零均值 sqrt(2/d_in) 标准差高斯分布取样进行初始化性能也很好,尤其适用于深度网络。
来看下xavier方法,为了使得网络中信息更好的流动,每一层输出的方差应该尽量相等。基于这个目标,推导出每一层的权重应该满足哪种条件,这种条件就是 xavier 方法的核心。
为了保证前向传播和反向传播时每一层的方差一致,应满足:

其中 n_i 是输入个数,n_i+1是输出个数。
但是,实际当中输入与输出的个数往往不相等,于是为了均衡考量,最终我们的权重方差应满足:

因此,Xavier初始化的实现就是满足下面的均匀分布: