2020 hdu contest 1 (水题)
自我感觉航电的题目极其经典
Distinct Sub-palindromes
Problem Description
S is a string of length n. S consists of lowercase English alphabets.
Your task is to count the number of different S with the minimum number of distinct sub-palindromes. Sub-palindrome is a palindromic substring.
Two sub-palindromes u and v are distinct if their lengths are different or for some i (0≤i≤length), ui≠vi. For example, string “aaaa” contains only 4 distinct sub-palindromes which are “a”, “aa”, “aaa” and “aaaa”.
Input
The first line contains an integer T (1≤T≤105), denoting the number of test cases.
The only line of each test case contains an integer n (1≤n≤109).
Output
For each test case, output a single line containing the number of different strings with minimum number of distinct sub-palindromes.
Since the answer can be huge, output it modulo 998244353.
Sample Input
2
1
2
Sample Output
26
676
第一个最简单的题目,有多少种可能的字符串里面包含的回文串最小,枚举一下发现,n = 1的时候,回文串的数量是1,有26种字符串,n = 2 , 3的时候,不管有几个字母 是相同,回文串的数量都是3,当n大于3的时候,我们也可以构造出只有3个回文串的字符串,只要abcabcabc的构造就行了, 这个有26 * 25 * 24个
#include
#include Fibonacci Sum
Since the answer can be huge, output it modulo 1000000009 (109+9).
求解这个公式
写在这个地方,纪念第一次遇到这种题目
斐波拉契数列的通项公式:
f [ i ] = a f [ i − 1 ] + b ∗ f [ i − 2 ] f [ n ] = k n ∗ ( f [ 1 ] − m ∗ f [ 0 ] ) − m n ∗ ( f [ 1 ] − k ∗ f [ 0 ] ) k − m m = a + a 2 + 4 b 2 k = a − a 2 + 4 b 2 f[i] = af[i - 1] + b * f[i - 2] \\ f[n] = \frac{k^n*(f[1]-m*f[0]) - m^n*(f[1] -k* f[0])}{k - m} \\ m = \frac{a +\sqrt{a^2+4b}}{2} \\ k = \frac{a -\sqrt{a^2+4b}}{2} f[i]=af[i−1]+b∗f[i−2]f[n]=k−mkn∗(f[1]−m∗f[0])−mn∗(f[1]−k∗f[0])m=2a+a2+4bk=2a−a2+4b
由此得出当前公式的斐波拉契数列通项公式
f n = 1 5 ∗ { ( 1 + 5 2 ) n − ( 1 − 5 2 ) n } f 0 = 0 , f 1 = 1 f_n = \frac{1}{\sqrt5} * \{{(\frac{1 + \sqrt5}{2}) ^ n - (\frac{1 - \sqrt5}{2})^n}\} \\ f_0 = 0 , f_1 = 1 fn=51∗{(21+5)n−(21−5)n}f0=0,f1=1
在模意义下, 5 \sqrt5 5是可以求出来的,根据二次剩余定理 x 2 = 5 % m o d x^2 =5 \% mod x2=5%mod
template<typename T>
inline int pow(int x,T y)
{
rg int res=1;x%=mod;
for(;y;y>>=1,x=(ll)x*x%mod)if(y&1)res=(ll)res*x%mod;
return res;
}
inline int Quadratic_residue(const int a)
{
if(a==0)return 0;
int b=(rand()<<14^rand())%mod;
while(pow(b,(mod-1)>>1)!=mod-1)b=(rand()<<14^rand())%mod;
int s=mod-1,t=0,x,inv=pow(a,mod-2),f=1;
while(!(s&1))s>>=1,t++,f<<=1;
t--,x=pow(a,(s+1)>>1),f>>=1;
while(t)
{
f>>=1;
if(pow((int)((ll)inv*x%mod*x%mod),f)!=1)x=(ll)x*pow(b,s)%mod;
t--,s<<=1;
}
return min(x,mod-x);
}
先把 5 \sqrt5 5求解出来之后,剩下的都可以用费马小定理求解在模意义下的逆元,D = 1 5 % m o d \frac{1}{\sqrt5} \% mod 51%mod , A = 1 + 5 2 % m o d \frac{1 + \sqrt5}{2}\%mod 21+5%mod , B = 1 − 5 2 % m o d \frac{1 - \sqrt5}{2}\%mod 21−5%mod
f n k = D k ∗ ( A n − B n ) k f_n ^k= D ^ k * (A^n - B ^n)^k fnk=Dk∗(An−Bn)k
下面就是新学到的小技巧,虽然高中都学过,经常用,但是这个时候却想不起来,太失败了:后面是一个二项式,直接展开
f n k = D k ∗ [ C k 0 ∗ ( A n ) k ∗ ( B n ) 0 ∗ ( − 1 ) 0 + C k 1 ∗ ( A n ) k − 1 ∗ ( B n ) 1 ∗ ( − 1 ) 1 + . . . . . . + C k k ∗ ( A n ) 0 ∗ ( B n ) k ∗ ( − 1 ) k ] f_n^k = D^k*[C_k^0 * (A^n)^k * (B^n)^0*(-1)^0 +C_k^1 * (A^n)^{k -1} * (B^n)^1*(-1)^1 + ......+ C_k^k * (A^n)^0 * (B^n)^k*(-1)^k] \\ fnk=Dk∗[Ck0∗(An)k∗(Bn)0∗(−1)0+Ck1∗(An)k−1∗(Bn)1∗(−1)1+......+Ckk∗(An)0∗(Bn)k∗(−1)k] f 2 n k = D k ∗ [ C k 0 ∗ ( A 2 n ) k ∗ ( B 2 n ) 0 ∗ ( − 1 ) 0 + C k 1 ∗ ( A 2 n ) k − 1 ∗ ( B 2 n ) 1 ∗ ( − 1 ) 1 + . . . . . . + C k k ∗ ( A 2 n ) 0 ∗ ( B 2 n ) k ∗ ( − 1 ) k ] f_{2n}^k = D^k*[C_k^0 * (A^{2n})^k * (B^{2n})^0*(-1)^0 +C_k^1 * (A^{2n})^{k -1} * (B^{2n})^1*(-1)^1 + ......+ C_k^k * (A^{2n})^0 * (B^{2n})^k*(-1)^k] \\ f2nk=Dk∗[Ck0∗(A2n)k∗(B2n)0∗(−1)0+Ck1∗(A2n)k−1∗(B2n)1∗(−1)1+......+Ckk∗(A2n)0∗(B2n)k∗(−1)k] = D k ∗ [ C k 0 ∗ ( A n ) 2 k ∗ ( B n ) 2 ∗ 0 ∗ ( − 1 ) 0 + C k 1 ∗ ( A n ) 2 ( k − 1 ) ∗ ( B n ) 2 ∗ ( − 1 ) 1 + . . . . . . + C k k ∗ ( A n ) 2 ∗ 0 ∗ ( B n ) 2 k ∗ ( − 1 ) k ] =D^k*[C_k^0 * (A^n)^{2k} * (B^n)^{2*0}*(-1)^0 +C_k^1 * (A^n)^{2(k -1)} * (B^n)^2*(-1)^1 + ......+ C_k^k * (A^n)^{2*0} * (B^n)^{2k}*(-1)^k] \\ =Dk∗[Ck0∗(An)2k∗(Bn)2∗0∗(−1)0+Ck1∗(An)2(k−1)∗(Bn)2∗(−1)1+......+Ckk∗(An)2∗0∗(Bn)2k∗(−1)k] f 3 n k = D k ∗ [ C k 0 ∗ ( A n ) 3 ∗ k ∗ ( B n ) 0 ∗ ( − 1 ) 3 ∗ 0 + C k 1 ∗ ( A n ) 3 ( k − 1 ) ∗ ( B n ) 3 ∗ ( − 1 ) 1 + . . . . . . + C k k ∗ ( A n ) 3 ∗ 0 ∗ ( B n ) 3 ∗ k ∗ ( − 1 ) k ] f_{3n}^k = D^k*[C_k^0 * (A^{n})^{3 * k} * (B^{n})^0*(-1)^{3 * 0} +C_k^1 * (A^{n})^{3(k -1)} * (B^{n})^3*(-1)^1 + ......+ C_k^k * (A^{n})^{3 * 0} * (B^{n})^{3 * k}*(-1)^k] \\ f3nk=Dk∗[Ck0∗(An)3∗k∗(Bn)0∗(−1)3∗0+Ck1∗(An)3(k−1)∗(Bn)3∗(−1)1+......+Ckk∗(An)3∗0∗(Bn)3∗k∗(−1)k]
优化:
- 发现 D k D^k Dk 这个系数不论n为多少,都不变,所以我们最后乘一下就行
- 枚举 C k r C_k^r Ckr , 那么对于同一个r而言, f c + f 2 c + . . . . + f n c f_c+f_{2c}+....+f_{nc} fc+f2c+....+fnc其中 C k r C_k^r Ckr项的贡献是一个等数列,首项和公比都是 q = ( A n ) k − r ∗ ( B n ) r q = (A^n)^{k - r} * (B^n)^{r} q=(An)k−r∗(Bn)r , 并且从枚举r到枚举r + 1 , 公比q的变化为 q = q ∗ B n ( A n ) q = \frac{q * B^n}{(A^n)} q=(An)q∗Bn , 与处理一下就行了。
- 还要特判公比q = 1的情况,此时 f c + f 2 c + . . . . + f n c f_c+f_{2c}+....+f_{nc} fc+f2c+....+fnc其中 C k r C_k^r Ckr项的贡献是 n
#include
#include Finding a MEX
Problem Description
Given an undirected graph G=(V,E). All vertices are numbered from 1 to N. And every vertex u has a value of Au. Let Su={Av│(u,v)∈E}. Also, F(u) equals MEX(minimum excludant) value of Su. A MEX value of a set is the smallest non-negative integer which doesn’t exist in the set.
There are two types of queries.
Type 1: 1 u x – Change Au to x (0≤x≤109).
Type 2: 2 u – Calculate the value of F(u).
For each query of type 2, you should answer the query.
Input
The first line of input contains a single integer T (1≤T≤10) denoting the number of test cases. Each test case begins with a single line containing two integers n (1≤n≤105), m (1≤m≤105) denoting the number of vertices and number of edges in the given graph.
The next line contains n integers and ith of them is a value of Ai (0≤Ai≤109).
The next m lines contain edges of the graph. Every line contains two integers u, v meaning there exist an edge between vertex u and v.
The next line contains a single integer q (1≤q≤105) denoting the number of queries.
The next q lines contain queries described in the description.
Output
For each query of type 2, output the value of F(u) in a single line.
Sample Input
1
5 4
0 1 2 0 1
1 2
1 3
2 4
2 5
5
2 2
1 2 2
2 2
1 3 1
2 1
Sample Output
2
2
0
1. 首先对于一个维护mex值,可以直接for循环扫一遍,或者用权值线段树或者树状数组加二分查询,如果数据小的话,就可以直接用for循环扫一遍,数据大的话,需要树状数组加二分了
2. 对于一点图里面的点而言,如果它的邻接点而言,如果数量很少,就可以直接使用第一种情况求mex,否则的话,需要第二种情况求mex
3. 在本题,取 n \sqrt{n} n为数据大小的分界点
4. 如果一个点u的度数为d[u] , 那么他的mex值最多最多只有d[u] 个, 0 , 1 , 2 , 3 , 4 5.。。。。d[u] , 所以只要在求解mex的时候,碰到点的权值 a [ u ] > = d [ u ] a[u] >= d[u] a[u]>=d[u] , 那么这点可以不做处理。
5. 对于本题种第一种方法求解mex,直接扫一遍临点即可。
6. 对于第二种方法,用树状数组的话,将每个大节点建立一个树状数组,不过空间要求下, 需要动态开点,用个vector动态开点即可, 将a[x] = w , 只需要先删除这个a[x] , 然后再插入w, 更新对临点的影响, 在临点的树状数组上面操作,查询的话就二分查找一下即可
#include
#include Leading Robots
Problem Description
Sandy likes to play with robots. He is going to organize a running competition between his robots. And he is going to give some presents to the winners. Robots are arranged in a line. They have their initial position (distance from the start line) and acceleration speed. These values might be different. When the competition starts, all robots move to the right with speed:
Here a is acceleration speed and t is time from starting moment.
Now, the problem is that, how many robots can be the leader from the starting moment?
Here leader means the unique rightmost robot from the start line at some moment. That is, at some specific time, if a robot is rightmost and unique then it is the leading robot at that time. There can be robots with same initial position and same acceleration speed.
The runway is so long that you can assume there’s no finish line.
Input
The input consists of several test cases. The first line of input consists of an integer T(1≤ T≤50), indicating the number of test cases. The first line of each test case consists of an integer N(0 < N≤ 50000), indicating the number of robots. Each of the following N lines consist of two integers: p,a (0 < p,a < 231) indicating a robot’s position and its acceleration speed.
Output
For each test case, output the number of possible leading robots on a separate line.
Sample Input
1
3
1 1
2 3
3 2
Sample Output
2
根据物理学公式 x = x 0 + a t 2 2 x = x_0 + \frac{at^2}{2} x=x0+2at2 , 转化为 y = k ∗ x + b b = 2 ∗ x 0 k = a y = k * x + b \\ b = 2 * x_0 \\ k = a y=k∗x+bb=2∗x0k=a
题目要求有多少种情况有一个人领先,看这写直线组成的直线图
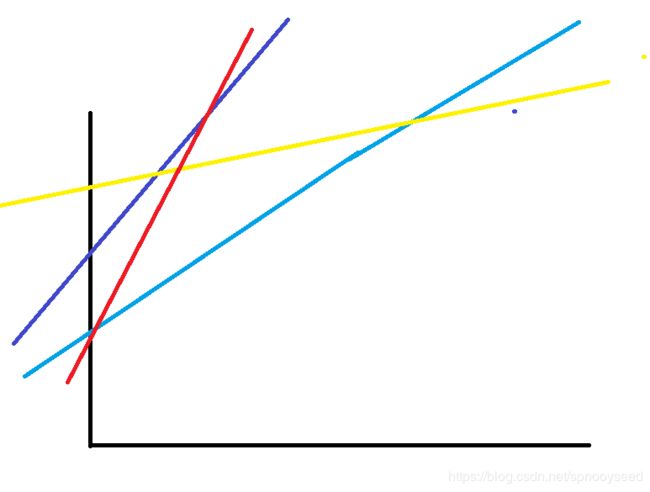
题目也就是要求有多少直线在最上面,可以发现
- 如果当前直线的斜率和初始位置都大于另一条直线,那么肯定选当前直线
- 如果当前直线存在重复的几条,那么肯定没戏
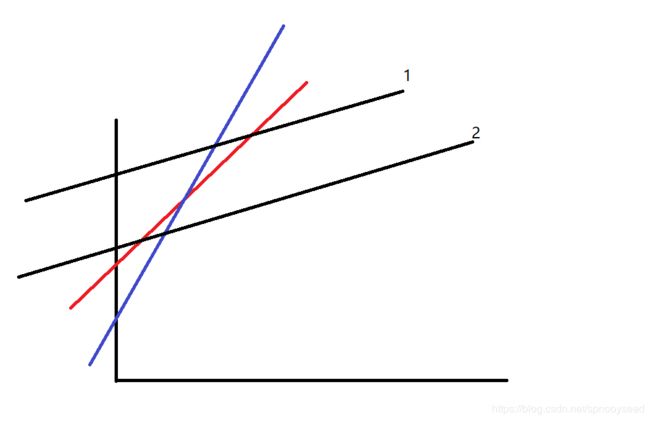
- 对于排除上面两个条件,基本上就只剩下上图中的关系,黑色的线是两种情况,蓝色和红色是固定的,那么总共两种情况,可以发现对于2号黑色的线来说,三条线都有可能,但是对于1号线来说,红色的线完全没戏。
4.怎么判断1号线和2号线呢,用一个栈维护,首先排掉前两种条件,然后看两条黑色线的与蓝色与红色线的交点即可
#include
#include