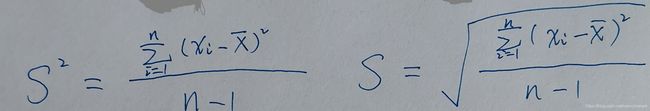机器学习学习笔记(12)----特征缩放
在《机器学习学习笔记(11)----测试softmax回归》文章中,在对softmax模型进行训练时,我们使用了特征缩放技术。使用特征缩放来处理训练数据集的主要原因是:我在使用原始数据进行训练时发现,进行梯度下降迭代时,损失函数不收敛,无法达到训练效果,所以只好采用特征缩放技术对数据进行处理后再尝试,然后发现取得了良好效果。
上篇文章对特征缩放的描述比较简单,本文准备总结整理一下。
首先介绍几个术语:
1,方差和标准差:
1)设总体的方差为![]() ,标准差为
,标准差为![]() ,对于未分组整理的原始数据,方差和标准差的计算公式分别为:
,对于未分组整理的原始数据,方差和标准差的计算公式分别为:
其中![]() 是Xi的算术平均值。
是Xi的算术平均值。
2)设样本的方差为![]() ,标准差为S,对于未分组整理的原始数据,方差和标准差的计算公式分别为:
,标准差为S,对于未分组整理的原始数据,方差和标准差的计算公式分别为:
其中![]() 是xi的算术平均值。
是xi的算术平均值。
2,范数
对于n维实数空间![]() 中,有向量:,则
中,有向量:,则
![]()
称为向量![]() 的
的![]() 范数。
范数。
机器学习的几种特征缩放的方法:
1,min-max缩放
使用min-max缩放将各特征值缩放到[0,1]区间:
2,标准化(Standardization)
3,![]() 范数归一化
范数归一化
Scikit-Learn库使用示例:
1,min-max缩放
>>> import numpy as np
>>> from sklearn.preprocessing import MinMaxScaler
>>> a = np.array([[1,2,3,4],[4,5,6,7],[7,8,9,10]])
>>> mm = MinMaxScaler()
>>> a_mm = mm.fit_transform(a)
>>> a_mm
array([[0. , 0. , 0. , 0. ],
[0.5, 0.5, 0.5, 0.5],
[1. , 1. , 1. , 1. ]])
为什么是这样的结果呢?
按照《sklearn.preprocessing.MinMaxScaler》(http://lijiancheng0614.github.io/scikit-learn/modules/generated/sklearn.preprocessing.MinMaxScaler.html),MinMaxScaler是这样计算的:
a_std = (a - a.min(axis=0)) / (a.max(axis=0) - a.min(axis=0))
a_scaled = a_std * (max - min) + min
如果不显示指定,默认的max值是1,min值是0。
以第一列为例,对各个行取最小值是1,最大值是7,那么按照公式算得![]() 。
。
2,标准化(Standardization)
>>> from sklearn.preprocessing import StandardScaler
>>> ss = StandardScaler()
>>> a_ss = ss.fit_transform(a)
>>> a_ss
array([[-1.22474487, -1.22474487, -1.22474487, -1.22474487],
[ 0. , 0. , 0. , 0. ],
[ 1.22474487, 1.22474487, 1.22474487, 1.22474487]])
从这个计算结果可以看出,StandardScaler使用的计算方差和标准差的公式,应该是总体的方差和标准差的计算公式,而不是样本的方差和标准差计算公式。
3, ![]() 范数归一化
范数归一化
>>> from sklearn.preprocessing import Normalizer
>>> nm = Normalizer()
>>> a_nm = nm.fit_transform(a)
>>> a_nm
array([[0.18257419, 0.36514837, 0.54772256, 0.73029674],
[0.35634832, 0.4454354 , 0.53452248, 0.62360956],
[0.40824829, 0.46656947, 0.52489066, 0.58321184]])
注意:前两个特征缩放都是针对行进行处理,但是这个是针对列进行处理。
参考资料:
《Python机器学习算法与应用》
《精通特征工程》
《机器学习基础教程》
《sklearn.preprocessing.MinMaxScaler》(http://lijiancheng0614.github.io/scikit-learn/modules/generated/sklearn.preprocessing.MinMaxScaler.html)