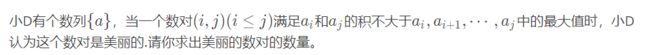洛谷 P4755 Beautiful Pair —— 主席树+笛卡尔树

This way

题意：

题解：

这道题就比2020牛客三的题目简单很多了，我一眼就看出来他是主席树+笛卡尔树。但是我觉得这道题应该有时间复杂度更低的做法，等有时间了再琢磨琢磨。
那么首先以下标为顺序，值越大优先级越高的形式建立笛卡尔树。
然后再dfs这棵树。
此时的时间复杂度是$O(n)$的，那我就在想，是否可以对于每个区间都快速$O(1)$或者$O(log)$得到。
我一下子想不出来
然后我就想到了枚举当前区间较短的一边，这样时间复杂度最多是$O(log)$的，然后枚举每个数的时候，查询另一边有多少数<=a[root]/a[p]。那么此时可以用主席树$O(log)$查询。所以总的时间是$O(nlo{g}^{2}n)$

#include
using namespace std;
#define ll long long
const int N=1e5+5;
int ls[N],rs[N],fa[N],st[N],top,a[N],b[N];
int n;
struct Chairman{
    int ls[N*40],rs[N*40],rt[N],num[N*40],tot;
    void build(){
        for(int i=1;i<=n;i++)
            update(1,n,rt[i]=++tot,rt[i-1],a[i]);
    }
    void update(int l,int r,int root,int last,int p){
        ls[root]=ls[last];
        rs[root]=rs[last];
        num[root]=num[last]+1;
        if(l==r)return ;
        int mid=l+r>>1;
        if(mid>=p)
            update(l,mid,ls[root]=++tot,ls[last],p);
        else
            update(mid+1,r,rs[root]=++tot,rs[last],p);
    }
    int query(int l,int r,int root,int last,int ql,int qr){
        if(l>=ql&&r<=qr)
            return num[root]-num[last];
        int mid=l+r>>1;
        int ans=0;
        if(mid>=ql)
            ans=query(l,mid,ls[root],ls[last],ql,qr);
        if(mid<qr)
            ans+=query(mid+1,r,rs[root],rs[last],ql,qr);
        return ans;
    }
}t;
void build(){
    for(int i=1;i<=n;i++){
        while(top&&a[st[top]]<a[i])
            ls[i]=st[top--];
        fa[i]=st[top];
        if(ls[i])fa[ls[i]]=i;
        if(fa[i])rs[fa[i]]=i;
        st[++top]=i;
    }
}
ll ans=0;
int all;
void dfs(int l,int r,int root){
    if(l==r){
        ans+=b[a[l]]==1;
        return ;
    }
    if(root-l<=r-root){
        for(int i=l;i<=root;i++){
            int v=b[a[root]]/b[a[i]];
            int p=upper_bound(b+1,b+1+all,v)-b-1;
            if(p)
                ans+=t.query(1,n,t.rt[r],t.rt[root-1],1,p);
        }
    }
    else{
        for(int i=root;i<=r;i++){
            int v=b[a[root]]/b[a[i]];
            int p=upper_bound(b+1,b+1+all,v)-b-1;
            if(p)
                ans+=t.query(1,n,t.rt[root],t.rt[l-1],1,p);
        }
    }
    if(ls[root])dfs(l,root-1,ls[root]);
    if(rs[root])dfs(root+1,r,rs[root]);
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),b[i]=a[i];
    sort(b+1,b+1+n);
    all=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;i++)
        a[i]=lower_bound(b+1,b+1+all,a[i])-b;
    t.build();
    build();
    dfs(1,n,st[1]);
    printf("%lld\n",ans);
    return 0;
}